
- •Технический университет – упи», 2005
- •Введение Основные понятия
- •Линейные дифференциальные уравнения высшего порядка
- •Решения задания типового варианта
- •4. Решить начальную задачу Коши
- •Ответ: .
- •12. Найти общее решение уравнения
- •V. 17. Последнее задание содержит задачи двух типов – составление и решение дифференциального уравнения на физическую и геометрическую тему. Рассмотрим оба типа задач.
Решения задания типового варианта
I. Первые семь уравнений являются дифференциальными уравнениями первого порядка. Среди них представлены уравнения: с разделяющимися переменными, однородные, линейные, уравнения Бернулли и в полных дифференциалах.
1. Найти общее решение (общий интеграл) уравнения
![]() .
.
Решение. Для установления типа дифференциального уравнения преобразуем его, применив формулу разности синусов:
![]() – получилось
уравнение
с разделяющимися переменными.
– получилось
уравнение
с разделяющимися переменными.
Метод решения.
Заменим производную отношением
дифференциалов
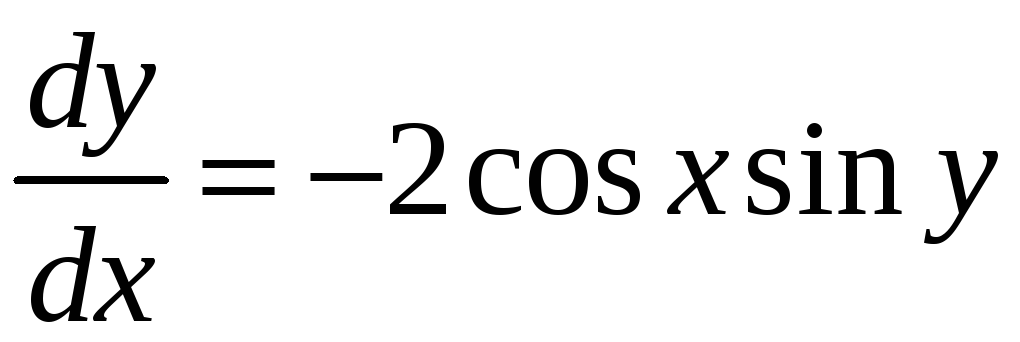 и разделим
переменные:
и разделим
переменные:
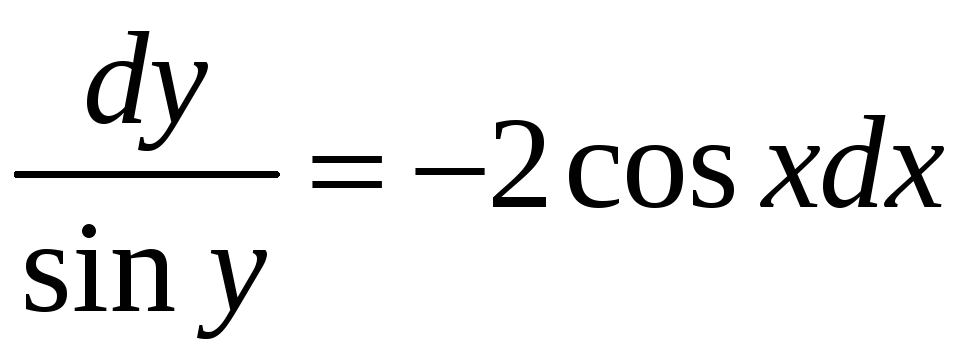 .
Далее проинтегрируем обе части полученного
уравнения:
.
Далее проинтегрируем обе части полученного
уравнения:
 ,
,
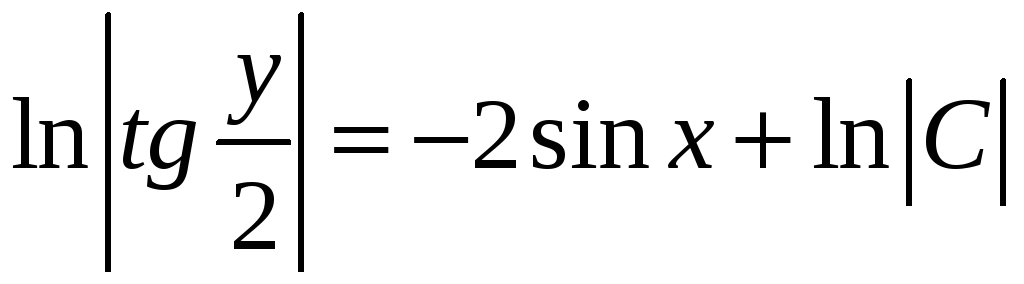 .
Получим общее
решение исходного уравнения
.
Получим общее
решение исходного уравнения
![]() .
.
Ответ:
Общее решение
![]() .
.
2. Решить начальную задачу Коши
![]() ,
,
![]() .
.
Решение. Сначала найдём общий интеграл этого уравнения. Преобразовав уравнение, сведём его к уравнению с разделяющимися переменными:
![]() ,
,
 .
.
Проинтегрируем обе части полученного уравнения:
 ,
,
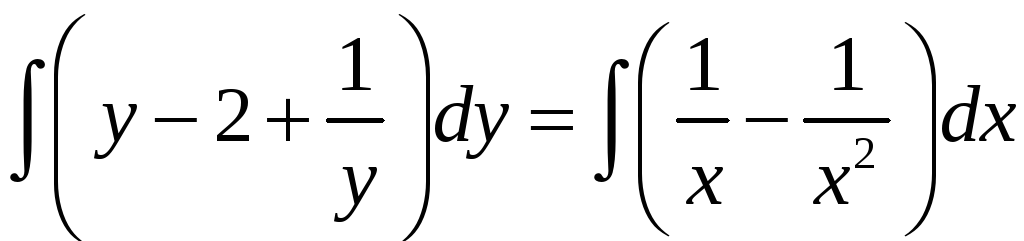 ,
,
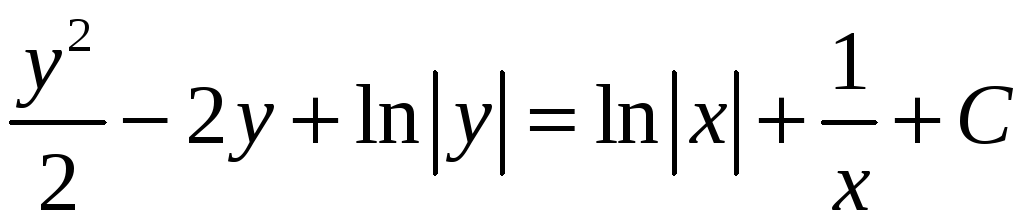 – получили общий
интеграл. Теперь найдём значение
произвольной постоянной С,
подставив в общий интеграл исходные
начальные условия
– получили общий
интеграл. Теперь найдём значение
произвольной постоянной С,
подставив в общий интеграл исходные
начальные условия
![]() :
:
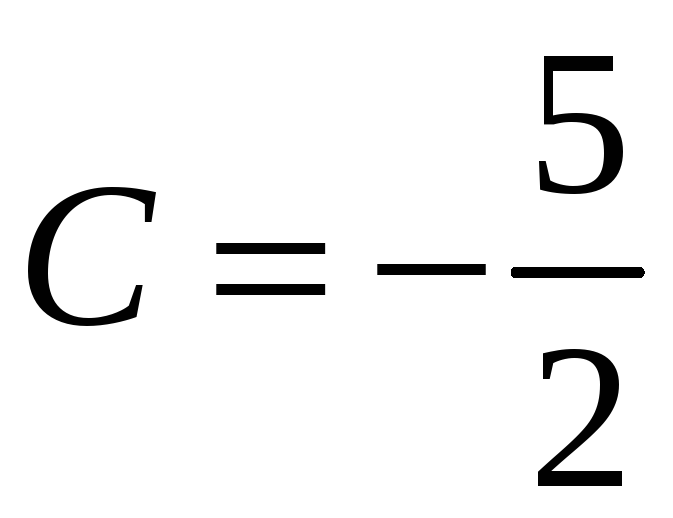 .
Таким образом,
частное решение (частный интеграл)
исходного уравнения, удовлетворяющее
заданным начальным условиям, имеет вид
.
Таким образом,
частное решение (частный интеграл)
исходного уравнения, удовлетворяющее
заданным начальным условиям, имеет вид
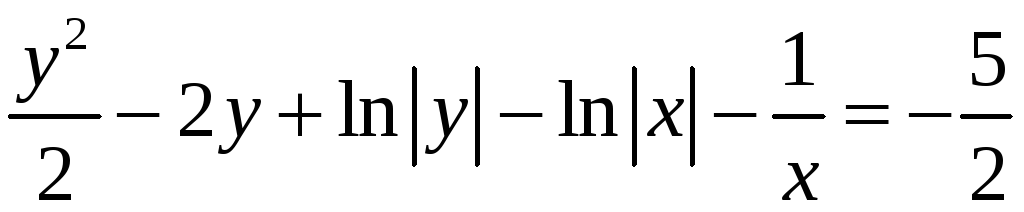
Ответ:
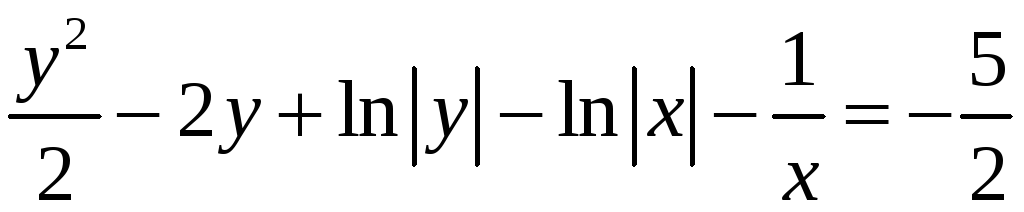 .
.
3. Найти общий интеграл уравнения
![]() .
.
Решение. Разрешим уравнение относительно производной:
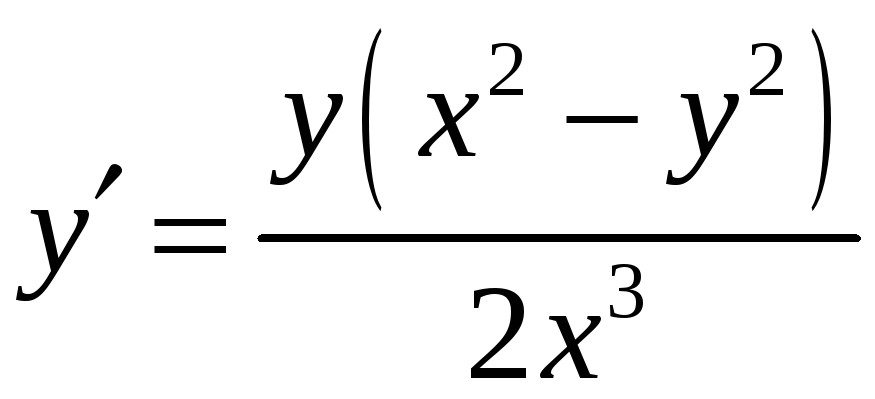 ,
,
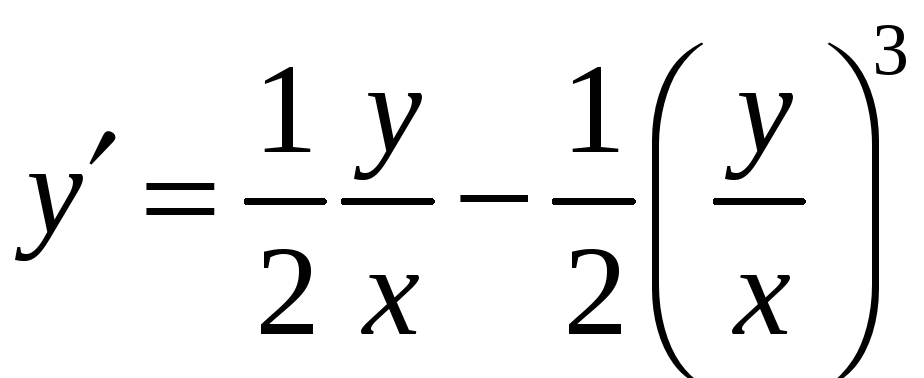 -
получилось однородное
уравнение.
Метод решения.
Сделаем замену и перейдём к уравнению
относительно новой функции:
-
получилось однородное
уравнение.
Метод решения.
Сделаем замену и перейдём к уравнению
относительно новой функции:
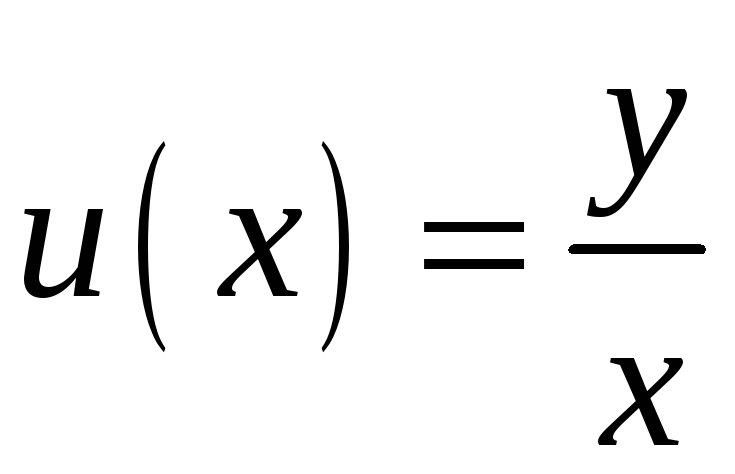 ,
,
![]() ,
,
![]() ,
,
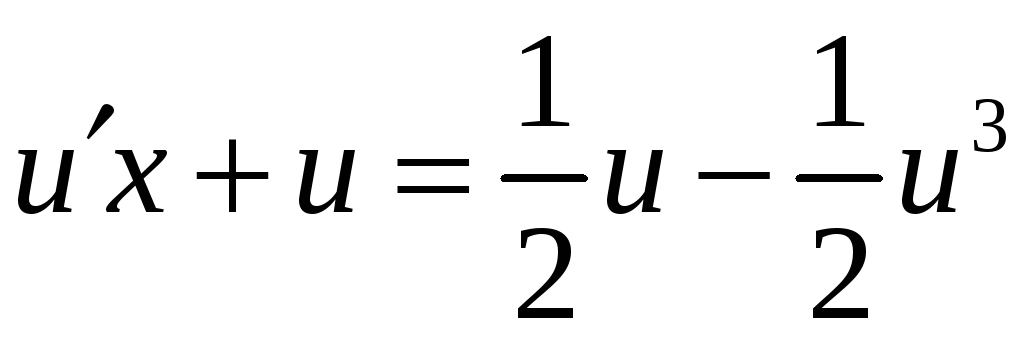 ,
,
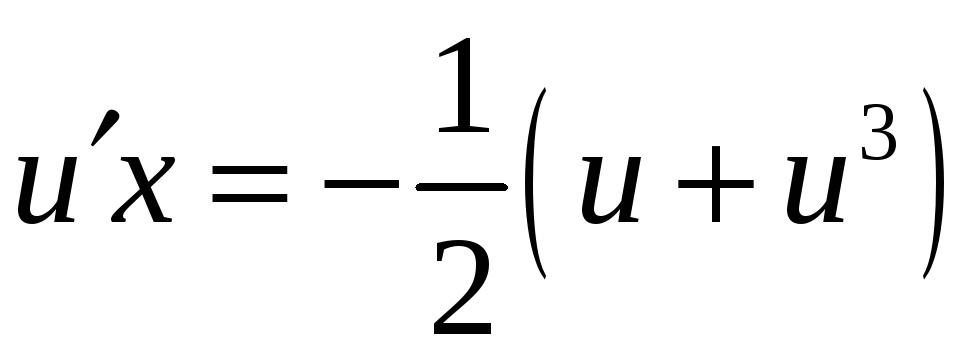 ,
,
 – получилось
уравнение
с разделяющимися переменными.
Заменим производную отношением
дифференциалов и разведём переменные
по разным частям равенства, пользуясь
свойствами пропорции
– получилось
уравнение
с разделяющимися переменными.
Заменим производную отношением
дифференциалов и разведём переменные
по разным частям равенства, пользуясь
свойствами пропорции
 .
.
Проинтегрируем обе части полученного уравнения:
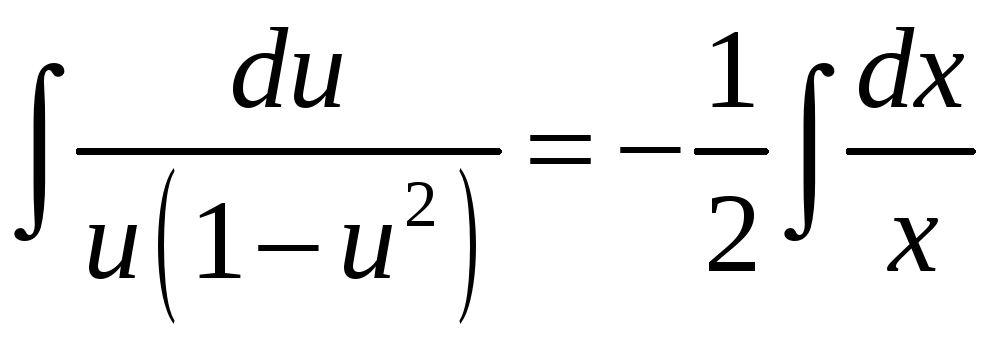 .
.
. Найдём первообразную левой части уравнения:
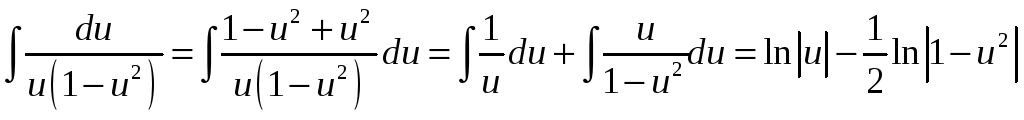 .
Тогда
.
Тогда
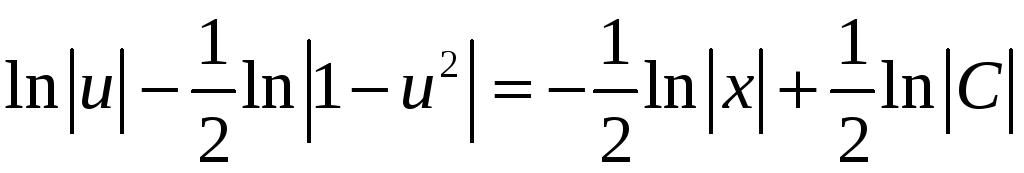 и
и
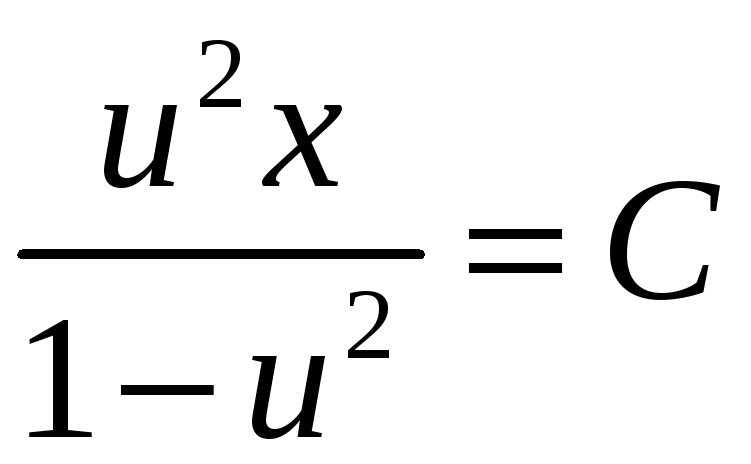 .
.
Перейдя к исходной
функции
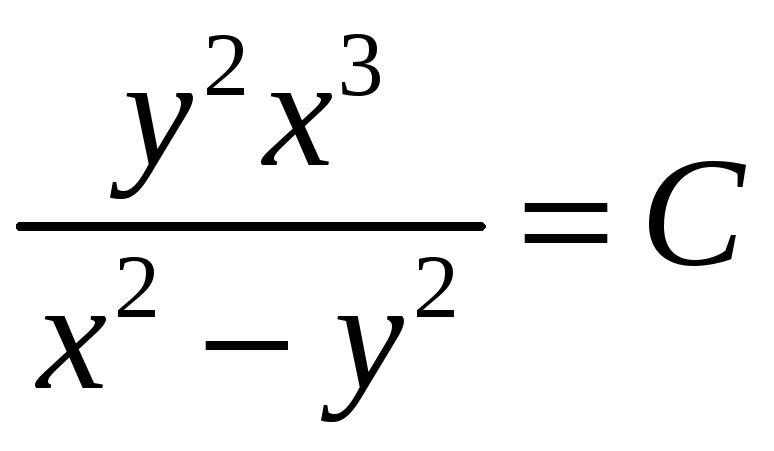 ,
получаем общий
интеграл.
,
получаем общий
интеграл.
Ответ:
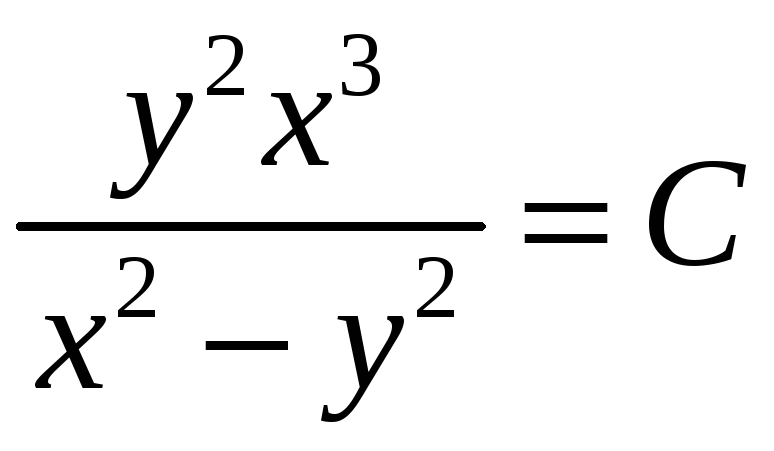 .
.
4. Решить начальную задачу Коши
![]() .
.
Решение.
Исходное уравнение
сводится к линейному
уравнению первого порядка
![]() .
Найдём сначала
общее решение этого уравнения.
.
Найдём сначала
общее решение этого уравнения.
Метод решения.
Применим метод Бернулли. Сделаем замену
![]() ,
тогда
,
тогда
![]() .
Подставим всё в
левую часть уравнение
.
Подставим всё в
левую часть уравнение
![]() .Выберем
.Выберем
![]() так, чтобы
так, чтобы
![]() .
В результате
получили два уравнения
.
В результате
получили два уравнения
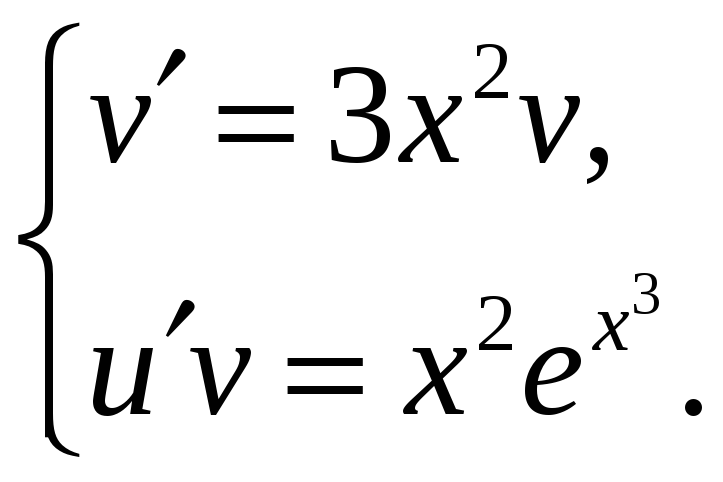
Сначала найдём
одно из решений первого уравнения
![]() ,
которое является
уравнением
с разделяющимися переменными.
Разделим переменные и проинтегрируем
обе части полученного уравнения:
,
которое является
уравнением
с разделяющимися переменными.
Разделим переменные и проинтегрируем
обе части полученного уравнения:
 ,
,
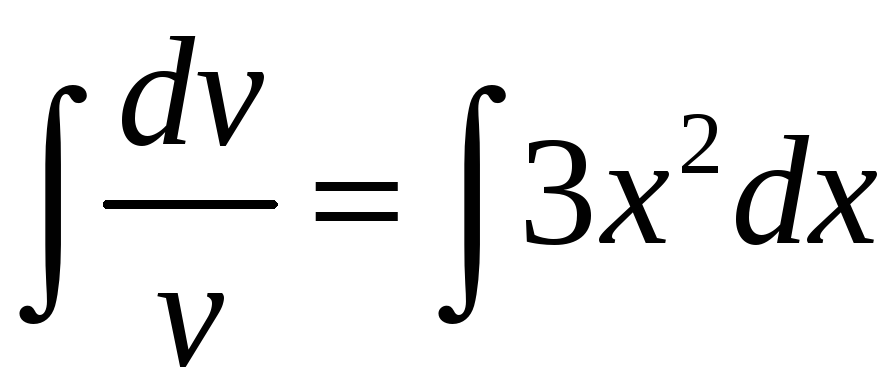 ,
,
![]() ,
,
![]() .
Подставим
.
Подставим
![]() во второе уравнение
и найдём его общее решение:
во второе уравнение
и найдём его общее решение:
![]() ,
,
![]() – уравнение с
разделяющимися переменными:
– уравнение с
разделяющимися переменными:
![]() ,
,
![]() ,
,
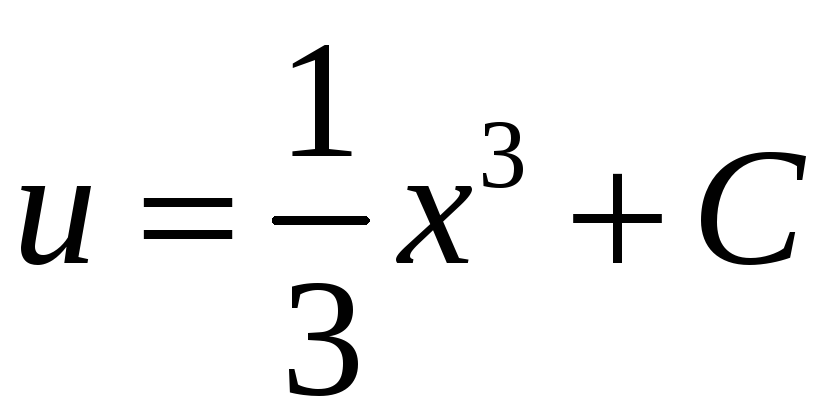 .
.
Поскольку
![]() ,
то
,
то
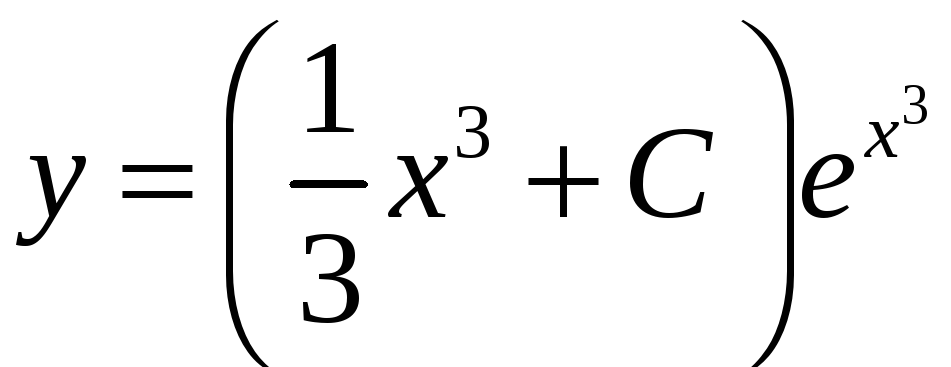 – общее решение.
– общее решение.
Подставив в это
решение начальное условие
![]() ,
получим
,
получим
![]() .
.
Частное решение
запишется
в виде
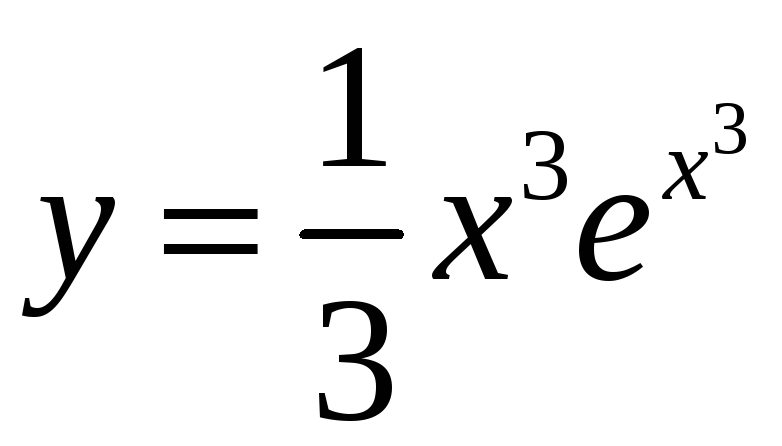 .
Ответ:
.
Ответ:
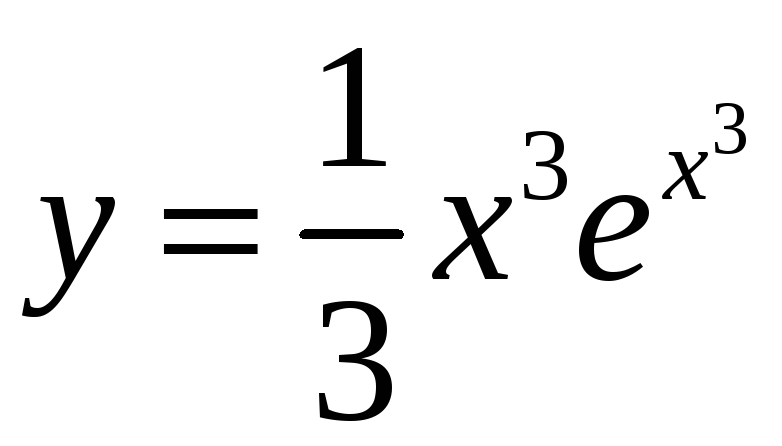 .
.
5. Найти общее решение уравнения
 .
.
Решение.
Это уравнение
сводится к уравнению
Бернулли:
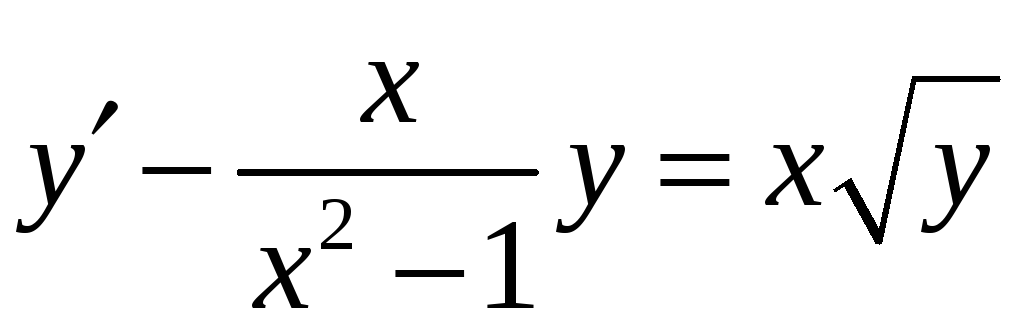 .
Применим метод
Бернулли:
.
Применим метод
Бернулли:
![]() ,
тогда
,
тогда
![]() ;
перейдём в обеих
частях уравнения к функциям u
и v:
;
перейдём в обеих
частях уравнения к функциям u
и v:
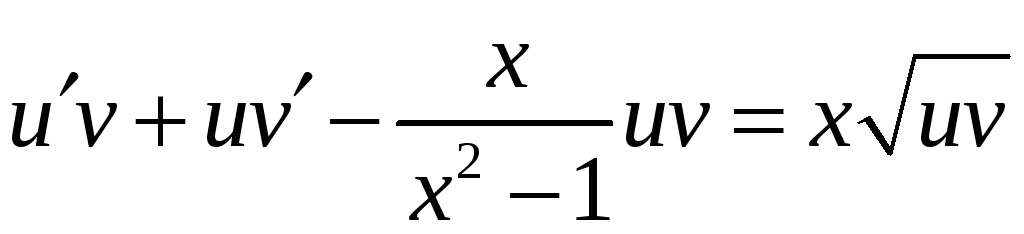 .
Выберем
.
Выберем
![]() так, чтобы
так, чтобы
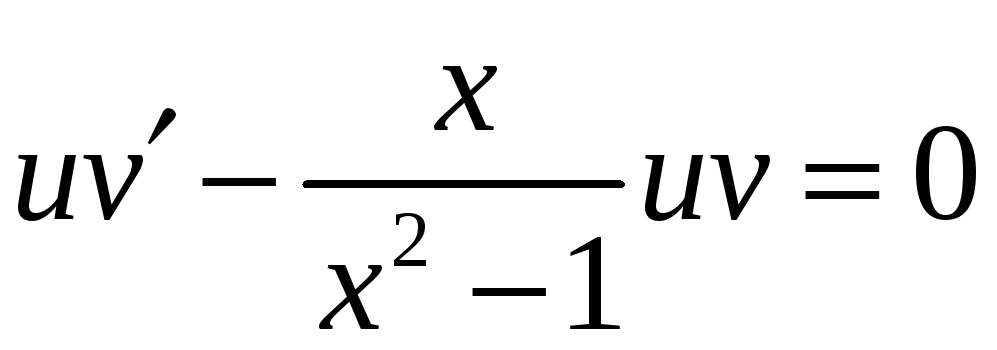 ,
после чего получим
систему двух уравнений.
,
после чего получим
систему двух уравнений.
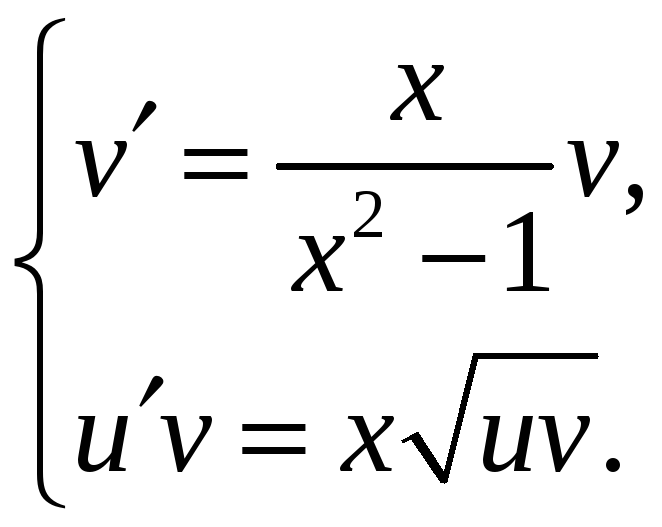 .
.
Найдём одно из
решений первого уравнения:
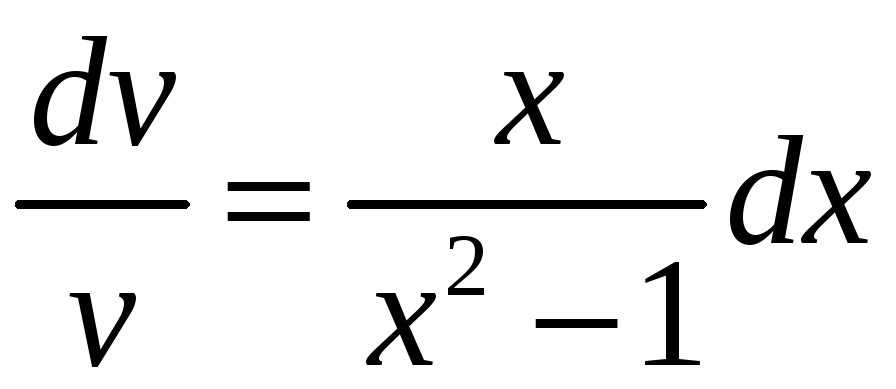 ,
,
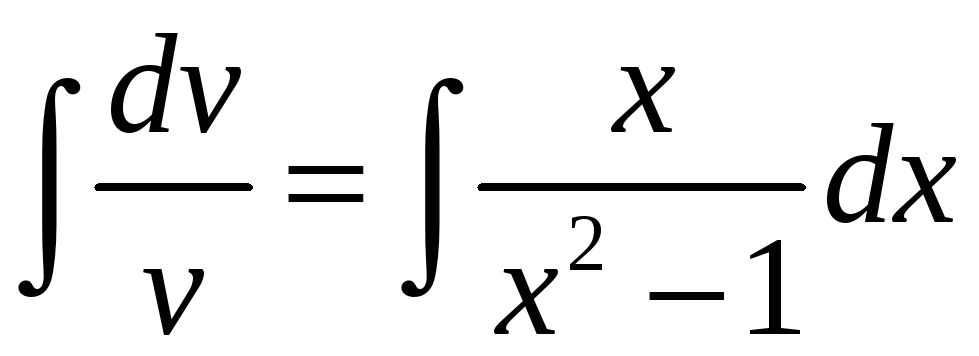 ,
,
 ,
,
![]() .
Подставим полученное
решение во второе уравнение и найдём
его общее решение:
.
Подставим полученное
решение во второе уравнение и найдём
его общее решение:
![]() ,
,
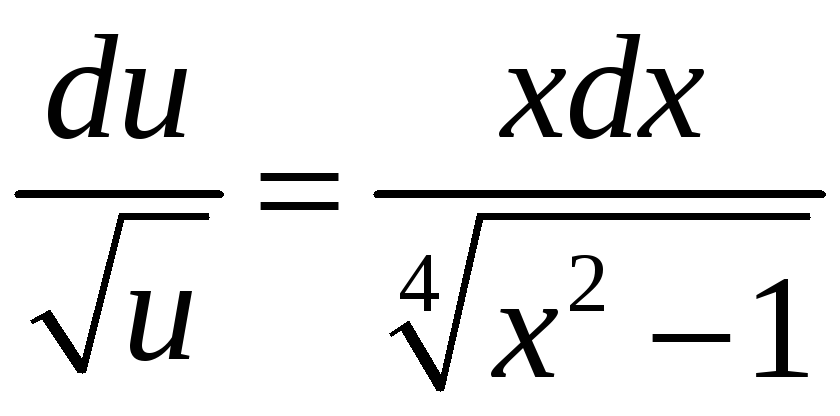 ,
,
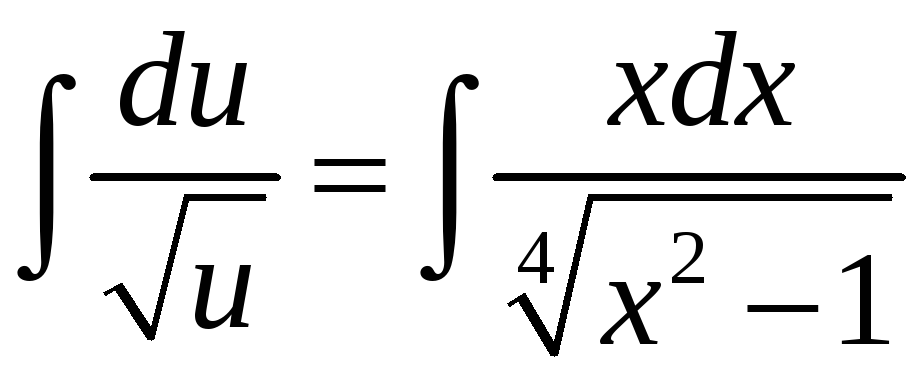 ,
,
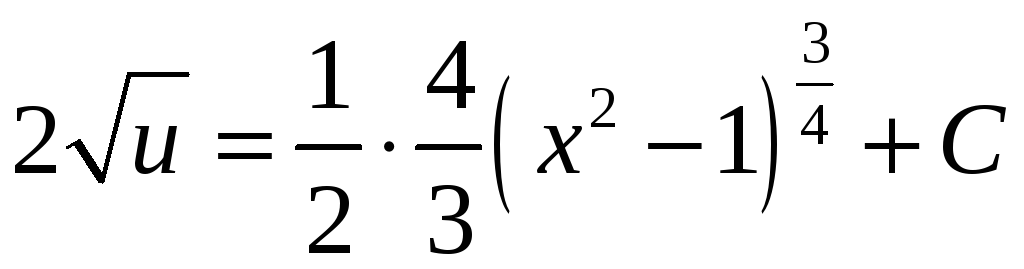 ,
,
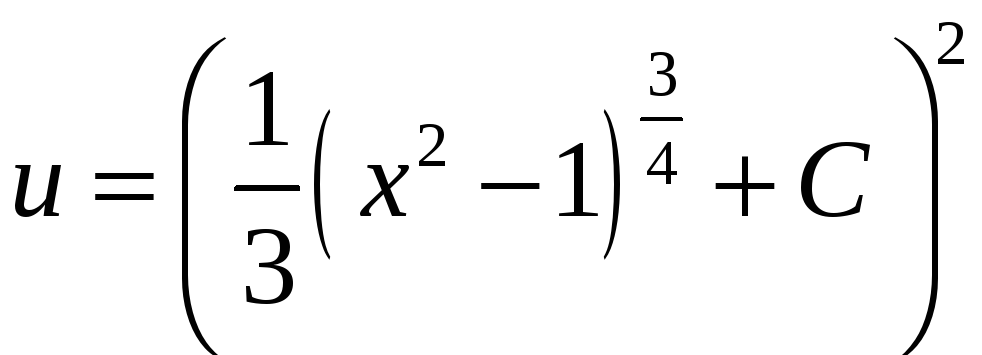 .
Общее решение
исходного уравнения запишется следующим
образом:
.
Общее решение
исходного уравнения запишется следующим
образом:
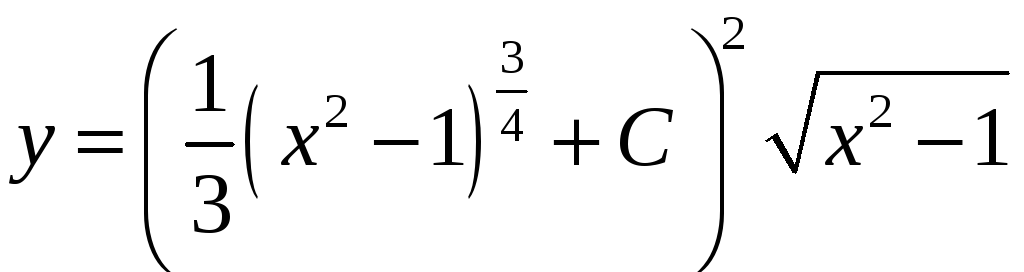 .
.
Ответ:
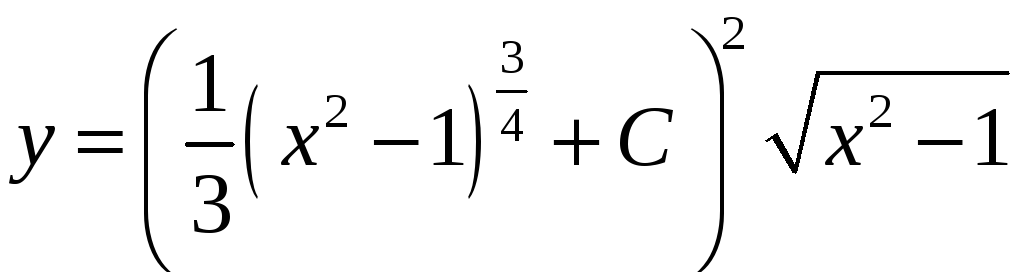 .
.
6. Решить начальную
задачу Коши:
![]() .
.
Решение.
Это уравнение
сводится к уравнению
Бернулли:
 .
Применим метод
Бернулли:
.
Применим метод
Бернулли:
![]() ,
тогда
,
тогда
![]() ;
перейдём в обеих
частях уравнения к функциям u
и v:
;
перейдём в обеих
частях уравнения к функциям u
и v:
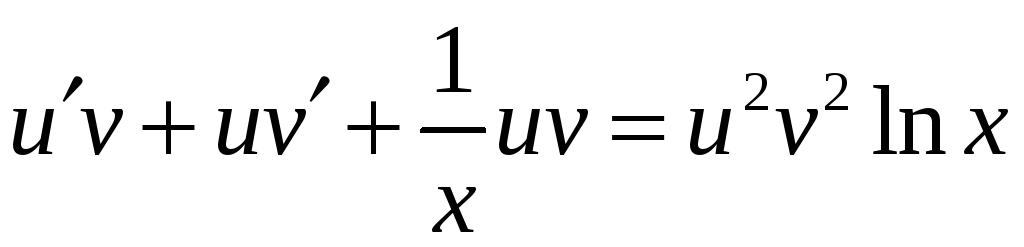 .
Выберем
.
Выберем
![]() так, чтобы
так, чтобы
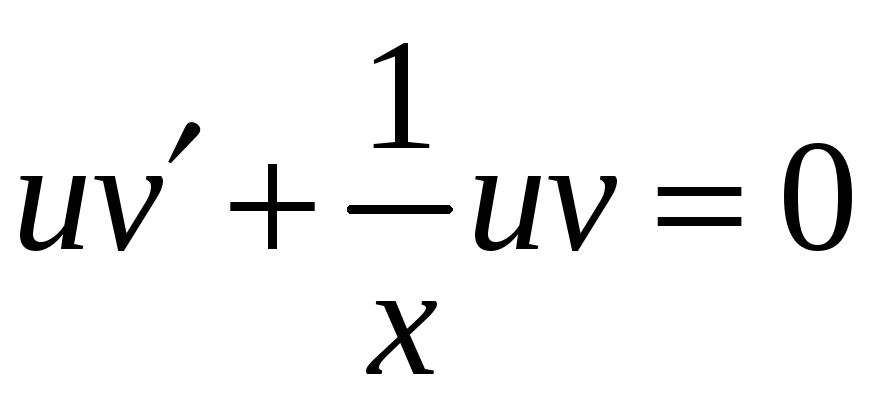 ,
после чего получим
систему двух уравнений
,
после чего получим
систему двух уравнений
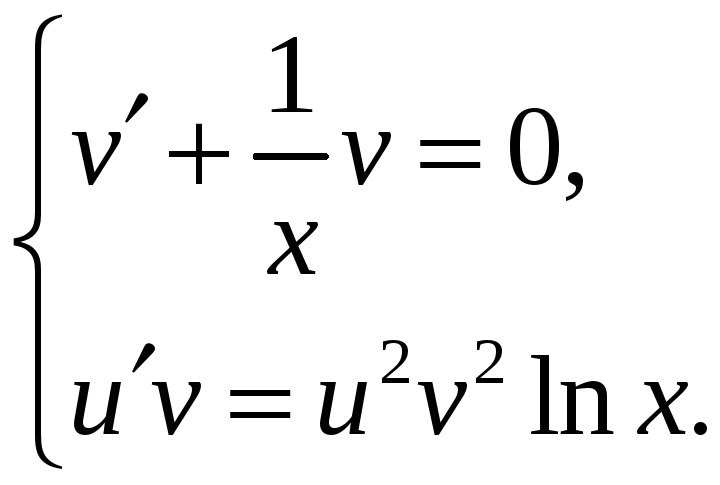
Найдём одно из
решений первого уравнения:
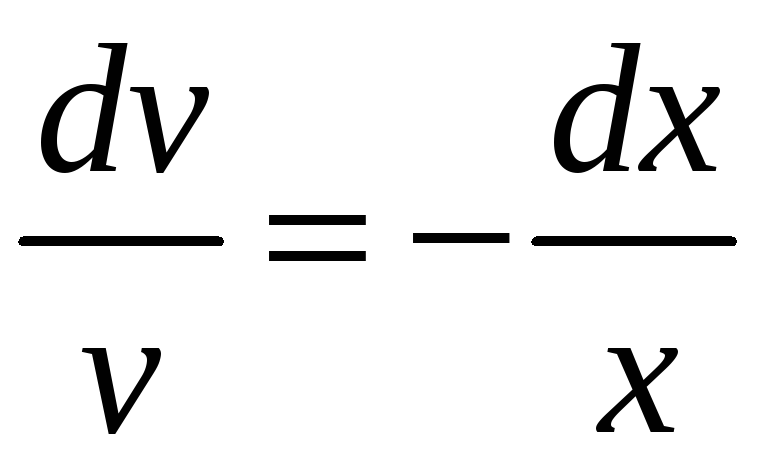 ,
,
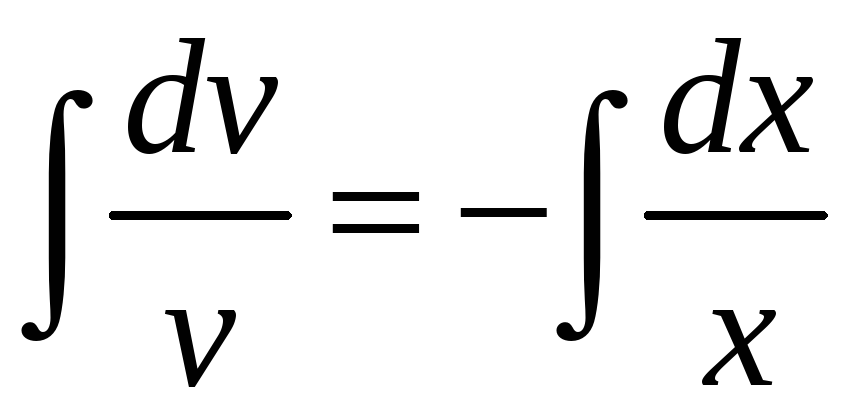 ,
,
![]() ,
,
![]() .
Подставим полученное
решение во второе уравнение и найдём
общее решение этого уравнения:
.
Подставим полученное
решение во второе уравнение и найдём
общее решение этого уравнения:
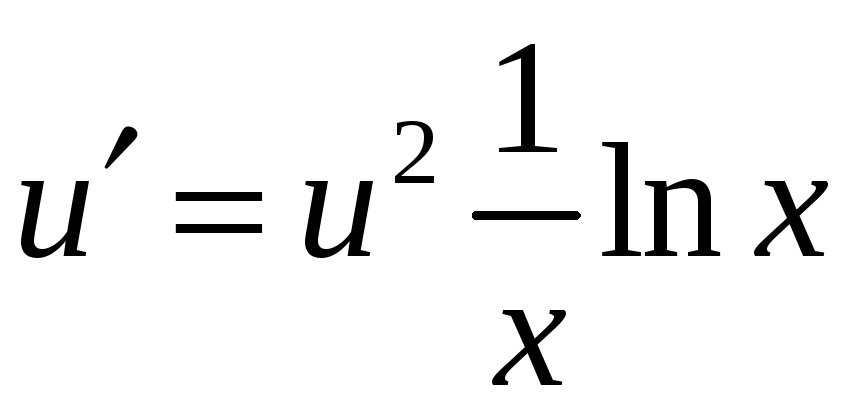 ,
,
 ,
,
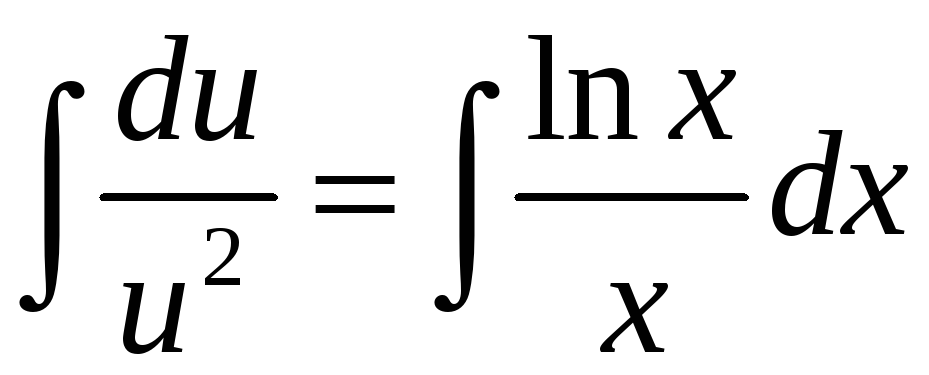 ,
,
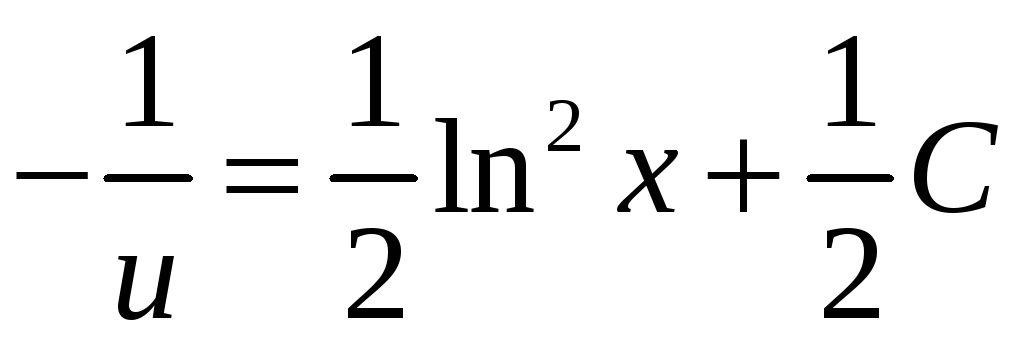 ,
,
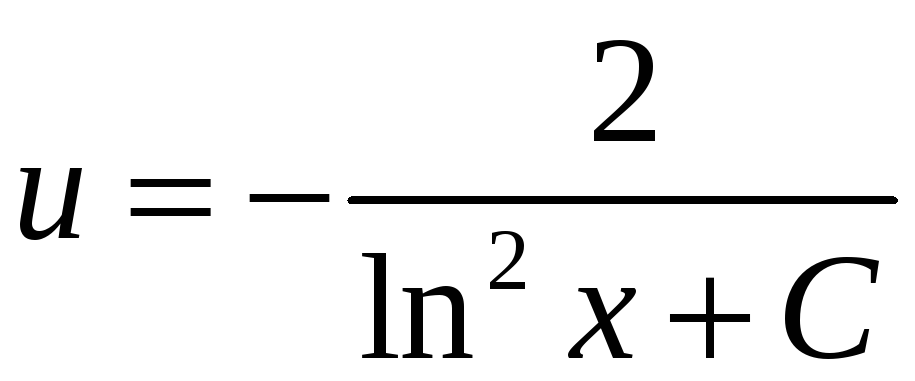 .
Общее решение
исходного уравнения запишется в виде:
.
Общее решение
исходного уравнения запишется в виде:
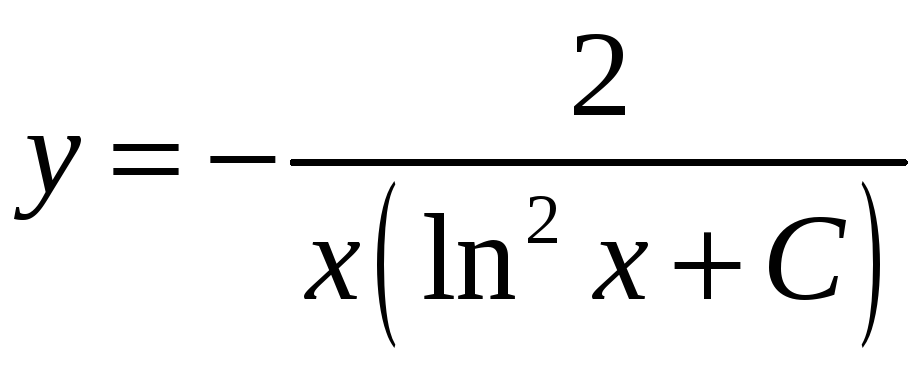 .
Подставив в это
решение начальное условие
.
Подставив в это
решение начальное условие
![]() ,
получим, что
,
получим, что
![]() ,
и решение задачи Коши окончательно
принимает вид
,
и решение задачи Коши окончательно
принимает вид
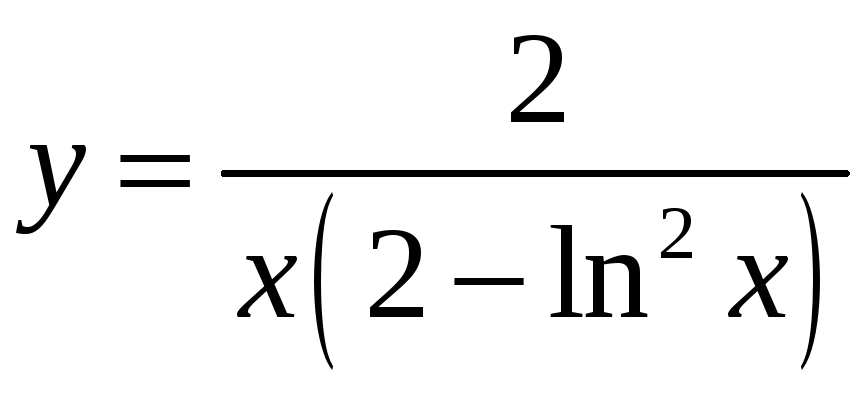 .
Ответ:
.
Ответ:
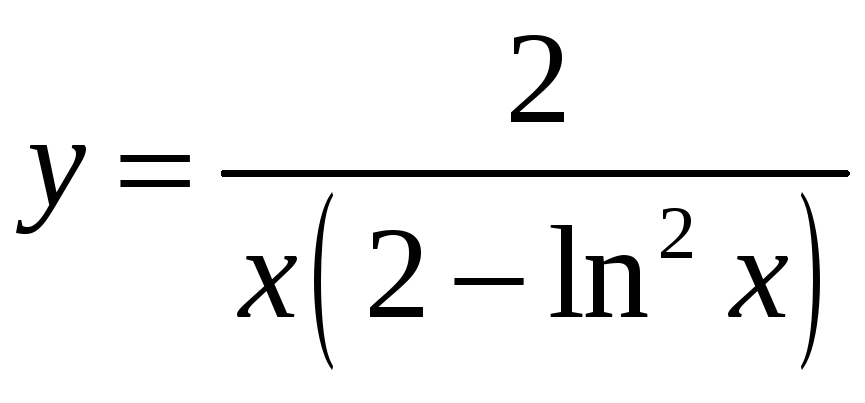 .
.
7. Найти общий интеграл уравнения
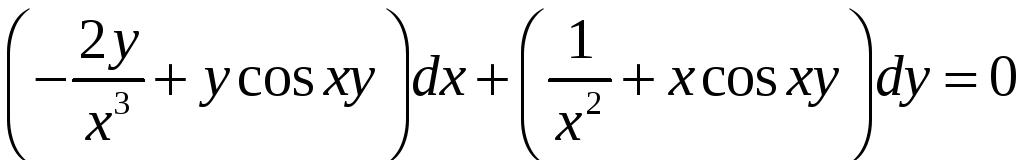 .
.
Решение.
Покажем, что это уравнение является
уравнением
в полных дифференциалах.
Пусть
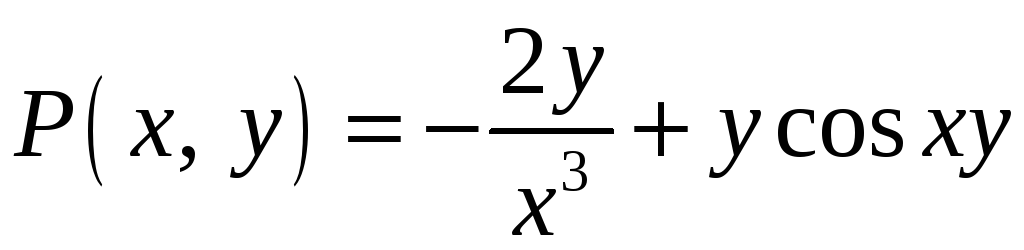 и
и
 .
Проверим равенство
.
Проверим равенство
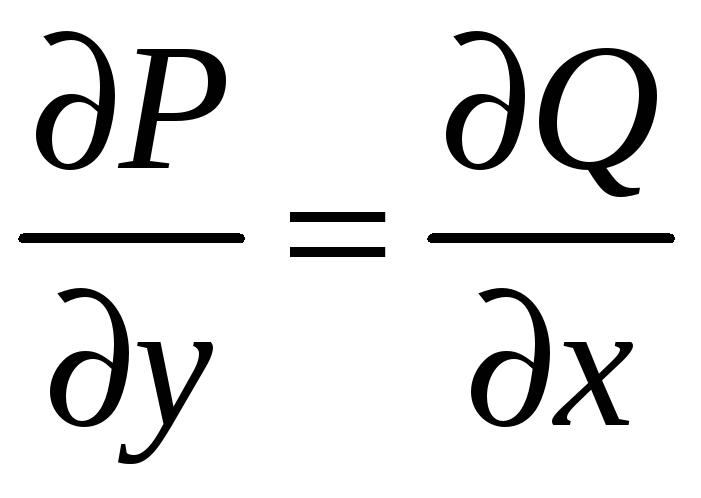 ,
которое является
условием того, что уравнение
,
которое является
условием того, что уравнение
![]() есть
уравнение в полных дифференциалах.
Поскольку
есть
уравнение в полных дифференциалах.
Поскольку
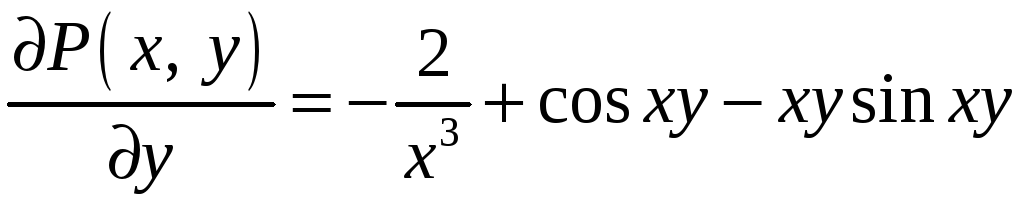 ,
,
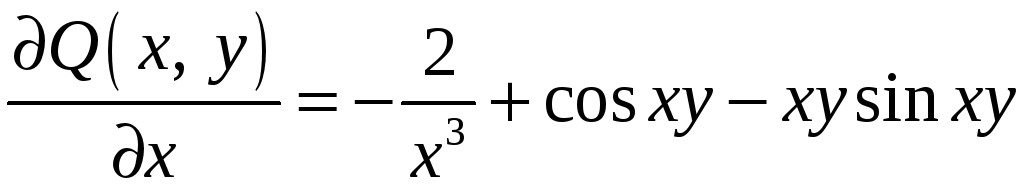 ,
то
,
то
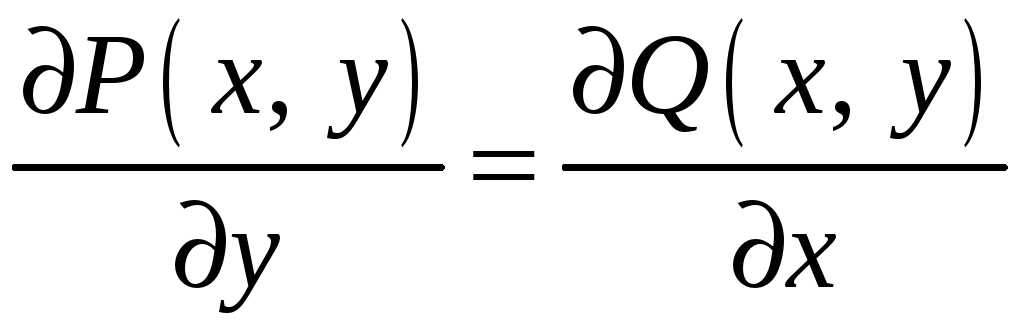 ,
следовательно, исходное уравнение
действительно является уравнением в
полных дифференциалах, т.е. существует
функция
,
следовательно, исходное уравнение
действительно является уравнением в
полных дифференциалах, т.е. существует
функция
![]() ,
для которой
,
для которой
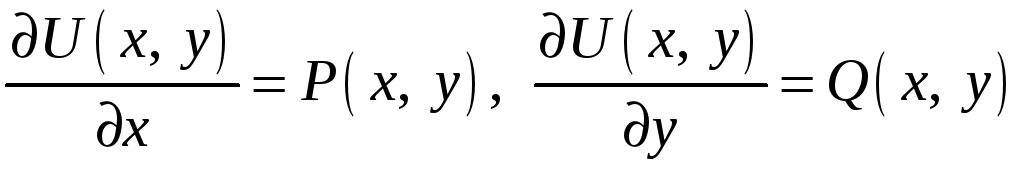 ,
,
и дифференциальное
уравнение
![]() сводится к уравнению
сводится к уравнению
![]() .
Найдём функцию
.
Найдём функцию
![]() .
.
Поскольку для исходного уравнения
 и
и
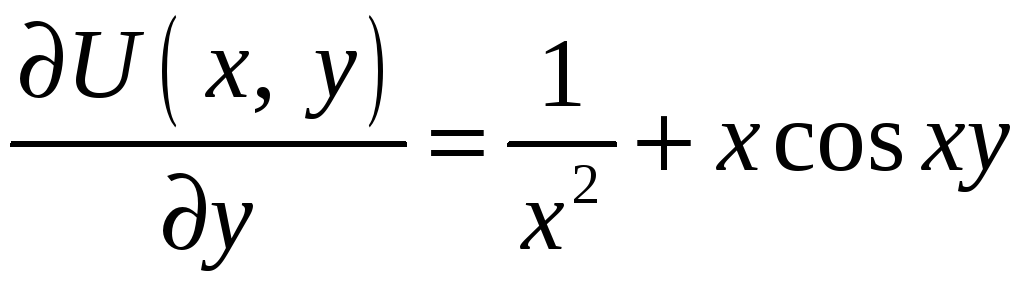 ,
,
то
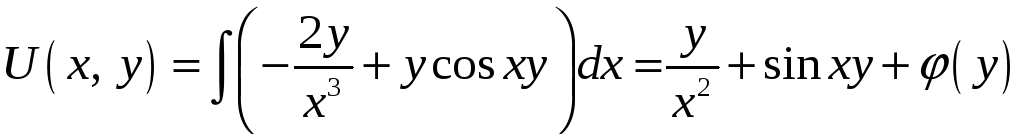 .
От этой функции
найдём частную производную по переменной
y:
.
От этой функции
найдём частную производную по переменной
y:
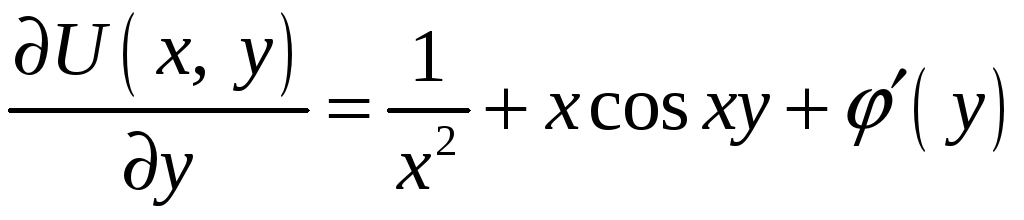 .
Сравнивая это
выражение со второй частной производной
.
Сравнивая это
выражение со второй частной производной
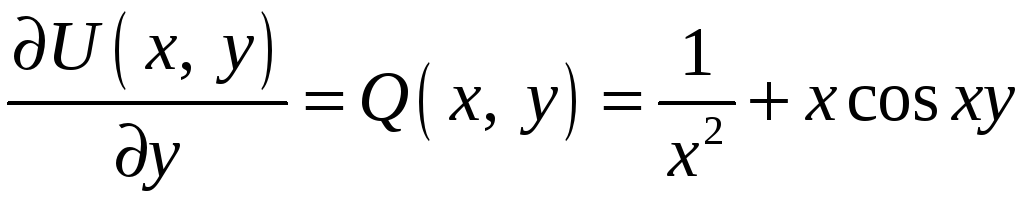 ,
получим, что
,
получим, что
![]() .
Следовательно,
.
Следовательно,
![]() const
const![]() .
Итак, с точностью
до постоянной нашли функцию
.
Итак, с точностью
до постоянной нашли функцию
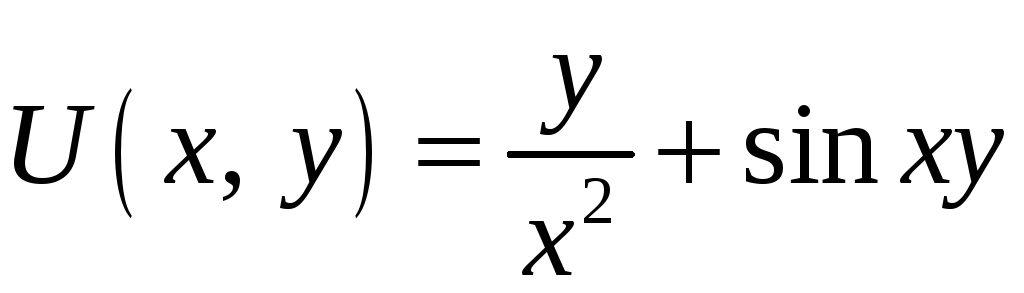 ,
но
,
но
![]() ,
тогда
,
тогда
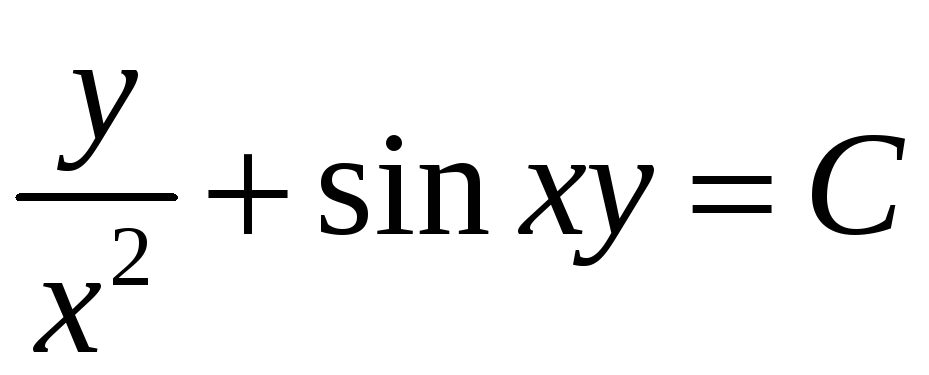 .
Это
равенство и
определяет общий интеграл данного
дифференциального уравнения.
.
Это
равенство и
определяет общий интеграл данного
дифференциального уравнения.
Ответ:
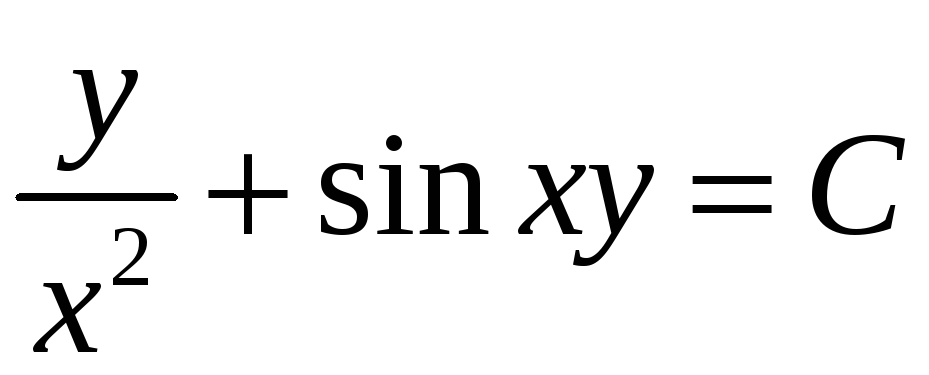 .
.
II. В следующих трёх примерах даны дифференциальные уравнения второго порядка, которые допускают понижение порядка.
8. Найти частное решение дифференциального уравнения
![]() при начальных
условиях
при начальных
условиях
![]() .
.
и вычислить
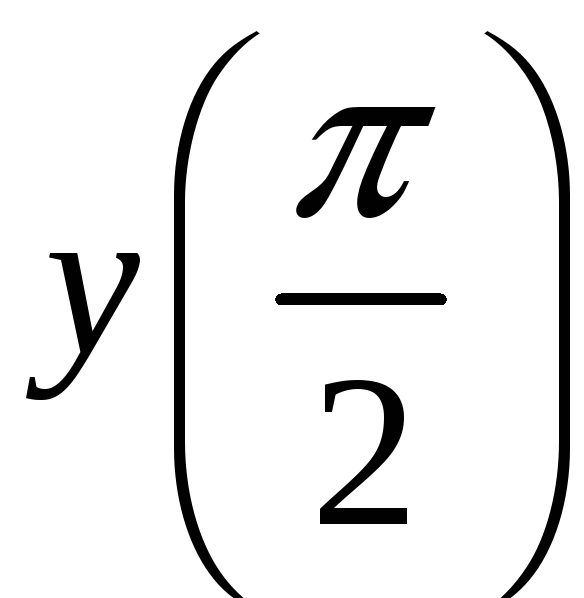 с точностью до
двух знаков после запятой.
с точностью до
двух знаков после запятой.
Решение.
Дано дифференциальное уравнение второго
порядка. Чтобы найти его частное решение,
сначала найдём общее решение этого
уравнения. Для этого понизим порядок
дифференциального уравнения. Пусть
![]() ,
тогда
,
тогда
![]() и
и
![]() .
.
Получили уравнение с разделяющимися переменными первого порядка. Найдём общее решение этого уравнения. Поскольку
![]()
![]() ,
то
,
то
![]() .
Так как
.
Так как
![]() ,
то
,
то
![]()
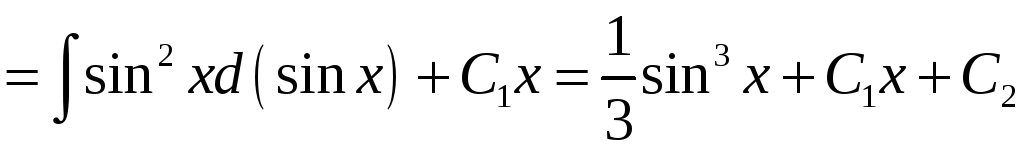 .
Итак,
.
Итак,
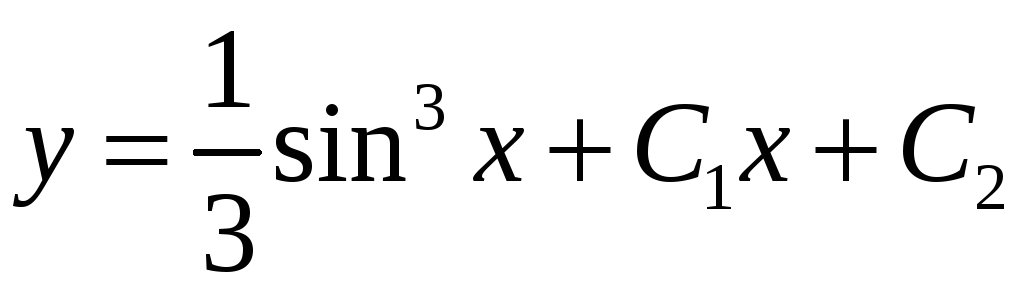 –
общее решение
исходного уравнения. Реализуя начальные
условия, получим
–
общее решение
исходного уравнения. Реализуя начальные
условия, получим
![]() и
и
![]() ;
тогда
получается
частное решение
;
тогда
получается
частное решение
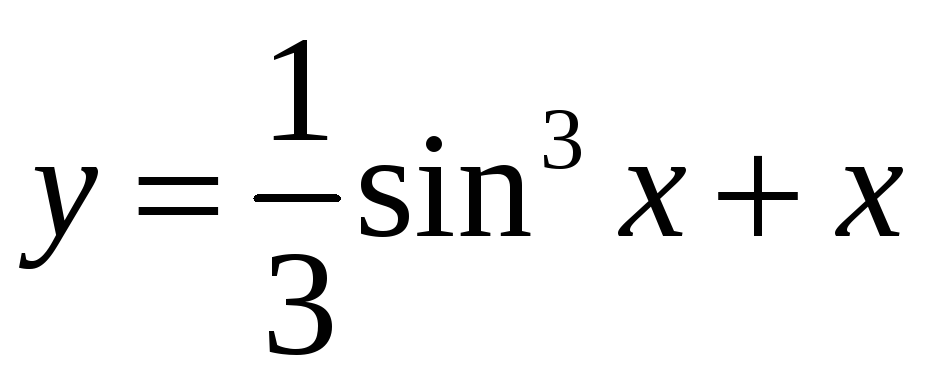 .
.
Теперь можно
вычислить:
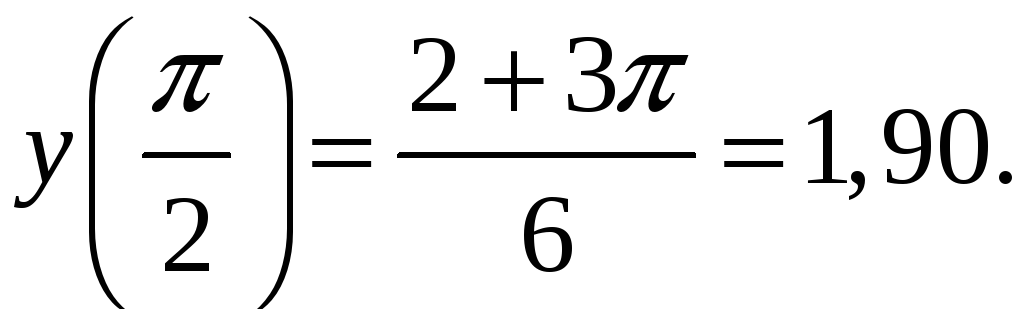
Ответ:
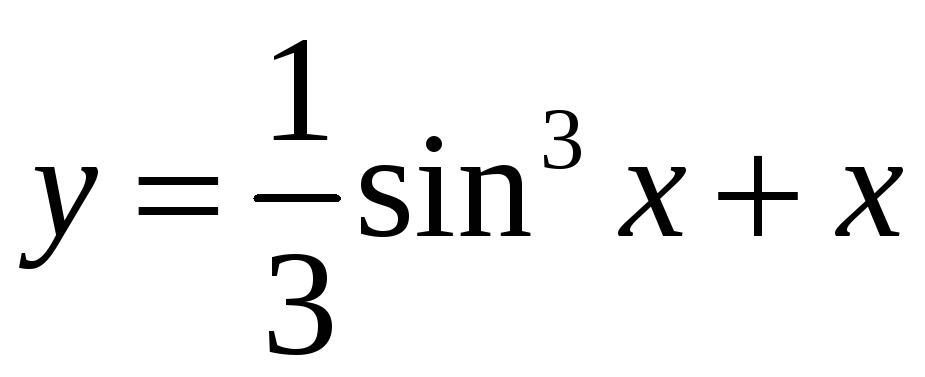 ,
,
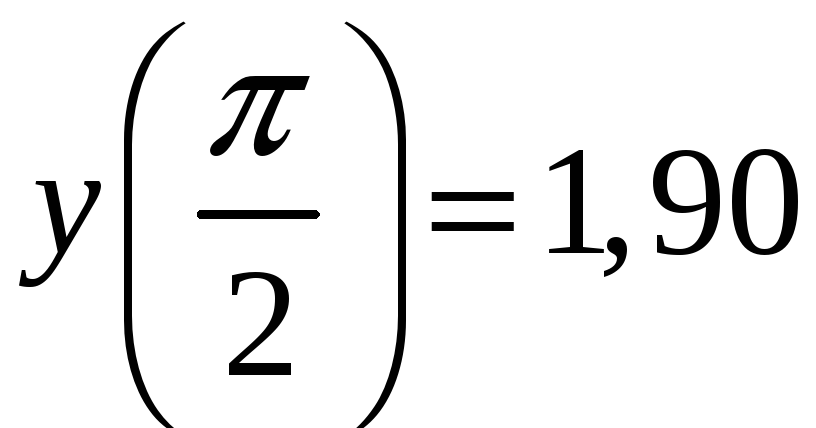 .
.
9. Найти общее решение уравнения
![]() .
.
Решение.
Поскольку в уравнении явно отсутствует
функция у,
понизим порядок уравнения, сделав замену
![]() .
Тогда
.
Тогда
![]() и дифференциальное уравнение примет
вид
и дифференциальное уравнение примет
вид
![]() ,
,
 – уравнение с
разделяющимися переменными.
Разделим переменные и проинтегрируем
полученное уравнение:
– уравнение с
разделяющимися переменными.
Разделим переменные и проинтегрируем
полученное уравнение:
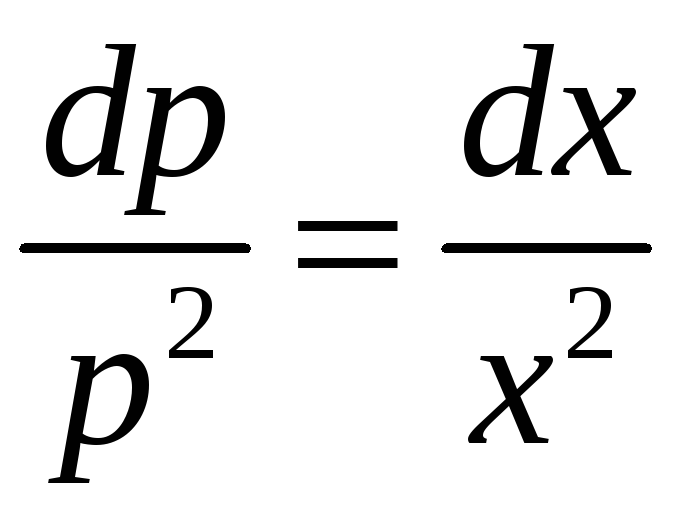 ,
,
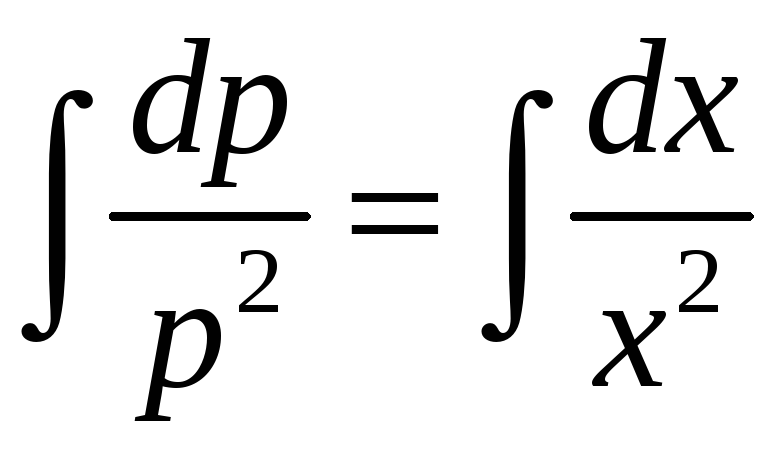 ,
,
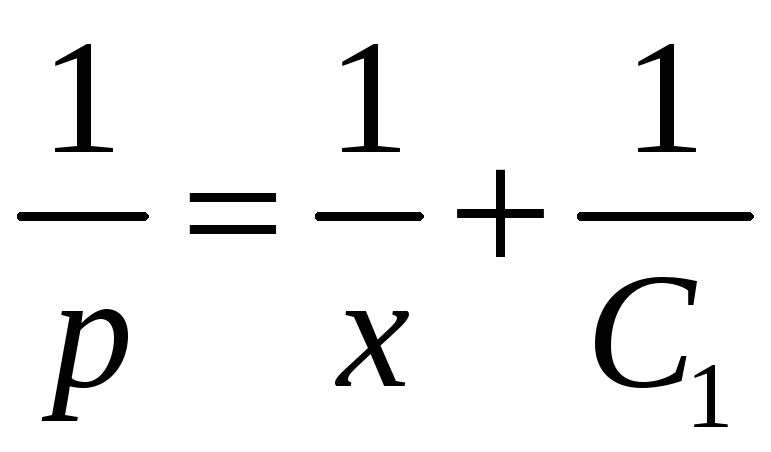 ,
,
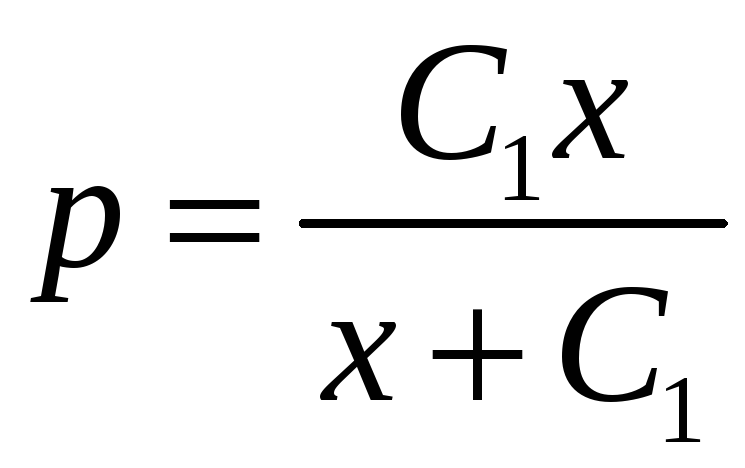 .
Учитывая, что
.
Учитывая, что
![]() ,
получаем уравнение
с разделяющимися переменными
–
,
получаем уравнение
с разделяющимися переменными
–
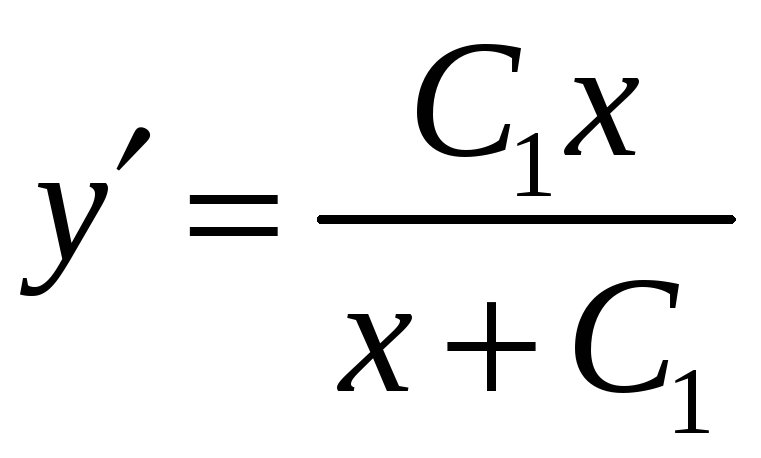 .
Интегрируем его:
.
Интегрируем его:
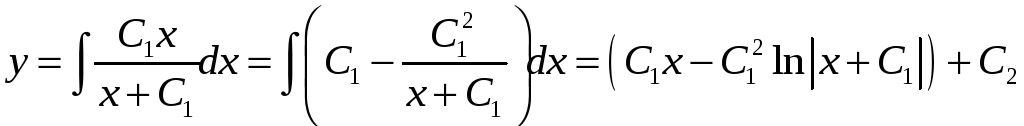 .
.
Итак,
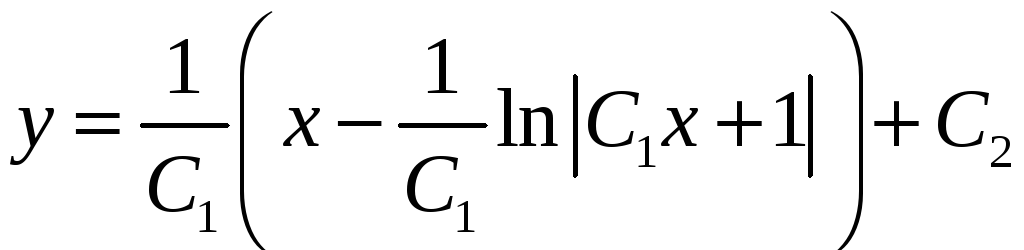 – общее решение
исходного уравнения.
Ответ:
– общее решение
исходного уравнения.
Ответ:
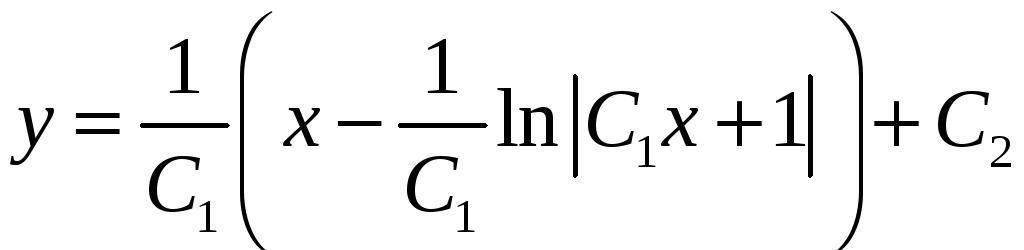 .
.
10. Решить задачу Коши для дифференциального уравнения второго порядка
![]() .
.
Решение.
Поскольку в этом уравнении явно
отсутствует переменная х,
то для понижения его порядка сделаем
замену
![]() .
Тогда
.
Тогда
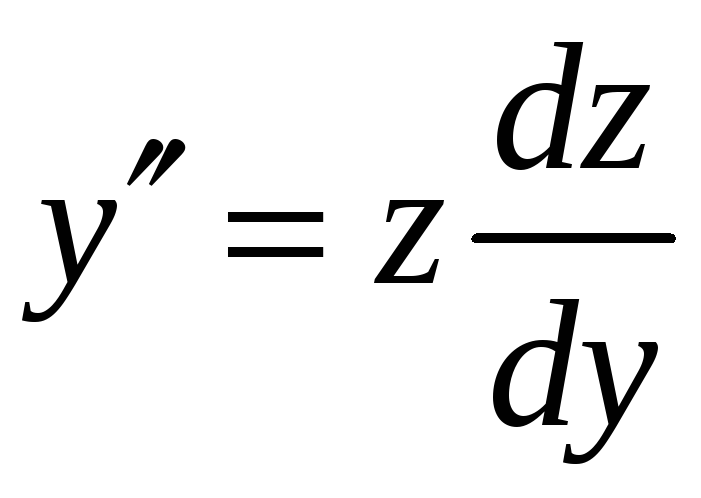 и исходное уравнение примет вид
и исходное уравнение примет вид
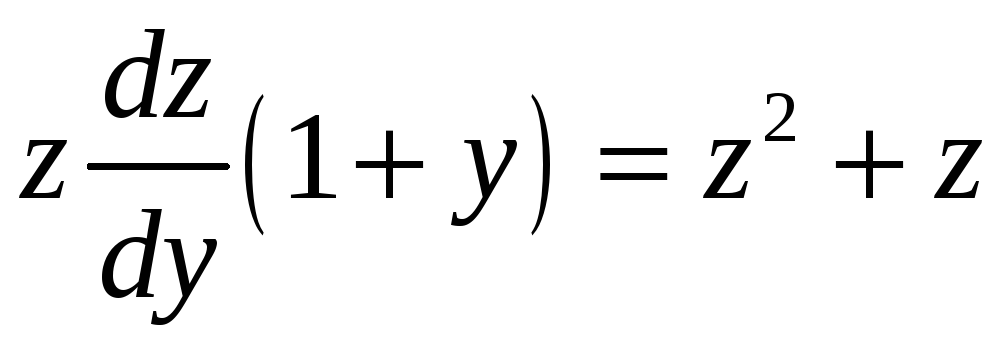 или
или
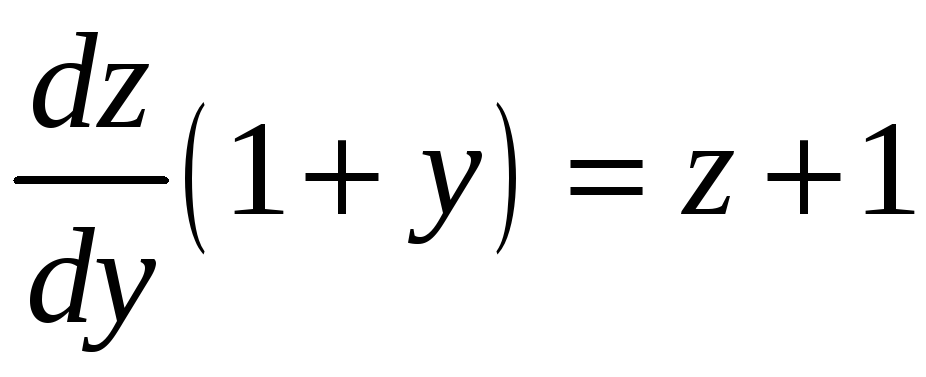 ,
откуда
,
откуда
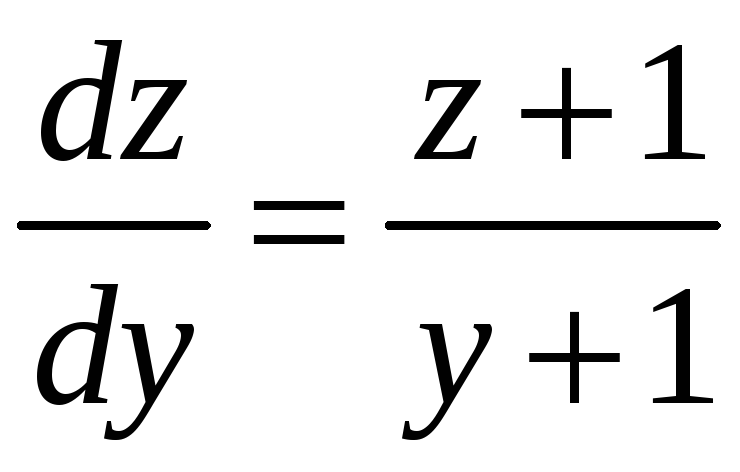 – уравнение с
разделяющимися переменными.
Разделив переменные, проинтегрируем
полученное уравнение:
– уравнение с
разделяющимися переменными.
Разделив переменные, проинтегрируем
полученное уравнение:
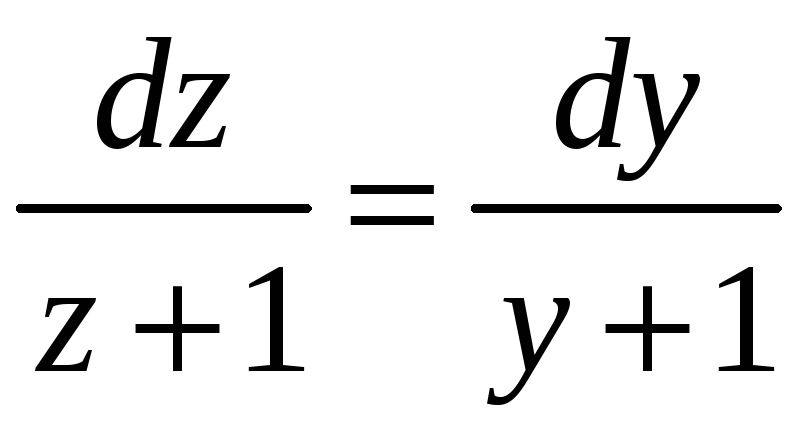 ,
,
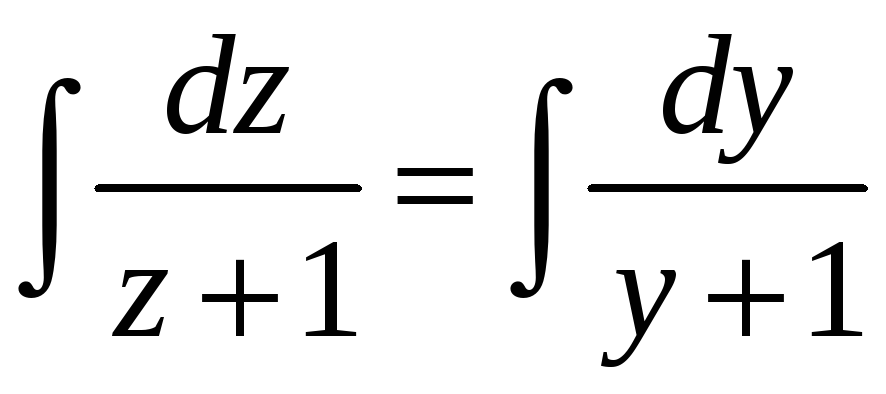 ,
,
![]() ,
,
![]() или
или
![]() .
При нахождении частного решения значения
произвольных постоянных
.
При нахождении частного решения значения
произвольных постоянных
![]() и
и
![]() можно находить по
мере их появления. Сейчас можно найти
значение постоянной
можно находить по
мере их появления. Сейчас можно найти
значение постоянной
![]() ,
подставив в
последнее равенство начальные условия
,
подставив в
последнее равенство начальные условия
![]() :
:
![]() .
Тогда
.
Тогда
![]() – уравнение с
разделяющимися переменными.
Разделив переменные, проинтегрируем
полученное уравнение:
– уравнение с
разделяющимися переменными.
Разделив переменные, проинтегрируем
полученное уравнение:
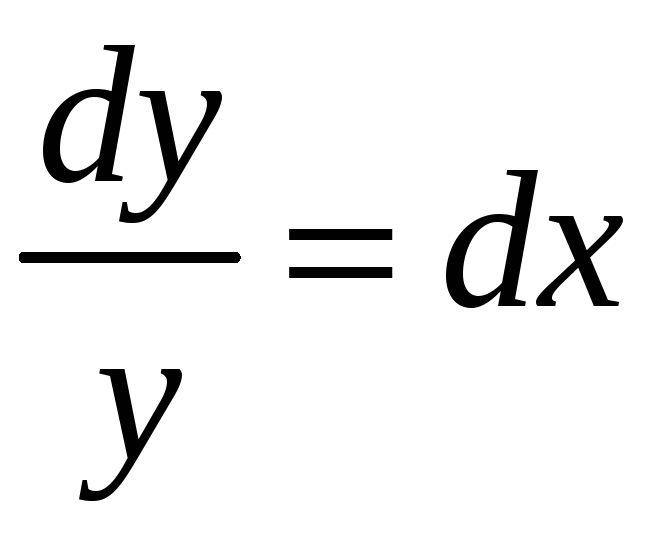 ,
,
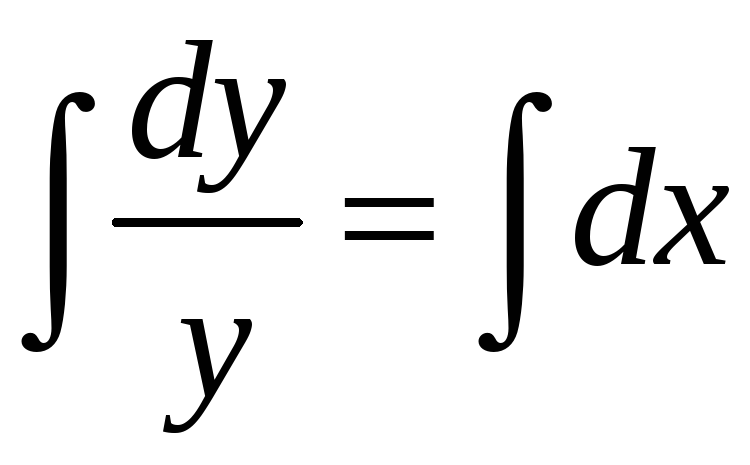 ,
,
![]() .
Теперь найдём
значение постоянной
.
Теперь найдём
значение постоянной
![]()
![]() .
Итак,
.
Итак,
![]() –
частное решение
исходного уравнения.
–
частное решение
исходного уравнения.
