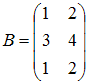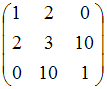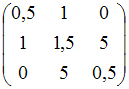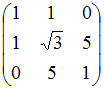- •2. Одна из вершин треугольника находится в полюсе , две другие имеют координаты и . Тогда площадь треугольника равна …
- •Площадь треугольника можно вычислить по формуле , где – угол между сторонами и . Тогда .
- •Тема: Прямая на плоскости
- •Тема: Плоскость в пространстве
- •Тема: Кривые второго порядка
- •Тема: Определение линейного пространства
Тема: Кривые второго порядка
1. Асимптоты
гиперболы
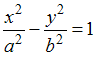 задаются
уравнениями вида
задаются
уравнениями вида
![]() .
.
Фокусы гиперболы,
заданной каноническим уравнением
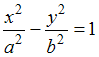 ,
имеют координаты
,
имеют координаты
![]() и
и
![]() ,
где
,
где
![]() ,
а эксцентриситет
,
а эксцентриситет
![]() .
.
2.
Каноническое уравнение эллипса имеет
вид
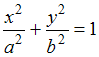 ;
фокусы эллипса имеют координаты
;
фокусы эллипса имеют координаты
![]() и
и
![]() ,
где
,
где
![]() ,
а эксцентриситет
,
а эксцентриситет
![]() .
Тема: Кривые
второго порядка
Радиус
окружности
.
Тема: Кривые
второго порядка
Радиус
окружности
![]() равен …
равен …
|
|
|
|
2 |
Пример.
Мнимая полуось гиперболы
![]() равна …
равна …
Выделим в уравнении
![]() полный
квадрат по переменной
полный
квадрат по переменной
![]() :
:
![]() ,
или
,
или
![]() .
Разделив обе части этого уравнение на
36, получим уравнение гиперболы в виде
.
Разделив обе части этого уравнение на
36, получим уравнение гиперболы в виде
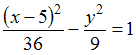 .
Отсюда мнимая полуось
.
Отсюда мнимая полуось
![]() .
.
Тема: Кривые
второго порядка
Фокусы
эллипса имеют координаты
![]() и
и
![]() ,
а его эксцентриситет равен 0,6. Тогда
каноническое уравнение эллипса имеет
вид …
,
а его эксцентриситет равен 0,6. Тогда
каноническое уравнение эллипса имеет
вид …
Решение:
Каноническое
уравнение эллипса имеет вид
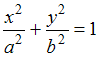 ;
фокусы эллипса имеют координаты
;
фокусы эллипса имеют координаты
![]() и
и
![]() ,
где
,
где
![]() ,
а эксцентриситет
,
а эксцентриситет
![]() .
Тогда
.
Тогда
![]() ,
,
![]() ,
,
![]() .
Следовательно, получаем уравнение
.
Следовательно, получаем уравнение
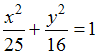 .
.
Тема:
Кривые второго порядка
Соотношение
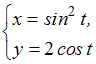 в
прямоугольной декартовой системе
координат задает …
в
прямоугольной декартовой системе
координат задает …
|
|
|
|
параболу |
|
|
|
|
гиперболу |
|
|
|
|
эллипс |
|
|
|
|
окружность |
Решение:
Вычислим
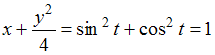 ,
то есть
,
то есть
![]() .
Тогда в прямоугольной декартовой
системе координат данное уравнение
задает параболу с вершиной в точке
.
Тогда в прямоугольной декартовой
системе координат данное уравнение
задает параболу с вершиной в точке
![]()
Тема:
Кривые второго порядка
Расстояние
между фокусами гиперболы
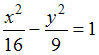 равно
…
равно
…
|
|
|
|
10 |
|
|
|
|
7 |
|
|
|
|
5 |
|
|
|
|
2,5 |
Решение:
Фокусы
гиперболы, заданной каноническим
уравнением
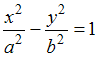 ,
имеют координаты
,
имеют координаты
![]() и
и
![]() ,
где
,
где
![]() .
Тогда
.
Тогда
![]() .
То есть расстояние между двумя точками
.
То есть расстояние между двумя точками
![]() и
и
![]() равно
10.
равно
10.
Тема: Определение линейного пространства
На
линейном пространстве
![]() задана
операция …
задана
операция …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Множество
![]() образует
линейное пространство, если для любых
2-х его элементов
образует
линейное пространство, если для любых
2-х его элементов
![]() определены
операции сложения
определены
операции сложения
![]() и
умножения на действительное число
и
умножения на действительное число
![]() ;
;
![]() со
свойствами:
1.
со
свойствами:
1.
![]() 2.
2.
![]() 3.
3.
![]() 4.
4.
![]() 5.
5.
![]() 6.
6.
![]()
Тема: Определение линейного пространства Среди представленных множеств линейное пространство образует …
|
|
|
|
множество
всех векторов, принадлежащих пространству
|
|
|
|
|
множество
всех векторов пространства
|
|
|
|
|
множество натуральных чисел |
|
|
|
|
множество всех отрицательных вещественных чисел |
Решение:
Множество
![]() образует
линейное пространство, если для любых
двух его элементов
образует
линейное пространство, если для любых
двух его элементов
![]() определены
операции сложения
определены
операции сложения
![]() и
умножения на действительное число
и
умножения на действительное число
![]() ;
;
![]() со
свойствами:
1.
со
свойствами:
1.
![]() 2.
2.
![]() 3.
3.
![]() 4.
4.
![]() 5.
5.
![]() 6.
6.
![]() При
проверке аксиом получим: векторы
пространства
При
проверке аксиом получим: векторы
пространства
![]() ,
образующие острый угол с положительным
направлением оси ординат, не образуют
линейного пространства, т.к. умножение
на отрицательное число делает этот угол
тупым; для множество натуральных чисел
и множество всех отрицательных
вещественных чисел не выполняется
шестая аксиома.
,
образующие острый угол с положительным
направлением оси ординат, не образуют
линейного пространства, т.к. умножение
на отрицательное число делает этот угол
тупым; для множество натуральных чисел
и множество всех отрицательных
вещественных чисел не выполняется
шестая аксиома.
Тема:
Определение линейного пространства
На
линейном пространстве
![]() задана
операция …
задана
операция …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Множество
![]() образует
линейное пространство, если для любых
2-х его элементов
образует
линейное пространство, если для любых
2-х его элементов
![]() определены
операции сложения
определены
операции сложения
![]() и
умножения на действительное число
и
умножения на действительное число
![]() ;
;
![]() со
свойствами:
1.
со
свойствами:
1.
![]() 2.
2.
![]() 3.
3.
![]() 4.
4.
![]() 5.
5.
![]() 6.
6.
![]() Тема:
Определение линейного пространства
Пример.
Среди
представленных множеств линейное
пространство образует …
Тема:
Определение линейного пространства
Пример.
Среди
представленных множеств линейное
пространство образует …
|
|
|
|
множество всех комплексных чисел |
|
|
|
|
множество всех натуральных чисел |
|
|
|
|
множество всех положительных иррациональных чисел |
|
|
|
|
множество всех отрицательных рациональных чисел |
Решение:
Множество
![]() образует
линейное пространство, если для любых
2-х его элементов
образует
линейное пространство, если для любых
2-х его элементов
![]() определены
операции сложения
определены
операции сложения
![]() и
умножения на действительное число
и
умножения на действительное число
![]() ;
;
![]() со
свойствами:
1.
со
свойствами:
1.
![]() 2.
2.
![]() 3.
3.
![]() 4.
4.
![]() 5.
5.
![]() 6.
6.
![]() При
проверке аксиом получим: для множества
натуральных чисел, множества всех
положительных иррациональных чисел и
множества всех отрицательных рациональных
чисел не выполняется шестая аксиома.
При
проверке аксиом получим: для множества
натуральных чисел, множества всех
положительных иррациональных чисел и
множества всех отрицательных рациональных
чисел не выполняется шестая аксиома.
Тема:
Определение линейного пространства
Аксиомой
линейного пространства
![]() является
…
является
…
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Множество
![]() образует
линейное пространство, если для любых
двух его элементов
образует
линейное пространство, если для любых
двух его элементов
![]() определены
операции сложения
определены
операции сложения
![]() и
умножения на действительное число
и
умножения на действительное число
![]() ;
;
![]() со
свойствами:
1.
со
свойствами:
1.
![]() 2.
2.
![]() 3.
3.
![]() 4.
4.
![]() 5.
5.
![]() 6.
6.
![]()
Тема: Определение линейного пространства Среди представленных множеств линейное пространство образует …
|
|
|
|
множество всех комплексных чисел |
|
|
|
|
множество всех натуральных чисел |
|
|
|
|
множество всех положительных иррациональных чисел |
|
|
|
|
множество всех отрицательных рациональных чисел |
Решение:
Множество
![]() образует
линейное пространство, если для любых
2-х его элементов
образует
линейное пространство, если для любых
2-х его элементов
![]() определены
операции сложения
определены
операции сложения
![]() и
умножения на действительное число
и
умножения на действительное число
![]() ;
;
![]() со
свойствами:
1.
со
свойствами:
1.
![]() 2.
2.
![]() 3.
3.
![]() 4.
4.
![]() 5.
5.
![]() 6.
6.
![]() При
проверке аксиом получим: для множества
натуральных чисел, множества всех
положительных иррациональных чисел и
множества всех отрицательных рациональных
чисел не выполняется шестая аксиома.
При
проверке аксиом получим: для множества
натуральных чисел, множества всех
положительных иррациональных чисел и
множества всех отрицательных рациональных
чисел не выполняется шестая аксиома.
Тема:
Определение линейного пространства
Линейное
пространство
![]() обладает
следующим свойством:
обладает
следующим свойством:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Линейное
пространство обладает следующими
свойствами:
1) нейтральный элемент
![]() является
единственным;
2)
является
единственным;
2)
![]() для
любого
для
любого
![]() ;
3)
для любого
;
3)
для любого
![]() противоположный
элемент
противоположный
элемент
![]() является
единственным;
4)
является
единственным;
4)
![]() для
любого
для
любого
![]() ;
5)
;
5)
![]() для
любых
для
любых
![]() и
и
![]() .
.
Тема:
Умножение матриц
Соотношение
![]() выполняется,
только для …
выполняется,
только для …
|
|
|
|
перестановочных матриц |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Соотношение
![]() выполняется,
то такие матрицы называются перестановочными.
выполняется,
то такие матрицы называются перестановочными.
Тема:
Умножение матриц
Произведение
матрицы
![]() размерностью
32
на матрицу
размерностью
32
на матрицу
![]() существует,
если размерность матрицы
существует,
если размерность матрицы
![]() равна …
равна …
|
|
|
|
24 |
|
|
|
|
43 |
|
|
|
|
33 |
|
|
|
|
32 |
Решение:
Произведением
![]() матрицы
матрицы
![]() размера
размера
![]() на
матрицу
на
матрицу
![]() размера
размера
![]() называется
матрица
называется
матрица
![]() размера
размера
![]() ,
элемент которой
,
элемент которой
![]() равен
сумме произведений соответственных
элементов i-й
строки матрицы
равен
сумме произведений соответственных
элементов i-й
строки матрицы
![]() и
j-го
столбца матрицы
и
j-го
столбца матрицы
![]() ,
значит для того чтобы произведение
матриц существовало число столбцов
первой матрицы должно быть равно числу
строк второй.
,
значит для того чтобы произведение
матриц существовало число столбцов
первой матрицы должно быть равно числу
строк второй.
Тема:
Умножение матриц
Соотношение
![]() выполняется,
только для …
выполняется,
только для …
|
|
|
|
перестановочных матриц |
|
|
|
|
единичных матриц |
|
|
|
|
диагональных матриц |
|
|
|
|
нулевых матриц |
Решение:
Соотношение
![]() выполняется,
то такие матрицы называются перестановочными.
выполняется,
то такие матрицы называются перестановочными.
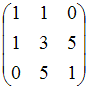
Тема: Умножение матриц Умножение матрицы A на матрицу B возможно, если эти матрицы имеют вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема:
Вычисление определителей
Корень
уравнения
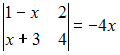 равен
…
равен
…
|
|
|
|
– 1 |
Тема:
Вычисление определителей
Определитель
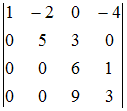 равен
…
равен
…
|
|
|
|
45 |
Решение:
Определитель
четвертого порядка можно вычислить,
например, разложением по элементам
первого столбца:
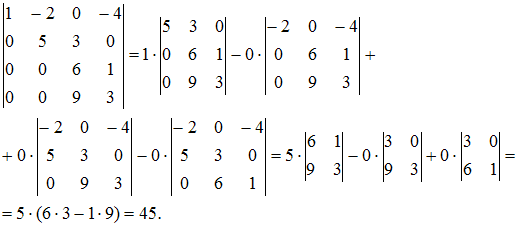
Тема:
Вычисление определителей
Определитель
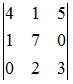 равен
…
равен
…
|
|
|
|
91 |
|
|
|
|
97 |
|
|
|
|
83 |
|
|
|
|
89 |
Решение:
Определитель
третьего порядка можно вычислить,
например, разложением по элементам
первой строки:
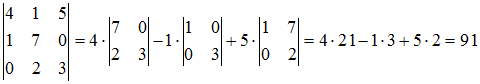 .
.
Тема:
Квадратичные формы
Матрице
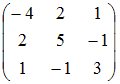 соответствует
квадратичная форма
соответствует
квадратичная форма
![]() ,
равная …
,
равная …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Слагаемые
из формы можно представить в виде
![]() .
Они соответствуют как i-строке и j-столбцу,
так и j-строке и i-столбцу матрицы в силу
того, что
.
Они соответствуют как i-строке и j-столбцу,
так и j-строке и i-столбцу матрицы в силу
того, что
![]() ,
поэтому на каждой из двух позиций ij
и ji
матрицы записывается по
,
поэтому на каждой из двух позиций ij
и ji
матрицы записывается по
![]() .
Соответственно, коэффициенты формы при
квадратах неизвестных, то есть
.
Соответственно, коэффициенты формы при
квадратах неизвестных, то есть
![]() ,
записываются на главной диагонали. Для
данной формы элементы матрицы равны:
,
записываются на главной диагонали. Для
данной формы элементы матрицы равны:
![]() Следовательно,
данная квадратичная форма имеет вид:
Следовательно,
данная квадратичная форма имеет вид:
![]()
Тема: Квадратичные формы Отрицательно определенная квадратичная форма может иметь вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Квадратичная
форма
![]() называется
отрицательно определенной, если при
всех значениях переменных
называется
отрицательно определенной, если при
всех значениях переменных ![]() ,
из которых хотя бы одно отлично от нуля,
,
из которых хотя бы одно отлично от нуля,
![]() .
1)
Для квадратичной формы
.
1)
Для квадратичной формы
![]() характеристическое
уравнение
характеристическое
уравнение
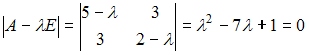 имеет
положительные корни
имеет
положительные корни
![]() Следовательно,
квадратичная форма
Следовательно,
квадратичная форма
![]() является
знакоположительной.
2) Для квадратичной
формы
является
знакоположительной.
2) Для квадратичной
формы
![]() характеристическое
уравнение
характеристическое
уравнение
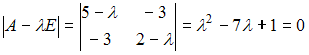 имеет
положительные корни
имеет
положительные корни
![]() Следовательно,
квадратичная форма
Следовательно,
квадратичная форма
![]() является
знакоположительной.
3) Для квадратичной
формы
является
знакоположительной.
3) Для квадратичной
формы
![]() характеристическое
уравнение
характеристическое
уравнение
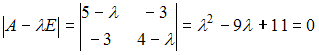 имеет
положительные корни
имеет
положительные корни
![]() Следовательно,
квадратичная форма
Следовательно,
квадратичная форма
![]() является
знакоположительной.
4) Для квадратичной
формы
является
знакоположительной.
4) Для квадратичной
формы
![]() характеристическое
уравнение
характеристическое
уравнение
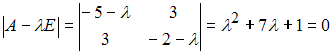 имеет
отрицательные корни
имеет
отрицательные корни
![]() Следовательно,
Следовательно,
![]() является
отрицательно определенной квадратичной
формой.
является
отрицательно определенной квадратичной
формой.
Тема: Квадратичные формы Положительно определенная квадратичная форма может иметь вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Квадратичная
форма
![]() называется
положительно (отрицательно) определенной,
если при всех значениях переменных
называется
положительно (отрицательно) определенной,
если при всех значениях переменных ![]() ,
из которых хотя бы одно отлично от нуля,
,
из которых хотя бы одно отлично от нуля,
![]()
![]() .
Для матрицы
.
Для матрицы
![]() характеристическое
уравнение
характеристическое
уравнение
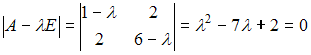 имеет
положительные корни
имеет
положительные корни
![]() Следовательно,
на основании критерия квадратичная
форма
Следовательно,
на основании критерия квадратичная
форма
![]() положительно
определенная.
положительно
определенная.
Тема:
Квадратичные формы
Матрице
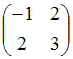 соответствует
квадратичная форма
соответствует
квадратичная форма
![]() ,
равная …
,
равная …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Слагаемые
из формы можно представить в виде
![]() .
Они соответствуют как i-строке и j-столбцу,
так и j-строке и i-столбцу матрицы в силу
того, что
.
Они соответствуют как i-строке и j-столбцу,
так и j-строке и i-столбцу матрицы в силу
того, что
![]() ,
поэтому на каждой из двух позиций ij
и ji
матрицы записывается по
,
поэтому на каждой из двух позиций ij
и ji
матрицы записывается по
![]() .
Соответственно коэффициенты формы при
квадратах неизвестных, то есть
.
Соответственно коэффициенты формы при
квадратах неизвестных, то есть ![]() ,
записываются на главной диагонали. Для
данной формы элементы матрицы
,
записываются на главной диагонали. Для
данной формы элементы матрицы
![]() .
Следовательно,
заданная квадратичная форма имеет вид
.
Следовательно,
заданная квадратичная форма имеет вид
![]() .
.
Тема:
Квадратичные формы
Канонический
вид квадратичной формы
![]() может
иметь вид …
может
иметь вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Приведем
квадратичную форму к каноническому
виду
![]() введем
замену
введем
замену
![]() и
и
![]() ,
получим канонический вид
,
получим канонический вид
![]() .
.
Тема:
Квадратичные формы
Матрица
квадратичной формы
![]() имеет
вид …
имеет
вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Матрица
квадратичной формы симметрична
относительно главной диагонали. Слагаемые
из формы можно представить в виде
![]() .
Они соответствуют как i-строке и j-столбцу,
так и j-строке и i-столбцу матрицы в силу
того, что
.
Они соответствуют как i-строке и j-столбцу,
так и j-строке и i-столбцу матрицы в силу
того, что
![]() ,
поэтому на каждой из двух позиций ij и
ji матрицы записывается по
,
поэтому на каждой из двух позиций ij и
ji матрицы записывается по
![]() .
Соответственно коэффициенты формы при
квадратах неизвестных, т.е.
.
Соответственно коэффициенты формы при
квадратах неизвестных, т.е. ![]() ,
записываются на главной диагонали. Для
данной формы элементы матрицы
,
записываются на главной диагонали. Для
данной формы элементы матрицы
![]()
![]() .
Следовательно,
заданная квадратичная форма описывается
матрицей
.
Следовательно,
заданная квадратичная форма описывается
матрицей
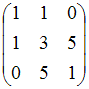 .
.
Тема: Квадратичные формы Квадратичная форма, не являющаяся знакоопределенной, может иметь вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Квадратичная
форма
![]() называется
положительно (отрицательно) определенной,
если при всех значениях переменных
называется
положительно (отрицательно) определенной,
если при всех значениях переменных ![]() ,
из которых хотя бы одно отлично от нуля,
,
из которых хотя бы одно отлично от нуля,
![]()
![]() .
1)
Для квадратичной формы
.
1)
Для квадратичной формы
![]() характеристическое
уравнение
характеристическое
уравнение
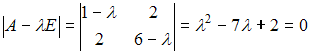 имеет
положительные корни
имеет
положительные корни
![]() Следовательно,
квадратичная форма
Следовательно,
квадратичная форма
![]() является
знакоположительной.
2) Для квадратичной
формы
является
знакоположительной.
2) Для квадратичной
формы
![]() характеристическое
уравнение
характеристическое
уравнение
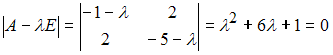 имеет
отрицательные корни
имеет
отрицательные корни
![]() .
Следовательно, квадратичная форма
.
Следовательно, квадратичная форма
![]() является
знакоотрицательной.
3) Для квадратичной
формы
является
знакоотрицательной.
3) Для квадратичной
формы
![]() характеристическое
уравнение
характеристическое
уравнение
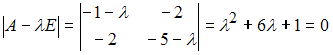 имеет
отрицательные корни
имеет
отрицательные корни
![]() .
Следовательно, квадратичная форма
.
Следовательно, квадратичная форма
![]() является
знакоотрицательной.
4) Для квадратичной
формы
является
знакоотрицательной.
4) Для квадратичной
формы
![]() характеристическое
уравнение
характеристическое
уравнение
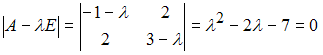 имеет
положительные корни
имеет
положительные корни
![]() .
Следовательно, квадратичная форма
.
Следовательно, квадратичная форма
![]() не
является знакоопределенной.
не
является знакоопределенной.





















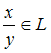 ,
для любых
,
для любых



























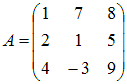 и
и
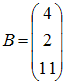

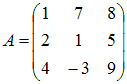 и
и

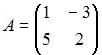 и
и

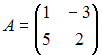 и
и