Математика

JJG

JG

a3

JJG

a3

JJG

a2

a2

JG

G

a1

a1

правая

левая

При перестановке местами двух соседних векторов ориентация тройки ме-

няется.

G

G

G

G

G

G G

G

Если тройки { a

,b , c }, {b , c , a }, { c , a ,b } - правые, то { a

, c , b }, { c , b , a },

G

G

G

{b

, a

, c } - левые.

При круговой (циклической) перестановке векторов ориентация тройки не

меняется.

Векторное произведение векторов

G

Векторным

произведением

вектора

a

на

вектор b называется

вектор

G

G

G

G

G

G

b

×b

c = a,

= a

= a ×b , удовлетворяющий следующим трем требованиям:

G

G

G

1). Длина вектора c равна произведению длин векторов a

и b на синус уг-

ла между ними, т.е.

G

=

G

=

G

G

G G

c

a

×b

a

b

sin (a,b).

2). Вектор cG

ортогонален

к каждому

из векторов

a и b , т.е.GcG

перпендикулярен плоскости, в которой лежат векторы a и b .

3). Вектор cG

направлен так, что тройка a b c является правой.

Алгебраические и геометрические свойства векторного произведения:

1°. aG×bG = − bG×aG . 2. αaG×bG =α aG×bG .

3. aG+bG×cG =[aG×cG]+ bG×cG .

4. [aG×aG]= 0G для любого вектора a .

5. Площадь параллелограммаG , построенного

на векторах aG и b как на сторонах,

Sпар = aG×bG .

6. [aG×bG] = 0 aG коллинеарен b .

151

Выражение векторного произведения

через декартовы координаты сомножителей

Если aG

={x1,

y1,

z1}, bG

={x2 ,

y2 , z2}, то

iG

Gj

G

G

G

={y z

} =

k

− z y

, z x

− x z

, x y

− y x

x

y

z

.

c

= a

×b

2

2

2

1

1 2

1

1 2

1

1 2

1

1

1

x2

y2

z2

iG×iG = Gj × Gj = k ×kG =0, iG× Gj =−Gj ×iG =iG×kG = − kG×iG = −Gj, Gj ×kG = − kG× Gj = iG.

	Если aG = (x1, y1, z1 ) и bG = (x2 , y2 , z2 ) коллинеарны, то	x1	=	y1
		x2		y2

kG,

=z1 . z2

Смешанное произведение векторов

Смешанное произведение некомпланарных векторов aGb cG = ( aG×bG cG)

по абсолютной величине равно объему параллелепипеда, построенного на этих
векторах, приведенных к одному началу, aGb cG											положительно, если тройка a , b ,
G
c правая и отрицательно, если она левая.
Если же векторы					G		G			G
					a ,		b ,			c компланарны, то a b c
	G GG	=		x1	y1		z1			= 0 .
равно нулю: a b c				x	y	2	z	2
				2
( aG×bG				x3	y3		z3
	cG)= ( bG×cG aG)								= ([cG×aG] bG), b aGcG = aGGc bG = cGbGaG = −aGbGcG.
( aG×bG	cG)= ( bG×cG aG)= (aG bG×cG ).

Смешанное произведение зависит от порядка сомножителей, но не зависит от того, какие сомножители связаны первичным знаком векторного произ-

веденияG.

G

G

G G

G

G

G

G

G

Если a = x1i

+ y1 j

+ z1k , b = x2i

+ y2 j

+ z2k

, c

= x3i + y3 j

+ z3k , то

G GG

=

x1

y1

z1

.

a b c

x

y

2

z

2

2

x3

y3

z3

152

II. Аналитическая геометрия в пространстве

Плоскость в пространстве

1.Ax + By + Cz + D = 0 - общее уравнение плоскости в декартовой системе

A2 + B2 + C 2 ≠ 0

координат;

2.

- уравнение плоскости, проходящей через

A(x − x0 ) + B( y − y0 ) +C(z − z0 ) = 0

перпендикулярной вектору nG ={A, B,C} ;

заданную точку (x0 , y0 , z0 )

и

3.

x

+

y

+

z

=1, abc ≠ 0

-

уравнение плоскости, отсекающей на осях ко-

a

b

c

ординат Ox , Oy , Oz отрезки a, b и c соответственно;

4.

- нормальное уравнение плоскости, где

x cosα + y cos β + z cosγ − p = 0

р – расстояние от начала координат до плоскости, а единичный вектор,

перпендикулярный плоскости, имеет координаты {cosα,cos β,cosγ};

5.	Ax + By + Cz + D = 0		- нормальный вид общего уравнения плоскости
	±	A2 + B2 + C 2

(знак нормирующего множителя противоположен знаку D);

6.	d = Ax0	+ By0 + Cz0 + D	- расстояние от точки (x0 , y0 , z0 )	до плоскости, за-
		A2 + B2 +C 2
	данной общим уравнением;

7.		x − x1	y − y1	z − z1		- уравнение плоскости, проходящей через три
		x2 − x1	y2 − y1	z2 − z1	= 0
		x3 − x1	y3 − y1	z3 − z1
						не лежащие на одной прямой;
	точки (xi , yi , zi ) (i=1,2,3),

	8.	cosϕ =	A1 A2 + B1 B2 + C1C2				- угол ϕ между плоскостями
			+ B2	+C 2	A2	+ B2
		A2					+ C 2
		1	1	1	2	2	2
		Ai x + Bi y +Ci z + Di = 0			( i =1,2) ;

9.		A1	=	B1		=	C1			- необходимое и достаточное условие параллельности плос-
		A		B	2		C	2
		2

костей Ai x + Bi y +Ci z = 0 (i =1,2);

153

10.A1 A2 + B1 B2 + C1C2 = 0 - необходимое и достаточное условие перпен-

дикулярности плоскостей Ai x + Bi y +Ci z = 0 (i =1,2) ;

11.

d =

D1 − D2

- расстояние между двумя параллельными плос-

A2 + B2

+C 2

и Ax + By + Cz + D2 = 0 .

костями Ax + By +Cz + D1 = 0

Прямая в пространстве

12.

A x

+ B y + C z + D = 0

- общее уравнение прямой как линии пере-

1

1

1

1

A2 x + B2 y + C2 z + D2 = 0

сечения

двух параллельных плоскостей;

13.

x − x0

=

y − y0

=

z −z0

- канонические уравнения прямой, проходя-

l

щей

m

n

и имеющей направляющий вектор с компонен-

через точку (x0 , y0 , z0 )

тами {l, m, n} ;

mx

−ly + (ly0 − mx0 )= 0

14.

ny − mz + (mz0 − ny0 )= 0 - уравнения прямой в виде проекций на

− nx0 )= 0

nx −lz + (lz0

координатные плоскости;

x = x0 +lt

15.

- параметрические уравнения прямой, проходящей

y = y0 + mt

z = z0 + nt

через точку (x0 , y0 , z0 ) и имеющей направляющий вектор с компонентами

{l, m, n} ;

l = B1C2

16. m = C1 A2

n = A1 B2

− B2C1

−C2 A1 - соотношения между компонентами направ-

− A2 B1

ляющего вектора прямой и координатами общего уравнения прямой;

17.			x − x1	=	y − y1	=	z −z1		- канонические уравнения прямой, про-
							z2 − z1
			x2 − x1		y2 − y1
	ходящей через точки с координатами (xi , yi , zi ) (i =1, 2 );

154

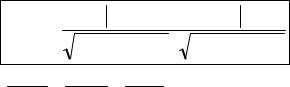
18.

cosϕ =

l1l2

+ m1m2 + n1n2

- косинус угла ϕ

между пря-

l 2

+ m2

+ n2

l 2

+ m2

+ n2

1

1

1

2

2

2

мыми

x − x0

=

y − y0

= z −z0

(i =1, 2 ), проходящими через точку (x0 , y0 , z0 ) ;

li

mi

ni

19.

l1

=

m1

=

n1

-

условие

параллельности

двух

прямых

l2

m2

n2

x − xi

=

y − yi

=

z − z

i

( i =1, 2 );

li

mi

ni

20.

-

условие перпендикулярности двух прямых

x − xi

l1l2 + m1m2 + n1n2

= 0

=

y − yi

=

z − z i

(i =1, 2 );

li

mi

ni

21.

Прямые: L

:

x − x1

=

y − y1

=

z − z1

и L :

x − x2

=

y − y2

=

z − z2

1

l1

m1

n1

2

l2

m2

n2

лежат в одной плоскости, если

x2 − x1

y2 − y1

z2 − z1

l1

m1

n1

= 0.

l2

m2

n2

Прямая и плоскость в пространстве

22.

A1 x + B1 y +C1 z + D1 + λ( A2 x + B2 y +C2 z + D2 ) = 0

−

уравнение пучка

плоскостей,

проходящих через прямую,

заданную

общим уравнением

A x + B y +C z + D =

0

1

1

1

1

A2 x + B2 y +C2 z + D2 = 0.

x = x0 +lt1 ,

Ax0 + By0 +Cz0 + D

23.

y = y0

+ mt1 ,

где

t1

= −

- координаты точки пере-

Al + Bm +Cn

z = z

0

+ nt

,

1

сечения прямой

x −

x

0

=

y − y

0

=

z −z

0

и плоскости Ax + By +Cz + D = 0 ;

l

m

n

155

24.		sin ϕ =				Al + Bm + Cn				- синус угла между прямой
					A2 + B2 + C 2			l 2 + m2 + n2
x − x0		=	y − y0		= z −z 0		и плоскостью Ax + By +Cz + D = 0 ;
l			m			n
25.		Al + Bm +Cn = 0						-	условие	параллельности	прямой
x − x0		=	y − y0		= z −z 0		и плоскости Ax + By +Cz + D = 0 ;
l			m			n
26.		A	= B =		C		-		условие	перпендикулярности	прямой
x − x		l	m		n
	0	=	y − y	0	=	z −z	0 и плоскости Ax + By +Cz + D = 0 .
l			m			n
III. Аналитическая геометрия на плоскости

Прямая на плоскости

1. d = (x − x )2		+ ( y	2	− y )2
2	1			1

x = x1 + λ x2 ,

1+ λ

2.y = y1 + λ y2 ,

1 + λ

λ≠ −1

x= x1 +2 x2 ;

3.y = y1 +2 y2

x1 y1 1

4. x2 y2 1 = 0 x3 y3 1

-расстояние между точками

A(x1,y1) и B (x2,y2);

-координаты точки С (x,y), которая делит отрезок, соединяющий точки A(x1,y1) и

B(x2,y2), в отношении λ = CBAC ;

-координаты середины отрезка АВ;

-условие принадлежности трёх точек

(x1,y1), (x2,y2), (x3,y3) одной прямой;

156

	S = 1						x1	y1		1
							x	y	2	1		=
			2				2
5.							x3	y3		1
	=	1		x2 − x1					y2 − y1
		2		x			− x		y	− y
				3			1		3		1

6.A x+B y+C = 0

7.A (x - x0)+B (y - y0) = 0

8.x −l x0 = y −my0

x = x0 +lt,

9.y = y0 + mt, t ( −∞,∞)

10.		y − y1			=	x − x1
		y	2	− y		x	− x
				1	2		1

y = kx + b,

11.k = tgα

12.ax + by =1,

a ≠ 0, b ≠ 0

13.x cosα + y sinα − p = 0

14.Ax + By +C = 0

±A2 + B2

-площадь треугольника с вершинами

(x1,y1), (x2,y2), (x3,y3).

-общее уравнение прямой;

-уравнение прямой, проходящей через

точку (x0,y0) перпендикулярно нормальному вектору {A,B};

-каноническое уравнение прямой,

проходящей через точку (x0,y0) параллельно вектору {l,m};

-параметрические уравнения прямой, проходящей через точку (x0,y0)

параллельно вектору {l,m};

-уравнение прямой, проходящей через две заданные точки (x1,y1) и (x2,y2);

-уравнение прямой с угловым

	π		π			-
коэффициентом k, где α 0,	2			2	, π

угол наклона прямой к оси ox;

-уравнение прямой в отрезках, где (а,0) и (0,b) - координаты точек пересечения прямой

сосями Ox и Oy;

-нормальное уравнение прямой,

где р - расстояние от начала координат до прямой, α - угол между осью Ox и перпендикуляром к прямой, проходящим через начало координат;

- нормальный вид общего уравнения прямой; знак нормирующего множителя противоположен знаку С;

157

15. d = Ax0 + By0 +C

A2 + B2

- расстояние от точки (x0,y0) до прямой

Ax + By + C = 0;

B1

C1

B2

C2

x

=

,

A1

B1

0

16.

A2

B2

C1

A1

C2

A2

y

=

0

A1

B1

A2

B2

b

−b

x0

=

2

1

,

17.

k1 − k2

y

=

b2 k1 −b1k2

0

k1 − k2

- координаты точек пересечения двух прямых

A1x + B1y + C1 = 0 и A2x + B2y + C2 = 0;

- координаты точек пересечения прямых y = k1x + b1 и y = k2x + b2;

18.A1 B2 − A2 B1 = 0, k1 = k2

19.A1 A2 + B1 B2 = 0, k1k2 = −1

-условия параллельности прямых, заданных

вобщем виде: A1 x + B1 y + C1 = 0, A2 x + B2 y + C2 = 0

и в виде y = k1 x + b1, y=k2 x + b2;

- условие перпендикулярности прямых, заданных в

общем виде A1 x + B1 y + C1 = 0, A2 x + B2 y + C2 = 0 и в виде y = k1 x + b1, y=k2 x+b2;

tgα =		A1B2 − A2 B1					,
		A A		+ B B
		1	2	1	2

20. tgα =		k1 − k2			,
	1 + k k		2
		1
k1k2 ≠ −1,
α = π ,		если k k				2	= −1.
2				1

21.	A1 x + B1 y + C1 +
	+λ( A x + B y + C			) = 0
	2	2	2

- угол α между двумя прямыми, заданными в

общем виде A1 x + B1 y + C1 = 0, A2 x + B2 y + C2 = 0 и в виде y=k1x+b1, y=k2x+b2;

- уравнение пучка прямых через точку М, если

A1 x + B1 y + C1 = 0 и A2 x + B2 y + C2 = 0 - уравнения двух прямых, пересекающихся в

точке М.

158

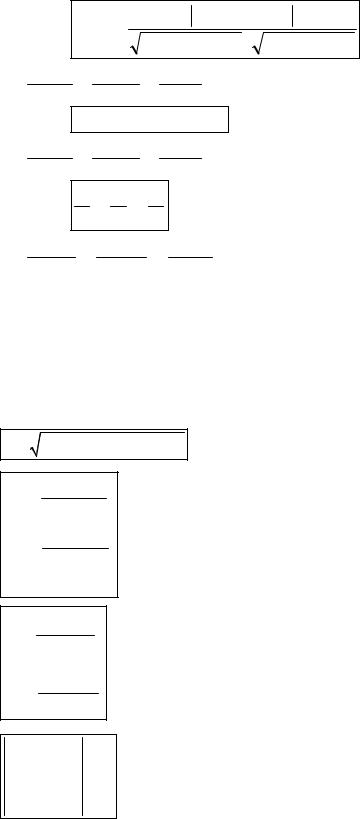
Кривые второго порядка

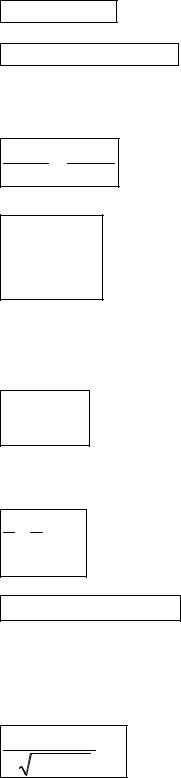
Эллипс

Эллипс - геометрическое место точек M (x, y), для которых сумма расстояний до двух заданных точек F1 (+c,0) и F2 (−c,0)

(называемых фокусами эллипса) постоянна и равна 2a .

JJJJG

JJJJJG

JJJJG

= 2c, a > c ,

F1M

+

F2M

=

2a и

F1F2

c2

= a2 −b2 ,

x2

+

y2

=1

- каноническое уравнение эллипса.

a2

b2

Эллипс – центральная линия второго порядка, замкнутая линия, симметричная относительно осей и центра. Элементами эллипса являются: точка О - центр эллипса; точки A, B, C, D - вершины эллипса; точки F1(с,0), F2(-с,0) - фокусы эллипса; 2c - фокусное расстояние, которое вычисляется по

формуле c = a2 −b2 ; АВ = 2а и CD = 2b - большая и малая оси эллипса; a и b -

большая и малая полуоси эллипса; e = ac , (e <1) - эксцентриситет эллипса,

	который вычисляется по формуле	e = 1−	b2	.
			a2

Эксцентриситет определяется отношением осей эллипса и характеризует его форму: чем больше e, тем более вытянут эллипс вдоль большой оси.

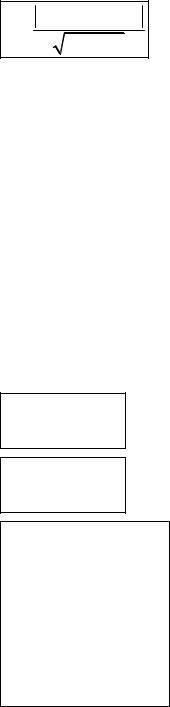
Прямые D1 и D2 , параллельные малой оси эллипса и отстоящие от его центра на расстояниях

d = ± a	, называются директрисами эллипса,
e

соответствующими фокусам F1 и F2.

Отношение расстояния любой точки эллипса до фокуса к расстоянию ее до

соответствующей директрисы постоянно и равно эксцентриситету			r1	=	r2		= e .
			d
					d	2
			1
	x = a cos t,	- параметрические уравнения эллипса, где t	-	параметр,
	y = bsin t

t [0,2π) ; (t - угол, образованный подвижным радиусом с положительным направлением оси Ox);

159

b2

ρ = a - уравнение эллипса в полярных координатах, связанных с

1 −ecosϕ

фокусом;

e = a2 −b2 - эксцентриситет эллипса, если координатные оси совпадают с a

осями эллипса.

Окружность

Окружность - геометрическое место точек, равноудаленных от точки О (центр).

x2 + y2 =R2 - уравнение окружности радиуса R с центром в

начале координат;

(x − x0 )2 + ( y − y0 )2 = R2 - уравнение окружности радиуса

R с центром в точке (x0,y0);

x = x0 + R cost, - параметрические уравнения окружности радиуса R с

y = y0 + Rsin t

центром в точке (x0,y0);

ρ = R - уравнение окружности радиуса R с центром в начале

координат в полярных координатах;

ρ2 −2ρρ0 cos(ϕ−ϕ0 ) +ρ02 = R2 - уравнение окружности радиуса

R с центром в точке ( ρ 0,ϕ0) в полярных координатах;

ρ = 2R cosϕ - уравнение окружности радиуса R в полярных

координатах. Центр окружности лежит на полярной оси, окружность касается начала координат.

Гипербола

Гипербола - геометрическое место точек M (x, y), для которых абсо-

лютная величина разности расстояний до двух заданных точек

F1 (+c,0) и F2 (−c,0) (называемых фокусами гиперболы) постоянна и равна 2a .

F1M − F2 M = 2a и F1F2 = 2c , a < c ,

c2 = a2 +b2 .

160