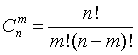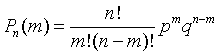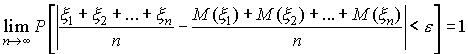13 Функции нескольких переменных

1. Определение. Если каждой паре (x,y) значений двух независимых переменных из области  ставится определенное значение z, то говорят, что z есть функция двух переменных (x,y).

   z=f(x,y)

2. Геометрическое изображение функции двух переменных - поверхность.

3. Частное и полное приращение функции.

Полное приращение функции

z=f(x+x, y+y)f(x,y)

Частное приращение функции

_x z=f(x+x)f(x,y)

_y z=f(x,y+y)f(x,y)

Вообще, полное приращение функции не равно сумме частных приращений.

Пример. z=xy.

_x z=(x+x)yxy=yx

_y z=x(y+y)xy=xy

z=(x+x)(y+y)xy=yx+xy+yx  _y z+_x z.

4. Непрерывность функции нескольких переменных

Предел функции.

Пусть z=f(x,y) определена в некоторой окрестности A(x₀,y₀).

Определение. Постоянное число b называют пределом z=f(x,y) при P(x,y) стремящемся к A, если для любого  > 0 можно указать такое значение  > 0, что для всех x, удовлетворяющих неравенству AP < , имеет место неравенство f(x,y)b < .

5. Непрерывная функция

6. Частные производные

8. § 6 Полный дифференциал функции нескольких переменных

9. Если функция дифференцируема в точке (zfxy=; ()Pxy000;, то ее полное при-ращение можно представить в виде

10. ()()()ΔΔΔfxyfxyxfxyyzyxy000000,,,=′+′++αβ .

11. Сумма двух первых слагаемых есть главная линейная (относительно Δx и ) часть приращения функции. Δy

12. Определение Если функция ()zfxy=; дифференцируема в точке , то главная, линейная относительно приращения аргументов, часть ее полного прира-щения называется (Pxy000; полным дифференциалом функции и обозначается

13. . (5)

14. Приращения независимых переменных называют дифференциалами независи-мых переменных х и у и обозначают соответственно и . Тогда полный диффе-ренциал функции записывается в виде dy

15. ()()()dzdfxyfxyxdxfxyydyPdef0000000==+,,,∂∂∂∂

16. Выражения ()()∂∂∂∂ fxyxdxfxyydy0000,,, называют частными дифференциалами функции и обозначают и . Тогда (zfxy=; dfxdfy

17. dzdzdzxy=+.

18. Определение полного дифференциала легко обобщается на случай функции любого числа аргументов. Например для случая трех переменных

19. ()()()zzyxfyzyxfxzyxfudzyxPΔ′+Δ′+Δ′=000000000,,,,,,.

20. Из определения дифференциала функции нескольких переменных следует, что

21. ()()()zfxyfxydfxy=⇒≈,, Δ0000 ,

22. ()()()ufxyzfxyzdfxyz=⇒≈,,,,,, Δ000000,

23. ()()()ufPPRfPdfPn=∈⇒≈, Δ00.

24. Эти соотношения позволяют получить формулы для приближенного вычисления зна-чений функции:

25. ()()()fxxyyfxydfxy000000++≈+ΔΔ,, ,

26. ()()()fxxyyzzfxyzdfxyz0000000+++≈+ΔΔΔ,,,,,, .

27. В общем случае

28. ()()()()fPfPdfPPOPRrn≈+∀∈⊂000 . (6)

29. 2,03). 241

30. Точка Р расположена достаточно близко от точки ()P012;, Δx=0,02Δy=0,03. По формуле (6) имеем

31. ()fPxyP0262222==+ .

32. ()()dfPfxxfyyxyPPxyxyP02200222204220,022220,038,872=+=⋅⋅+⋅≈++∂∂∂∂ ΔΔlnln

33. Следовательно

34. ()()()fPfdf≈+≈+=1212648,87272,872;;.

35. Оценим погрешность вычислений. Точное значение, вычисленное с помощью калькулятора . ()fP=73583,

36. Абсолютная погрешность

37. Δf=−=7358372,8720,711,.

38. Относительная погрешность

39. ()δfffxy=⋅==Δ,,100%0,711735830,96%

40. Описанный в примере алгоритм вычислений основан на замене приращения функции ее полным дифференциалом.

41. Полный дифференциал используется главным образом для оценки погрешно-стей вычислений по формулам.

42. Пусть задана дифференцируемая функция n переменных: ()ufxxxn=12,,...,. Тогда аб-солютная погрешность вычислений по этой формуле оценивается величиной Δu

43. ΔΔΔuuxxuxxuxxnn=+++∂∂∂∂∂∂ 1122... ,

44. относительная погрешность - величиной

45. δuuu=Δ.

Достаточные условия локального экстремума

В предыдущих примерах мы видели, что хотя необходимое условие не гарантировало наличие экстремума в критической точке, мы смогли исследовать поведение функции в окрестности этой точки и выяснить, имеется ли в ней экстремум и если да, то какого рода. Однако для выяснения этого нам пришлось иной раз прибегать к искусственным преобразованиям функции, которые во общем случае могут быть не очевидны или затруднительны. В данном разделе мы рассмотрим несколько общих теорем, позволяющих исследовать поведение функции в критической точке.

        Теорема 7.5   Пусть  -- критическая точка функции . Если функция не убывает в некоторой левой окрестности точки и не возрастает в некоторой её правой окрестности , то точка  -- точка локального максимума.

Если же функция не возрастает в некоторой левой окрестности и не убывает в некоторой правой окрестности , то точка  -- точка локального минимума.

        Доказательство.     Если не убывает в , то при всех , поскольку из непрерывности . Точно так же, при всех . Выберем из чисел и наименьшее: и рассмотрим симметричную окрестность . При , очевидно, , то есть  -- точка локального максимума.

Вторая половина утверждения теоремы сводится к первой, если положить и заметить, что функция не убывает в и не возрастает в ; локальный максимум функции соответствует локальному минимуму функции  .     

        Замечание 7.4   Найденное достаточное условие локального экстремума гарантирует наличие экстремума в точке . Однако оно не является необходимым: можно найти такую функцию , которая имеет экстремум (например, минимум) в некоторой точке , однако не монотонна ни в какой левой окрестности и ни в какой правой окрестности этой точки. Примером может служить функция

График этой функции зажат между двумя параболами и и в окрестности точки 0 имеет бесконечно много промежутков монотонности, разделённых стационарными точками, так что не монотонна ни на каком интервале вида или . В точке 0 функция непрерывна (по теореме "о двух милиционерах") и имеет минимум, так как при всех .

Заметим кстати, что производная этой функции равна

Эта производная имеет в точке разрыв второго рода.     

        Теорема 7.6   Пусть  -- критическая точка функции , и у этой функции существует производная в некоторой проколотой окрестности . Если при этом в левой окрестности имеет место неравенство , а в правой окрестности  -- неравенство , то точка  -- точка локального максимума; если же в левой окрестности выполнено неравенство , а в правой окрестности -- неравенство , то точка  -- точка локального минимума. Наконец, если производная в левой и в правой окрестности имеет один и тот же знак, то точка не является точкой локального экстремума.

        Доказательство.     Доказательство первых двух утверждений теоремы сразу же следует из предыдущей теоремы и теоремы 7.2 о связи знака производной с возрастанием и убыванием функции: из неравенства следует неубывание функции , а из неравенства  -- её невозрастание. Последнее утверждение теоремы также очевидно.     

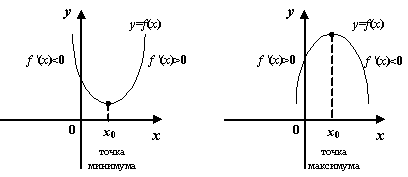
Рис.7.25.Связь смены знака производной с локальными экстремумами

Доказанную теорему можно сформулировать следующим образом:

если производная меняет знак с на при переходе через критическую точку , то в этой точке -- локальный максимум функции ; если знак производной меняется с на , то в точке  -- локальный минимум; если же знак производной при переходе через не изменяется, то локального экстремума в точке функция не имеет.

Следующая теорема позволяет обойтись для обнаружения экстремума исследованием функции только в точке (а не в её окрестности, как предыдущие теоремы), но зато требует привлечения второй производной.

        Теорема 7.7   Пусть  -- стационарная точка функции , и в этой точке существует вторая производная , причём . Тогда при точка есть точка локального максимума, а при  -- локального минимума.

        Доказательство.     Поскольку , то по определению производной

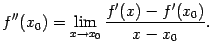
Пусть . Тогда из существования предела следует, что для любого из некоторой достаточно малой проколотой окрестности точки выполняется то же неравенство для допредельного выражения, то есть

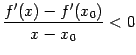
при . Поскольку, по предположению теоремы,  -- стационарная точка, то , откуда , то есть имеет знак, противоположный знаку : при и при . Остаётся лишь применить теперь предыдущую теорему, из которой следует, что  -- точка локального максимума.

Доказательство для случая совершенно аналогично.     

Экстремум функции и необходимое условие экстремума

Напомним определение локального экстремума функции.

        Определение 7.4   Пусть функция определена в некоторой окрестности , , некоторой точки своей области определения. Точка называется точкой локального максимума, если в некоторой такой окрестности выполняется неравенство ( ), и точкой локального минимума, если .     

Понятия локальный максимум и локальный минимум объединяются термином локальный экстремум.

Следующая теорема даёт необходимое условие того, чтобы точка была точкой локального экстремума функции .

        Теорема 7.4   Если точка  -- это точка локального экстремума функции , и существует производная в этой точке , то .

Доказательство этой теоремы сразу же следует из теоремы Ферма (см. гл. 5).    

Утверждение теоремы можно переформулировать так:

если функция имеет локальный экстремум в точке , то либо 1) , либо 2) производная не существует.

Точка называется критической точкой функции , если непрерывна в этой точке и либо , либо не существует. В первом случае (то есть при ) точка называется также стационарной точкой функции .

Итак, локальный экстремум функции может наблюдаться лишь в одной из критических точек этой функции.

        Пример 7.18   Рассмотрим функцию . Её производная существует при всех и равна . Следовательно, все критические точки -- стационарные и задаются уравнением . Это уравнение можно записать в виде ; оно имеет единственный корень : это единственная стационарная точка. Записав функцию в виде , легко увидеть, что в стационарной точке функция имеет минимум, равный .     

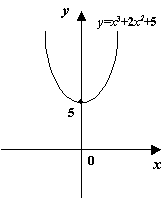
Рис.7.21.График функции

1. Случайные события. Частота. Вероятность.    Теория вероятностей — математическая наука, изучающая закономерности массовых случайных явлений (событий).     Случайным событием (или просто событием) называется всякое явление, которое может произойти или не произойти при осуществлении определенной совокупности условий. Теория вероятностей имеет дело с такими событиями, которые имеют массовый характер. Это значит, что данная совокупность условий может быть воспроизведена неограниченное число раз. Каждое такое осуществление данной совокупности условий называют испытанием (или опытом).     Если, например, испытание состоит в бросании монеты, то выпадение герба является событием; если испытание — изготовление подшипника данного типа, то соответствие подшипника стандарту — событие; если испытание — бросание игральной кости, т. е. кубика, на гранях которого проставлены цифры (очки) от 1 до 6, to выпадение пятерки — событие.     События будем обозначать заглавными буквами латинского алфавита: A, В, С, ... .     Пусть при n испытаниях событие A появилось m раз.     Отношение m/n называется частотой (относительной частотой) события A и обозначается Р*(А)=m/n     Опыт показывает, что при многократном повторении испытаний частота Р*(А) случайного события обладает устойчивостью. Поясним это на примере.     Пусть при бросании монеты 4040 раз герб выпал 2048 раз. Частота появления герба в данной серии опытов равна Р*(А)=m/n=2048/4040=0,5069. При бросании той же монеты 12000 раз герб выпал 6019 раз. Следовательно, в этом случае частота Р*(А)=6019/12000=0,5016. Наконец, при 24000 бросаний герб появился 12012 раз с частотой Р*(А)=0,5005. Таким образом, мы видим, что при большом числе бросаний монеты частота появления герба обладает устойчивостью, т. е. мало отличается от числа 0,5. Как показывает опыт, это отклонение частоты от числа 0,5 уменьшается с увеличением числа испытаний. Наблюдаемое в этом примере свойство устойчивости частоты является общим свойством массовых случайных событий, а именно, всегда существует такое число, к которому приближается частота появления данного события, мало отличаясь от него при большом числе испытаний. Это число называется вероятностью события. Оно выражает объективную возможность появления события. Чем больше вероятность события, тем более возможным оказывается его появление. Вероятность события A будем обозначать через Р(А). В рассмотренном выше примере вероятность появления герба, очевидно, равна 0,5.     Событие называется достоверным, если оно в данном опыте обязательно должно произойти; наоборот, событие называется невозможным, если оно в данном опыте не может произойти.     Пусть, например, из урны, содержащей только черные шары, вынимают шар. Тогда появление черного шара — достоверное событие; появление белого шара — невозможное событие.     Если событие достоверно, то оно произойдет при каждом испытании (m=n). Поэтому частота достоверного события всегда равна единице. Наоборот, если событие невозможно, то оно ни при одном испытании не осуществится (m=0). Следовательно, частота невозможного события в любой серии испытаний равна нулю. Поэтому вероятность достоверного события равна единице, а вероятность невозможного события равна нулю.     Если событие A не является ни достоверным, ни невозможным, то его частота m/n при большом числе испытаний будет мало отличаться от некоторого числа p (где 0 < p < 1 ) — вероятности события A.     Совмещением (или произведением) двух событий A и В называется событие, состоящее в совместном наступлении как события A, так и события В. Это событие будем обозначать АВ или ВА.     Аналогично, совмещением нескольких событий, например A, В и С, называется событие D=ABC, состоящее в совместном наступлении событий A, В и С.     Объединением (или суммой) двух событий A и В называется событие С, заключающееся в том, что произойдет по крайней мере одно из событий A или В. Это событие обозначается так: С=А+В.     Объединением нескольких событий называется событие, состоящее в появлении по крайней мере одного из них. Запись D=A+B+C означает, что событие D есть объединение событий A, В и С.     Два события A и В называются несовместными, если наступление события A исключает наступление события В. Отсюда следует, что если события A и В несовместны, то событие AB — невозможное.

   Рассмотрим следующий пример. Будем следить за движением какой-нибудь определенной молекулы газа, заключенного в некоторый объем. Внутри этого объема выделим объемы и , частично перекрывающие друг друга (рис. 1). Пусть событие A — попадание молекулы в объем , событие В — попадание молекулы в объем . Совмещением событий A и В является попадание молекулы в общую часть объемов и . Если объемы и не имеют общих точек, то ясно, что события A и В несовместны. Объединением событий A и В является попадание молекулы или только в объем или только в объем , или же в их общую часть.

§ 2. ПОСЛЕДОВАТЕЛЬНЫЕ ИСПЫТАНИЯ. ФОРМУЛА БЕРНУЛЛИ.    Предположим, что производится n независимых испытаний, в результате каждого из которых может наступить или не наступить некоторое событие A. Пусть при каждом испытании вероятность наступления события А равна P(A)=p и, следовательно, вероятность противоположного события (ненаступления А) равна . Определим вероятность Pn(m) того, что событие А произойдет m раз при n испытаниях. При этом заметим, что наступления или ненаступления события А могут чередоваться различным образом. Условимся записывать возможные результаты испытаний в виде комбинаций букв А и . Например, запись означает, что в четырех испытаниях событие осуществилось в 1-м и 4-м случаях и не осуществилось во 2-м и 3-м случаях.    Всякую комбинацию, в которую А входит m раз и входит n-m раз, назовем благоприятной. Количество благоприятных комбинаций равно количеству k способов, которыми можно выбрать m чисел из данных n; таким образом, оно равно числу сочетаний из n элементов по m, т.е.

   Подсчитаем вероятности благоприятных комбинаций. Рассмотрим сначала случай, когда событие A происходит в первых m испытаниях и, следовательно, не происходит в остальных n-m испытаниях. Такая благоприятная комбинация имеет следующий вид:

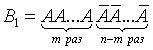
   Вероятность этой комбинации в силу независимости испытаний (на основании теоремы умножения вероятностей) составляет

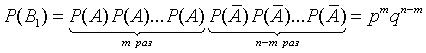
   Так как в любой другой благоприятной комбинации Вi событие A встречается также m раз, а событие происходит n-m раз, то вероятность каждой из таких комбинаций также равна . Итак

   Все благоприятные комбинации являются, очевидно, несовместными. Поэтому (на основании аксиомы сложения вероятностей)

   Следовательно,

(13)

или, так как

, то

(13')

   Формула (13) называется формулой Бернулли *.    Пример 1. Вероятность попадания в цель при одном выстреле равна 0,6. Какова вероятность того, что 8 выстрелов дадут 5 попаданий? (Решение)    Часто необходимо знать, при каком значении m вероятность принимает наибольшее значение, т. е. требуется найти наивероятнейшее число наступления события A в данной серии опытов. Можно доказать, что число должно удовлетворять двойному неравенству

(14)

   Заметим, что сегмент [np-q;np+p], в котором лежит , имеет длину (np+p)-(np-q)=p+q=1. Поэтому, если какой-либо из его концов не является целым числом, то между этими концами лежит единственное целое число, и определено однозначно. В том случае, если оба конца — целые числа, имеются два наивероятнейших значения: np-q и np+p.    Пример 2. Определить наивероятнейшее число попаданий в цель в примере 1. (Решение)    При больших значениях n подсчет вероятностей Pn(m) по формуле (13) связан с громоздкими вычислениями. В этом случае удобнее пользоваться следующей формулой:

(15)

, где

(p не равно нулю и единице), a

   Формула (15) выражает так называемую локальную теорему Лапласа **. Точность этой формулы повышается с возрастанием n.    Функция , как мы увидим в дальнейшем, играет очень большую роль в теории вероятностей. Ее значения при различных значениях аргумента приведены в Приложении (см. табл. I).    Пример 3. Игральную кость бросают 80 раз. Определить вероятность того, что цифра 3 появится 20 раз. (Решение)

§ 3. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ    Понятие случайной величины является основным в теории вероятностей и ее приложениях. Случайными величинами, например, являются число выпавших очков при однократном бросании игральной кости, число распавшихся атомов радия за данный промежуток времени, число вызовов на телефонной станции за некоторый промежуток времени, отклонение от номинала некоторого размера детали при правильно налаженном технологическом процессе и т. д.    Таким образом, случайной величиной называется переменная величина, которая в результате опыта может принимать то или иное числовое значение.    В дальнейшем мы рассмотрим два типа случайных величин — дискретные и непрерывные.    1. Дискретные случайные величины.    Рассмотрим случайную величину * , возможные значения которой образуют конечную или бесконечную последовательность чисел x1, x2, ..., xn, ... . Пусть задана функция p(x), значение которой в каждой точке x=xi (i=1,2, ...) равно вероятности того, что величина примет значение xi

(16)

   Такая случайная величина называется дискретной (прерывной). Функция р(х) называется законом распределения вероятностей случайной величины, или кратко, законом распределения. Эта функция определена в точках последовательности x1, x2, ..., xn, ... . Так как в каждом из испытаний случайная величина принимает всегда какое-либо значение из области ее изменения, то

   Пример 1. Случайная величина — число очков, выпадающих при однократном бросании игральной кости. Возможные значения — числа 1, 2, 3, 4, 5 и 6. При этом вероятность того, что примет любое из этих значений, одна и та же и равна 1/6. Какой будет закон распределения ? (Решение)    Пример 2. Пусть случайная величина - число наступления события A при одном испытании, причем P(A)=p. Множество возможных значений состоит из 2-х чисел 0 и 1: =0, если событие A не произошло, и =1, если событие A произошло. Таким образом,

   Предположим, что производится n независимых испытаний, в результате каждого из которых может наступить или не наступить событие A. Пусть вероятность наступления события A при каждом испытании равна p. Рассмотрим случайную величину — число наступлений события A при n независимых испытаниях. Область изменения состоит из всех целых чисел от 0 до n включительно. Закон распределения вероятностей р(m) определяется формулой Бернулли (13'):

   Закон распределения вероятностей по формуле Бернулли часто называют биномиальным, так как Pn(m) представляет собой m-й член разложения бинома .    Пусть случайная величина может принимать любое целое неотрицательное значение, причем

(17)

   где — некоторая положительная постоянная. В этом случае говорят, что случайная величина распределена по закону Пуассона, Заметим, что при k=0 следует положить 0!=1.    Как мы знаем, при больших значениях числа n независимых испытаний вероятность Pn(m) наступления m раз события A удобнее находить не по формуле Бернулли, а по формуле Лапласа [см. формулу (15)]. Однако последняя дает большие погрешности при малой вероятности р появления события А в одном испытании. В этом случае для подсчета вероятности Pn(m) удобно пользоваться формулой Пуассона, в которой следует положить .    Формулу Пуассона можно получить как предельный случай формулы Бернулли при неограниченном увеличении числа испытаний n и при стремлении к нулю вероятности .    Пример 3. На завод прибыла партия деталей в количестве 1000 шт. Вероятность того, что деталь окажется бракованной, равна 0,001. Какова вероятность того, что среди прибывших деталей будет 5 бракованных? (Решение)    Распределение Пуассона часто встречается и в других задачах. Так, например, если телефонистка в среднем за один час получает N вызовов, то, как можно показать, вероятность Р(k) того, что в течение одной минуты она получит k вызовов, выражается формулой Пуассона, если положить .

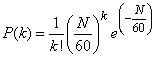
   Если возможные значения случайной величины образуют конечную последовательность x1, x2, ..., xn, то закон распределения вероятностей случайной величины задают в виде следующей таблицы, в которой

и

 

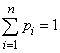
Значения	x1	x2	...	xn
Вероятности p(xi)	p1	p2	...	pn

    Эту таблицу называют рядом распределения случайной величины . Наглядно функцию р(х) можно изобразить в виде графика. Для этого возьмем прямоугольную систему координат на плоскости.    По горизонтальной оси будем откладывать возможные значения случайной величины , а по вертикальной оси - значения функции . График функции р(х) изображен на рис. 2. Если соединить точки этого графика прямолинейными отрезками, то получится фигура, которая называется многоугольником распределения.

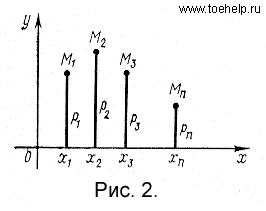
   Пример 4. Пусть событие А — появление одного очка при бросании игральной кости; Р(A)=1/6. Рассмотрим случайную величину — число наступлений события А при десяти бросаниях игральной кости. Значения функции р(х) (закона распределения) приведены в следующей таблице:  

Значения	0	1	2	3	4	5	6	7	8	9	10
Вероятности p(xi)	0,162	0,323	0,291	0,155	0,054	0,013	0,002	0	0	0	0

   Вероятности p(xi) вычислены по формуле Бернулли при n=10. Для x>6 они практически равны нулю. График функции p(x) изображен на рис. 3.

5. ЗАКОНЫ БОЛЬШИХ ЧИСЕЛ.    2. Закон больших чисел Чебышева.    Имеет место следующее утверждение. Пусть - последовательность попарно независимых случайных величин, имеющих ограниченные в совокупности дисперсии, т. е. для любого i. Тогда, каково бы нибыло , справедливо соотношение

(54)

   (Доказательство)    Смысл закона больших чисел Чебышева состоит в следующем. В то время как отдельная случайная величина может принимать значения, очень далекие от своего математического ожидания, средняя арифметическая большого числа случайных величин с вероятностью, близкой к единице, принимает значение, мало отличающееся от среднего арифметического их математических ожиданий.    Частный случай закона больших чисел Чебышева. Пусть - последовательность попарно независимых случайных величин, имеющих ограниченные в совокупности дисперсии, т. е. и одинаковые математические ожидания . Тогда, каково бы нибыло , справедливо соотношение  

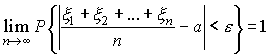
   Это непосредственно следует из формулы (54), так как  

   Замечание. Говорят, что случайная величина сходится по вероятности к числу А, если при сколь угодно малом вероятность неравенства с увеличением n неограниченно приближается к единице. Сходимость по вероятности не означает, что . Действительно, в последнем случае неравенство выполняется для всех достаточно больших значений n. В случае же сходимости по вероятности это неравенство для отдельных сколь угодно больших значений n может не выполняться. Однако невыполнение неравенства для больших значений n есть событие очень редкое (маловероятное). Принимая это во внимание, частный случай закона больших чисел Чебышева можно сформулировать так.    Средняя арифметическая попарно независимых случайных величин , имеющих ограниченные в совокупности дисперсии и одинаковые математические ожидания , сходится по вероятности к а.    Поясним смысл частного случая закона больших чисел Чебышева. Пусть требуется найти истинное значение а некоторой физической величины (например, размер некоторой детали). Для этого будем производить ряд независимых друг от друга измерений. Всякое измерение сопровождается некоторой погрешностью (см. подробнее § 6, п. 1). Поэтому каждый возможный результат измерения есть случайная величина (индекс i — номер измерения). Предположим, что в каждом измерении нет систематической ошибки, т. е. отклонения от истинного значения а измеряемой величины в ту и другую стороны равновероятны. В этом случае математические ожидания всех случайных величин одинаковы и равны измеряемой величине а, т. е.    Предположим, наконец, что измерения производятся с некоторой гарантированной точностью. Это значит, что для всех измерений . Таким образом, мы находимся в условиях закона больших чисел Чебышева, а потому, если число измерений достаточно велико, то с практической достоверностью можно утверждать, что каково бы ни было , средняя арифметическая результатов измерений отличается от истинного значения а меньше, чем на