1060963_B9CC3_zinenko_s_n_lineinaya_algebra

№ 11.4.

f1 = x0 ,

f2 = x1,

f3 = x2

1)

+1

g1 ≡

1

g1 = f1 ≡1

g1 = ∫

12 dx = 2

e1 =

−1

g1

2

2)

1

g2 = f2 −α2 1 e1 = x −α2 1

→

2

(

f2 , e1 ) =

1

+1

α1 =

2

∫ x dx = 0

−1

→ x −0 1 = x

+1

32

g2

23 x

g2 = ∫

x2 dx =

e2

=

=

2

−1

g2

3)

g3 = f3 −(α31 e1 +α3 2 e2 )= x2 −α31

1

−α3 2

3

x →

2

2

α31 =

(

f3, e1 )

= 12

+∫1 x2 dx = 3 22

−1

+1

(

f3, e2 )

=

3

3

dx = 0

α3 2 =

2

∫ x

−1

→x2 − 3 22 12 −0 23 x = x2 − 13 g3 =

+∫1 (x2 − 13 x )2 dx = 52

32 e3 = 52 23 (x2 − 13 )

Итак,

−1

1 (

)

e

=

1

, e

=

3

x, e =

5

3x

2

−

1

2

2

2

2

2

1

3

с весом ρ(x)

Замечание. Полиномы,

ортогональные на интервале

a,

b

называются

Лежандра

P (x)

−1, +1

1

n

1

ортогональными

Чебышева

Tn (x)

(−1, +1 )

многочленами

1 − x2

Лагерра

L n (x)

0, +∞

)

e

−x

Эрмита

H n (x)

(−∞, +∞ )

e−x2

№ 11.5.

Из формул Эйлера

e+i k x
	2		=
e−i k x
	2

1

2

1

2

U

U − 1=U *

// i

cos k x

cos k x

1

//

1

e+i k x

2

2

2

=

2

−i

sin k x

sin k x

1

−1

e−i k x

2

2 i

2 i

2

линейно связывающих экспоненту и тригонометрические функции, вытекает совпадение их линейных оболочек (пространство тригонометрических полиномов)

T2n+1 = Lin{... , sin k x, ... , 1, ..., cos k x, ...}= Lin{... , e −i k x , ... , 1, ... , e+i k x , ...} (k =1, ... , n)

В силу попарной ортогональности функций в смысле скалярного произведения

+π

(T, S )= ∫ T (x) S(x) dx

−π

после нормировки они образуют ортонормированные базисы в T2n+1 .

71

Проверим, что нормированные функции первой системы образуют ортонормированный базис

	{... ,	1	sin kx, ... ,	1	, ... ,	1	cos kx, ...}		( ek , el ) =	+π
										∫ ek
		π		2π		π
			\\	\\			\\			−π
			e−k	e 0			e+k
	Из 9	возможных ситуаций, очевидно, различными являются 6:								k

Рассмотрим сначала “диагональные” случаи:

?

(x) el (x)dx =δk l

l

(+,+) (+,0) (+,−)

(0,+) (0,0) (0,−)

(−,+) (−,0) (−,−)

+π

k =l

1+π

(

k

)2

1

+π1

+cos2k x

dx

(+, +): (ek , el )= π1

π

∫

cos kx

dx = π

∫

2

∫

+−ππ

−π

cos k x cosl xdx =

1

−π

∫

(cos(k

−l )x + cos(k + l )x)dx

k ≠l

2π

(0,0):

( e0 , e0 )=

1

+∫π

−π

1 dx =1

2π

+π

+π

−π

−cos22

k x dx

1

+π

k =l

π1

∫

(sin k x)2 dx = π1

∫ 1

(−, −):

∫

−π

−π

(ek , el )= π

sin k x sin l x dx =

1

+π

(cos(k

−l )x − cos(k + l )x)dx

−π

∫

k≠l

2π

−π

Теперь рассмотрим “верхне-треугольные” случаи

=21π 2π =1

=0

=21π 2π =1

=0

(+,0): ( ek , e0 )

=

1

+∫π cos kxk dx = 0,

(0, −): ( e0 , el )= −

1

+∫π sin l x dx = 0

2π

2π

−π

−π

(+, −): (ek , el )= −

1

+∫π cos k x sin l x dx =

1

+∫π (sin (k −l )x − sin (k + l )x)dx = 0

π

2π

−π

−π

Замечание. Переобозначив коэффициенты тригонометрического полинома

T =T (x) = 12 a 0

n

+ ∑(ak cos kx + bk sin kx)= ... + bk sin kx + ... + 12 a0 + ... + ak cos kx + ... =

k =1

n

= ... +

π bk

π sin kx + ... +

2 a0

2π

+ ... +

π ak

π

cos kx + ...

=

∑ dk ek

1

π

1

1

\\

\\

\\

\\

\\

\\

k =−n

d−k

e−k

d0

e0

d+k

e+k

{ek },

получим

разложение

вектора

T

по

ортонормированному

базису

так что

координаты dk

равны

+π

ak

=

1

dk

= π1 ∫ T (x) cos k x dx,

k = +1, ... , +n

π

+π

−π

+π

dk = (T, ek )=

∫

T (x)

ek (x)

dx

a0

=

π2 d 0 = π1 ∫ T (x) dx,

k = 0

−π

−π

1

+π

bk

=

d−k = π1 ∫ T (x) sin k x dx,

k = +1, ... , +n

π

Замечание. Проверка ортогональности функций {ek

−π

k = 0, ±1, ... , ± n } еще проще

= ei k x ,

+π

+π

+π

k =l

+∫π 1 dx = 2π \\

( ek , el )= ∫ ek (x) el (x)dx = ∫ e

i kx

e

−i lx

dx = ∫ e

i

(k −l )x

−π

2π δk l

dx =

e i (k −l )x

+π

−π

−π

−π

//

k≠l

i (k −l )

=

0

−π

72

Дополнение.

Пусть y = y ( x) - функция (вектор-функция векторного аргумента), отображающая

x

y

y ( x)

//

//

//

x1

y1

y1(x1,

... , xj , ... , xn )

Rn X

y

Y Rm

...

...

yi (x1,

...

→

xj

→

yi

=

... , xj , ... , xn )

...

...

...

ym (x1,

xn

ym

... , xj , ... , xn )

В частности,

если функция y линейна (линейный оператор)

y (α1 x1 + α2 x 2 ) =α1 y ( x1) + α2 y ( x 2 )

то ее естественной областью

определения

является все

пространство X ≡ Rn ,

действие сводится к умножению

матрицы

A на вектор-столбец

x :

y = A x ,

а областью

значений

является

некоторое

подпространство

Y = Ran A Rm .

Функция y = y ( x)

дифференцируема

в

точке

x , если

ее

приращение

допускает

выделение линейной главной части

d x

//

∆y( x) = y ( x + ∆x ) − y ( x) = D( x) ∆x + o( || ∆x || )

\\

называемой дифференциалом функции.

d y( x)

Найдем компоненты матрицы-функции

(Якоби)

D( x) =

:

di j

=( ei ,

D( x) e j ).

di j

Выбирая приращение аргумента

∆ x =e∆t

вдоль некоторого единичного направления

e (

e

=1) , приходим к производной вектор-функции y в точке x по направлению e

y'e ( x) =

lim

∆e y( x)

=

lim

D( x) e ∆t + o(∆t )

= D( x) e

∆t

∆t

∆ t→0

∆ t→0

В частности, взяв один из векторов ортонормированного базиса {... , ej , ...}

e =e j ,

получим вектор частной производной вектор-функции

y ( ... , xj ,

... )

по переменной x j

y'

( x) =

lim

y ( ... , xj

+ ∆xj ,

... ) − y (

... , xj ,

... )

= D( x) e

j

x j

∆x j →0

∆x j

Отсюда вытекает, что элементами матрицы Якоби D являются частные производные

di j	= ( ei , D e j )= ( ei , yy'	)= yi′′
	x j	x j
компонент yi ( ... , xj , ... )	вектор-функции y ( x) по переменным xj . Поэтому матрица

Якоби называется еще матрицей-производной вектор-функции y ( x) и обозначается

y′1′x

... y′1′xj

... y′1′x

'

1

j

n

y′′

... y′′

...

y′′

D( x) =Y x ( x)

=

ii x

ii xj

j

ii x

1

n

y′′

... y′′

... y′′

Тогда,

mx1

mx j

mxn

d y =Y

'

d x

y'

=Y

'

e

y '

=Y

'

e j

y′′

= ( ei , Y

'

e j )

x

e

x

y x

j

x

i

x j

x

73

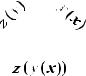
Пусть, далее, z = z ( y), y = y ( x) две функции, отображающие соответственно

y	z		Y
Rn X → Y	→ Z Rm
∩|		Z	←	X
Rl
так что можно построить сложную функцию z = z ( y ( x)) .
Из дифференцируемости каждой функции
∆z = z ( y + ∆y ) − z ( y) = Z 'y ∆y + o( || ∆y || )
∆ y = y ( x + ∆x ) − y ( x) = Y 'x ∆x + o( || ∆x || )
вытекает дифференцируемость сложной
∆z = z ( y ( x + ∆x) ) −z ( y ( x)) = z ( y + ∆y ) − z ( y) = Z 'y ∆y + o( || ∆y || ) =
= Z 'y ( Y 'x ∆x + o( || ∆x || )	+ o( || ∆x || ) = Z 'y Y 'x ∆x + o( || ∆x || )
откуда следует	//
	Z 'x = Z 'y Y 'x

Из покомпонентной записи полученного матричного равенства получаем формулы для частных производных сложной функции нескольких переменных

zi′	= zi′		y1′	+ ... + zi′	yk′	+ ... + zi′	yl′	l		yk′
								= ∑ zi′
x j	y1		x j	yk	x j	yl	x j	k =1	\ yk	x j
Сравнить. Если z =B y ,			y =A x - линейные операторы, задаваемые матрицами B , A , то

сложнаяфункция z = B(Ax) такжелинейнаизадаетсяпроизведениемматриц: z =(B A)x .

В случае квадратных матриц-производных

m =l =n

можно

говорить об их

определителях (якобианах), которые,

очевидно,

связаны равенством

D(z1, ... , z i ,

... , z n )

=det Z

'

= det Z ' det Y

'

=

D(z1, ... ,

z i , ... , z n )

D( y1, ... , yk , ... , yn )

D(x1 , ... , xj , ... , xn )

D( y1 , ... , yk , ... , yn )

D(x1 , ... , xj , ... , xn )

x

y

x

Наконец, если

y = y ( x),

z = z ( y) = x

x = x( y)

две взаимно обратные функции

Rn X

y

x = x ( y ( x)),

x X

←→ Y Rn :

y Y

то

x

y = y ( x ( y)),

X 'x = X 'y Y 'x

(

X '

=Y ' = I

)

X ' =Y '

−1

'

'

'

x

y

y

x

Y y =Y x

X y

так что матрицы Якоби Y 'x и X 'y взаимно обратные. Следовательно, их якобианы связаны соотношением

D( y

1

, ... , y

i

, ... , y

n

)

= det Y 'x = (det X 'y )

−1

=

(

D(x1, ... , xj ,

... , xn )

)

−1

D(x1 , ... , xj , ... , xn )

D( y1, ... , yi ,

... , yn )

74

12.СОБСТВЕННЫЕ ВЕКТОРЫ И СОБСТВЕННЫЕ ЗНАЧЕНИЯ САМОСОПРЯЖЕННОГО И УНИТАРНОГО ОПЕРАТОРА

№12.1.

Дана матрица A (V ).

-проверить самосопряженность матрицы A (унитарность V )

-показать, что оператор A , задаваемый матрицей A в евклидовом пространстве Cn ,

	самосопряжен
	(оператор V , задаваемый матрицей V в евклидовом пространстве
-	найти собственные векторы {tk } и собственные значения { λk }
-					= λ
	проверить, что собственные значения вещественны λ
			= λ −1 )
	(по модулю равны единице λ

Cn , унитарен) оператора

-проверить, что собственные векторы, отвечающие различным собственным

значениям λi ≠ λ j , ортогональны t i t j

-найти ортонормированный базис из собственных векторов { uk }

-построить матрицу перехода U к этому базису и проверить, что она унитарна

-проверить справедливость разложения

A =U Λ U* (V =U Λ U*)

		1	−3	6				−3	3	−2
a. A =						a. A =
		−3	1	6			± 3		−1 −2 3
		6	6	2				−2	−2 3	0
		1	−3	6				−3	3	−2
b. V = 14						b. V = 14
		−3	1	6			± 3		−1 −2 3
		6	6	2				−2	−2 3	0

№ 12.2.

Показать, что в евклидовом					пространстве T2n +1	тригонометрических			полиномов
( № 11.5. ) дифференциальный (интегральный) оператор самосопряжен.
Найти ортонормированный базис из собственных векторов.
1			d		+π		i k ( x−t)	T (t)dt, (k = 0,	±1, ... , ± n)
					J k T = ∫	e
DT =	i		dx	T (x)
					−π

75

Теория

Оператор называется

- A* - сопряженным к оператору A , если

( A* a, b )= ( a, Ab ), a, b En

- A - самосопряженным, если

( Aa, b )= ( a, Ab ),			a, b En		A* = A
- U - унитарным, если
( Ua, Ub )= ( a, b ),			a, b En	U U* = U* U = I	U* = U − 1
Собственные значения самосопряженного оператора вещественны
A f = λ f							= λ ,
					λ
а унитарного по модулю равны единице
U f = λ f			=1
	λ λ				λ = λ −1

Собственные векторы, отвечающие различным собственным значениям - оpтогональны.

A f = λ f	,	U f = λ f	,	λ ≠ µ	f g ( f , g)= 0
A g = µ g		U g = µ g

Замечание. Сопряженные, самосопряженные и унитарные операторы во множестве

линейных операторов в комплексном пространстве				En	играют	роль сопряженных,
вещественных и единичных по модулю комплексных чисел: z ,					z = z,	z = z −1.
Теорема (спектральная теорема)
	Всякий самосопряженный	A* = A	(унитарный	U* = U − 1 )		оператор обладает
	ортонормированным базисом из собственных векторов
	A f k = λk	f k	( fi , f j )=δi j i,		j =1,..., n

Аналогичные понятия вводятся для матриц.

Пусть A - матрица некоторого оператора A в некотором ортонормированном базисе {e }

{e }

a

(

Ae

, e

i )

A → A = a

i j

=

i j

j

Тогда сопряженному оператору A* соответствует матрица

{e }

A* → A* = a*

a*

=

(

A*e

,

e

i )

=

(

e

, Ae

i )

=

(

Ae

, e

j )

= a

j i

i j

i j

j

j

i

получившая название сопряженной к A матрицы. В таком случае: - самосопряженная матрица

A* = A ai j = a j i

- унитарная матрица

U U * =U * U = I U * =U − 1

Замечание. Столбцы унитарной матрицы составляют некоторый ортонормированный базис в Cn

Замечание. В отличие от операторов, определения для матриц вводятся без всякой связи с каким-либо скалярным произведением, а как свойства их компонент. В то же время в евклидовом пространстве Cn с каноническим скалярным произведение ( № 11.1. a. )

n

( x, y )= ∑xk yk

k =1

эти матрицы порождают соответствующие операторы

( Ax, y )= ( x, A* y ); ( Ax, y )= ( x, Ay ); (U x, U y )= ( x, y ) x, y Cn

76

В вещественном случае матрицы: - сопряженная

A* ≡ A′ a*i j = a j i - это просто транспонированная матрица

- самосопряженная

A = A′ ai j = a j i - симметричная матрица

- унитарная

U U′ =U′ U = I U′ =U −1 - ортогональная матрица

Пусть

{λ1, ... , λk , ... , λm }

все различные собственные значения самосопряженного A (унитарного V ) оператора, соответствующие собственным подпространствам

{F1, ... , Fk , ... , Fm }

Обозначим ортонормированные базисы собственных подпространств через

{{

f1

1

, ... , f1

n1

}, ... , {

fk

1

, ... , fk

nk

}, ... , {

fm

1

, ... , fm

n m

}}

Объединенная система подбазисов образует не просто ортонормированную систему, а, как следует из спектральной теоремы для самосопряженных (унитарных) операторов,

ортонормированный базис { f } из собственных векторов в евклидовом пространстве E .

Следовательно, самосопряженный оператор A (унитарный оператор V ), имеющий в

некотором (старом) базисе

{e }

самосопряженную матрицу A (унитарную матрицу V ),

в новом ортонормированном базисе (новом)

{

f }

из

собственных

векторов имеет

диагональную матрицу

λ1

0

0

0

λ1In1

0

0

0

λ1

λk

0

I

Λ =

0

0

=

0

λ

k

n k

0

0

λk

λm

0

0

0

0

0

0

λm

λm In m

(любой самосопряженный или унитарный операторы – диагонализируемы).

Обозначим через uk i

столбец-координат собственного вектора

fki , соответствующим

собственному значению λk , в старом базисе { e }. Тогда матрица перехода от старого

ортонормированного базиса

{e }

к новому

ортонормированному

{ f } базису из

собственных векторов является унитарной

U = u

11

,

... , u

, ... , u

k 1

,

... ,u

k n k

, ... , u

m1

,

... , u

1 n1

m n m

Следовательно, имеет место спектральное разложение самосопряженной (унитарной) матрицы

A =U Λ U − 1 =U Λ U * (V =U Λ U *)

77

№ 12.1. a.		1	−3 ±	6
	A =	−3	1	6
		6	6	2

-Проверка самосопряженности вещественной матрицы A - это просто проверка симметричности матрицы, т.е. проверка равенства элементов матрицы, стоящих на симметричных местах относительно главной диагонали.

-Покажем, что оператор A , задаваемый матрицей A в евклидовом пространстве Cn , самосопряжен. Действие линейного оператора A полностью определяется его действием на базисные векторы Ae j , т.е. самосопряженность достаточно проверить на базисных векторах

( Ae j , ei )= ai j = a j i = a j i = ( Aei , e j )= (e j , Aei )

-Найдемсобственныезначения λk и собственныевекторы tk оператора.

pA (λ) =det (A−λI )=	1−λ −3		6	=−λ3 +4λ2 +16λ−64=−(λ−4)2 (λ+4) λ1 =4, λ2 =−4
	−3	1−λ	6
	6	6	2−λ

(Отметим, что собственные значения вещественны λ = λ ). Далее

(A −λI )t = 0

λ1	?
	t1
	1 − 4 −3		6			x				0
	−3 1 − 4 6					x1		=		0
	6					2
		6 2 − 4				x				0
						3
λ2	?
	t2
	1 + 4 −3		6			x				0
	−3 1 + 4 6					x1		=		0
	6					2
		6 2 + 4				x				0
						3

	xx1						−11
			= x		1				+	1 x			60
	2									3	2
	x						±0						3
	3
							\\						\\
							t11						t1 2
	x						−		6
	x1		=	1 x			−		6
	2			2		3
	x								2
	3

\\

t 2 1

-Проверим, что собственные векторы, отвечающие различным собственным значениям λ1 ≠ λ2 , ортогональны t1 t2 ;

							−1		− 6									6 − 6
		(t11 , t 2 1 )= (					1	,	− 6 )	= 0,		( t1 2 , t 2 1 )= (						0 ,			− 6 )= 0
							0		2									3							2				{u1, u2 , ...},
-		Найдем			ортонормированный						базис из						собственных						векторов
1)		ортогонализируя найденный базис из собственных векторов {{ t11																								, t1 2 }, {t 2 1 }}
					−1																g11							−1					−2 2
g		= t		=	1						g					= 2	u		=						=	1		1		=	1		2 2
	11		11									11						11
					0																g					2		0			4		±0
																						11

78

2)											−2 2																															66
g1	2	=t1	2	−α1 u1	1	=	60	−α1	1		2 2				= → α1 =							( t1	2	, u1		1	) = 3							→				1
									4		0																											2				6
							3
																													g1 2													6						2
													g							=2 3				u			=							=		1						6			=1			2
														1											1 2
															2														g						4 3							6			4		2	3
3)																														1 2
																																							−			6
g 2 1 =t 2 1 −(β1 u11 +β2 u1 2 )= →											(t 2 1 {u11 , u1 2 })
																						→ β1 =β2 =0												→ = −								6
																																										2
																																									g					−		6
													g	2							=4													u		2		=				2 1		=1		−		6
															1																						1				g				4
																																										2 1						2

-Построим матрицу перехода U к этому базису

								−2		2	2 − 6
U = u	11	, u	1 2	, u	2 1		= 1		2 2		2 − 6
							4			±0		2
											±2 3

Очевидно матрица U унитарная (ортогональная), что является следствием ортонормированности базиса

U U′ =U′ U = I U′ =U −1

-Проверку справедливости разложения

			1 −3 6										−2 2					2 −			6		+4 0 0											−2 2 2 2								0
A =			−3				1 6			= 1				2 2				2 −			6					0 +4 0									2			2 2 3							1 =U	Λ U′
											4																																		4
			6 6					2							0 2 3											0 0 −4									− 6		− 6
																					2																					2
удобно провести в следующем виде
																			A U =U Λ
																	λ1		0			0
A u		11	, u	1	2	, u	2	=	u		11	, u		1 2	, u	2 1		0 λ		1		0					Au	11	, Au			1 2			, Au			=		λ u				,λ u		,λ	2	u	2 1
								1																												2 1					1 11				1 1 2
																		0	0
																					λ2
№ 12.1. b.																			1		−3					6
															V = 14			−3				1				6
																			6			6				2
-	Проверка							унитарности							(ортогональности)											матрицы					V = v					1	, v	2	,	v	3				равносильна

проверке, образуют ли столбцы {v 1, v 2 , v 3 } матрицы ортонормированный базис в Cn .

Замечание. Нетрудно видеть, что V к тому же самосопряженная (симметричная) матрица, так что собственные значения ожидаются вещественными и единичными по модулю: λ = ±1.

79

Покажем, что оператор V , задаваемый																		матрицей V в евклидовом пространстве			Cn ,
унитарен. Действие линейного оператора																		V полностью определяется его действием на
базисные векторы V e j =v j								и представляют собой столбцы матрицы V (которые образуют
ортонормированный базис):
							(V ei , V e j )= (v i , v j )=δi j = (ei , e j )
-	Найдем собственные значения λk и собственные векторы tk оператора.
			1 −λ						−	3			6
		±
													4
			4		3			4										=−λ3+λ2 +λ−1=−(λ −1)2 (λ +1) λ
p	(λ) =det (V −λI )=			−				± 1 −λ					6						=1, λ	2	=−1
													4
V			4					4										1
				6					6					2	−λ
			4					4					4

(Отметим, что собственные значения единичны по модулю λ = λ−1 ). Далее

(V −λI )t = 0

λ1		?
			t1
	1		−1			−	3						6			x1		0
										4
4			3			4
−					± 1 −1								6			x		= 0
		64				4 6				4							2		0
																	x
										±		2	−1				3
	4					4
										4
λ2		?
			t2

x1

x2x3

			−1			+ 1 x	±	6
	= x			1				0
		2		±0		3 3		3
				\\				\\
				t11				t1 2

	1								3				6
4 +1							−										x1			0				x1						− 6
									4				4
	−		3		± 1				+1				6					x		=	0			x				= 1 x		−	6
													4
	46						4		6									x			0				x			2	3		2
																		2							2
											±		2	+1		3								3
	4						4						4
																														\\
Замечание.																														t 2 1
											Полученные									собственные				векторы					совпадают векторами							предыдущего
№ 12.1. a. , так что
								1 −3 6											−2 2				2 −	6			+1 0 0							−2 2 2 2		0
V =1							−3			1 6							=1			2 2			2 −	6				0 +1 0						2	2 2 3		1	=U Λ U′
	4																	4																			4
							6			6			2							0 2 3														− 6 − 6
																								2				0 0 −1								2

№ 12.2.

Интегрируя по частям, “перенесем” дифференцирование с первого сомножителя на второй

+π

+π

+π

+π

(DT, S)=

1

d

T (x)

dx =1

T (x)

−

T (x)

d

dx =

T (x)

1

d

S(x)

dx =(T, DS )

S(x)

S(x)

S(x)

∫

i dx

i

(

−π

∫

dx

)

∫

i dx

−π

\\

−π

−π

0

и тем самым найдем вид сопряженного оператора D*, откуда вытекает D* = D .

Рассмотренный в № 11.5. ортонормированный базис e

k

=

1

ei k x , как нетрудно видеть, и

2π

есть базис из собственных векторов, отвечающих собственным значениям λk = k :

1 d

1

i k x

1

1

i k x

1

i k x

= k ek (k = 0, ± 1, ... , ± n)

Dek =

e

=

ik

e

= k

. 2π

e

i

dx

2π

i

2π

80