1060963_B9CC3_zinenko_s_n_lineinaya_algebra

13. ОРТОПРОЕКТОРЫ. СПЕКТРАЛЬНОЕ РАЗЛОЖЕНИЕ САМОСОПРЯЖЕННОГО И УНИТАРНОГО ОПЕРАТОРА.

№ 13.1.

Дано подпространство S V (плоскость в пространстве)

-

найти ортонормированные базисы

{ i ,

j } ,

{ k }

в подпространстве

S V и его

ортогональном дополнении L =V S

P,

Q

-

матрицы

P,

Q;

P , Q операторов

ортогонального

проектирования

(ортопроекторов) на подпространства S, L

в старом базисе { i ,

j,

k } и новом

базисе{i ,

j,

k }

-

проверить, что

P*

I = P +Q,

P2 = P

,

= P

P Q = Q P

= 0

2

= Q

Q*

= Q

Q

- найти ортогональные проекции f S ,		g L произвольного вектора
	h = xi + y j + z k V
x − y + 2 z = 0		6x + 6 y + 2 z = 0
№ 13.2.
Для самосопряженного	A (унитарногоV ) оператора, заданного		в	евклидовом
пространстве Cn с	каноническим	скалярным произведение	(	№11.1. a. )

самосопряженной A (унитарной V ) матрицей в № 12.1. a. ( № 12.1. b. )

-найти ортопроекторы Pk на собственные подпространства Fk и проверить их

свойства

P * = P ,		P	j	P = P P	j	=δ	i j	P	j
k	k			i i

-проверить ортогональное разложение единицы

I = ∑ Pk

k

-и спектральное разложение самосопряженного (унитарного) оператора

A = ∑ λk Pk

k

			1	−3	6					−3	3	−2
a. A =							a. A =
			−3	1	6				± 3		−1−2 3
			6	6	2					−2	−2 3	0
			1	−3	6					−3	3	−2
b. V =	1						b. V =	1
	4		−3	1	6			4	± 3		−1−2 3
			6	6	2					−2	−2 3	0

№ 13.3.

Построить спектральное разложение самосопряженного оператора ( № 12.2. )

			d		+π	i k ( x−t)		(k = 0, ±1, ... , ± n)
1					JkT = ∫ e		T (t)dt,
DT =				T (x)
	i		dx
					−π

81

Теория

Пусть {e } некоторый произвольный ортонормированный базис в евклидовом пространстве E . Разобьем его на две ортонормированные (в частности, линейно независимые) подсистемы

{e } ={{ f1, ... , fm }, { g1, ... , gn−m }} ={ f } { g }

и построим подпространства (линейные оболочки)

F = Lin{ f1, ... , fm }, G = Lin{ g1, ... , gn−m } F G

Тем самым, получим разбиение всего пространства в ортогональную сумму E =F G .

Замечание. Ортогональное дополнение G F в отличие от “косого” – единственное, поэтому для него корректно введение соответствующего обозначения (ортогональная разность)

G = E F

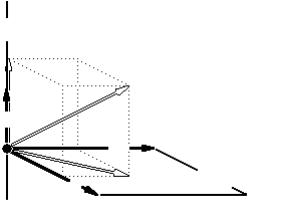
Далее, разлагая произвольный вектор h E

h = (α1 f1 +...+αm fm ) + (β1g1 +...+βn−m gn−m ) = f + g

\\	\\
f	g

G = L

E =V = L S

g

h
g1
f2
f	F = S
f1

получим его разложение (однозначное) на ортогональные составляющие F f g G , получившие названия ортопроекций вектора h на подпространства F и G (уточнять, параллельно какому подпространству в силу его единственности – излишне).

Тем самым определяются ортопроекторы						P,		Q на подпространства F и G = E F
		P	=Ph,					Q
	h→ f							h→g =Qh
Очевидно,
			P	2	=P			*
I =P +Q,							,	P = P		P Q =Q P =0
		Q2 =Q						Q* = Q
при этом
F = Ran P,	G = Ker P;							G = Ran Q,			F = Ker Q
Нетрудно видеть, что	матрицы			P ,			Q	операторов		проектирования P, Q в
“естественном” ортонормированном базисе								{ e } ={ f } {		g }	равны
		Im	0						0 0
	P =	0 0				,		Q =	0 In−m

В матричном представлении свойства операторов проектирования - очевидны.

82

№ 13.1.

Плоскость S задана как множество решений “однородной системы”, состоящей из одного уравнения с тремя неизвестными

									1 x −1 y + 2 z = 0
Решая данную систему, найдем базис { p,																	q }	в S (сначала какой-нибудь). Имеем
																		x		2z					±1									−		2
																			1y −											+ z
x − y + 2z = 0					x =1y −				2z									y	= 1y			= y					1									0
																		z		1z							0								±1
																											\\							\\
Ортогонализируем полученный в S базис:																											p								q
1)
	1																								p									1						2
p = p =	1									p						= 2				f		=					=			1				1		=		1		2
																					1				p					2								2
	0																																	0						0
2)
			− 2				2																				− 2
q = q −α f1	=		0		−α 1		2		= → α = ( q, f1 )= +1 →															1						2
			1		2		0																	2						2
																								q									−	2						−1
										q					= 2					f2		=					=	1									=		1
																																		2						1
																								q				2		2									2
																																		2
																																								2

Далее. Каждое уравнение системы в свою очередь можно рассматривать, как скалярное произведение некоторого фиксированного вектора с радиус-вектором точки

	1			x		( n, h )=1 x −1 y + 2 z = 0
n =	−1		,	h =	y
	2
					z

Тем самым, автоматически задается ортогональное дополнение L =V S , как линейная оболочка векторов, составленных из коэффициентов уравнений системы. В данном случае L = Lin{n } - это одномерное подпространство (прямая с направляющим вектором n ).

Нормируя вектор n , получим “ортонормированный” базис в L :

n

1

n

= 2 g

=

= 1

−1

1

n

2

2

Замечание. Переход к новому ортонормированному базису { f1, f2 , g1 } = {i , j, k } пространства V означает выбор новой системы координат { Oxyz }, в которой плоскость

S становится координатной плоскостью { x O y }	и имеет простейшее уравнение z =0 .
Роль ортогонального дополнения L =V S	играет ось { O z } . Нахождение

ортогональных проекций радиус-вектора точки в новой системе координат тривиально

x

S f

x

1 0

0 x

0

0 0 0 x

h = y

= y =

0

1

0

y

= Ph,

L g = 0 =

0 0

0

y

= Qh

0

0

0

0 0

1

z

0

z

z

z

\\

\\

P

Q

83

Посмотрим, как найти проекции	в старом базисе {i , j, k }.	Построим	унитарную
матрицу перехода от старого ортонормированного базиса		{i , j, k }	к новому
ортонормированному базису {i , j,	k }

2

−1

1

U =

i , j , k =

1

2

1

−1

2

±0±

2 ±

2

Ортопроекторы P,

Q на ортогональные подпространства

S,

L

2 −1 *

1 0 0

2 2 ±0

2 −1

2 2

0 1 0

−1 1 2

12

2 1

P =12

2 1 ±*

=14

−1 1

±0 2 *

0 0 0

* * *

±0 2

\\

задаются матрицами

0						3	1 −	2
		=	1
2			4		−	1	3	2
						2	2	±2

									P
			* *									* *		*														1	−1 2
				1				0	0 0				±							1
	1															1		1								1
Q =	2		* *	−1				0	0 0			±* * *				2	=	4		−1			1 −1 2		=	4		−1	1 − 2
			* *	2			0		0 1			1 −1 2								2							2 −		2 ±2
									\\
									Q

Проекции произвольного вектора			x
		h = xi + yj + zk = y
			z
на подпространства S, L	равны

V

3 1−

2

x

3x +

y − 2z

1

1 3

2

y

1

x +

3y + 2z

=

f = Ph = 4

= 4

− 2 2

2 y + 2z

2 z

− 2x +

= 14 (3x + y − 2z)i + 14 (x + 3y + 2z) j + 14 (− 2x + 2 y + 2z)k S

1 −1

2

x

x −

y + 2z

1

g = Qh = 1

−1

1 −

2

y

= 1

−x +

y − 2z

= 1 (x − y +

2z)

−1

= (h, k )k

=

4

4

4

2 − 2

2

z

2x −

2 y + 2z

2

= 14 (x − y + 2z)i − 14 (x − y + 2z) j + 14 2 (x − y + 2z)k L

Замечание. Новый ортонормированный базис { i , j, k }

имеет ту же ориентацию, что и

исходный старый базис {i ,

j,

k },

в чем можно убедиться, выяснив знак смешанного

произведения

( i , j, k )= det i ,

1

2

−1

1

j,

k

= detU =

2

1

−1

=1 > 0

23

0

2

2

т.е. новый базис получается из старого поворотом в пространстве. В этом состоит геометрический смысл ортогональных матриц, описывающих поворот на некоторый пространственный угол, если detU =1 > 0 (если detU = −1 < 0 , то осуществляется поворот с зеркальным отражением относительно какой-либо оси).

84

№ 13.2.

Пусть

{λ1, ... , λk , ... , λm }

все различные собственные значения самосопряженного A (унитарного V ) оператора, соответствующие собственным подпространствам

{F1, ... , Fk , ... , Fm }

Обозначим ортонормированные базисы собственных подпространств через

{{

f1

1

, ... , f1

n1

}, ... , {

fk

1

, ... , fk

nk

}, ... , {

fm

1

, ... , fm

n m

}}

Из спектральной теоремы для самосопряженных (унитарных) операторов вытекает, что объединенная система подбазисов образует в целом ортонормированный базис { f } из собственных векторов в евклидовом пространстве E .

Далее, произвольный вектор пространства может быть однозначно разложен по базису

h = (x11 f11 +... +x1n1 f1n1 )+... + (xk1 fk1 +... + xknk fk nk )+... + (xm1 fm1 +... + xm n m fm n m )
\\	\\	\\
f1 F1	fk Fk	fm Fm
т. е., в данном случае, в ортогональную сумму собственных векторов		fk
h = f1 + ... + fk + ... + fm	E = F1 ... Fk ... Fm

получивших название ортогональных проекций вектора h на собственные подпространства Fk .

Действие оператора A сводится к умножению каждого слагаемого на соответствующее собственное значение

A h = λ1 f1 + ... + λk fk + ... + λm fm

Определим операторы ортогонального проектирования (ортопроекторы)

Pk

= P h

P* = P ,

P

P = P P

= δ

P

h→ f

k

j

j

i j

j

k

k

k

i

i

Полученным выше разложениям произвольного вектора h

и действию оператора

A с

помощью ортопроекторов можно придать вид:

E =F1 ... Fk ... Fm

h

=

f1 +... + fk +... + fm

I = P1 +... +

Pk +...+ Pm

...

...

...

...

A

=λ

k

I

n

=λ

+

+λ

+

+λ

m fm

=λ

1P1

+

+λ

k Pk

+

+λ

mPm

Ah

1 f1

k fk

A

Fk

k

Замечание. Самосопряженный (унитарный) оператор являются частными случаями диагонализируемого оператора, с уточнением, что базис из собственных векторов можно выбрать ортонормированным, а собственные значения вещественны (единичны по модулю).

85

Самосопряженный A (унитарный V ) оператор, задаваемый в евклидовом пространстве Cn с каноническим скалярным произведением самосопряженной A (унитарной V ) матрицей, как показано в № 12.1. a. (№ 12.1. b. ), имеет собственные подпространства

	−2 2						2						−		6
F1 = Lin{u11 , u1 2		2 2		,			2		},	F2	= Lin{u2 1	}={14		−	6	}
	}={14				14	±2
		0					3								2

соответствующие собственным значениям λ1 =4, λ2 =−4 ( µ1 =1, µ2 =−1).

Построим унитарную матрицу перехода от старого канонического ортонормированного

базиса {e1,			e2 , e3 } к новому ортонормированному базису																																		{u11 , u1 2 , u2 1 }={e1, e2 ,									e3 }
																													−2 2								2		−	6
												U =						,							1					2 2							2		− 6
																	e1, e2		e3 =						4
																														±0 ±2							3			2
Ортопроекторы P1,					P2		на ортогональные подпространства F1, F2																																	задаются матрицами
		−2 2				2																									10 −6 2 6
P =	1		2 2		2					−2 2 2 2								0		1	=			1							−6						10 2 6
																						16
1	4			0	2 3											2 2 2 3				4										2 6 2 6 ±12
					− 6														1											6							6 −2 6
P2 =				1																				1
					− 6					−						6	− 6 2				=									6							6 −2 6
				4																4			16
						2																																		±4
																												−2 6 −2 6
Непосредственно проверяется ортогональное разложения единицы
			1 0 0							1							10 −6 2 6													1							6			6−2 6
I =				0 1 0				=									−6 10 2 6											+									6			6−2 6			= P1 + P2
													16																				16
																2 6 2 6 12																				−2 6−2 6					4
				0 0 1
и спектральное разложение самосопряженного оператора, задаваемого матрицей A (V )
		1 −3 6															10 −6 2 6																				6			6−2 6
A =	−3 1 6						= 4					1					−6 10 2 6											−		4		1					6			6−2 6			= λ P		+	λ	2	P		2
		6 6			2					16							2 6 2 6 12													16											4			1 1
																																				−2 6−2 6
		1 −3 6															10 −6 2 6																				6			6−2 6
V = 1	−3 1 6						= 1				1						−6 10 2 6											−		1	1						6			6−2 6			= µ	P	+	µ	2		P		2
4	6 6				2					16							2 6 2 6 12													16											4			1 1
																																				−2 6−2 6

Замечание. Для того, чтобы вещественные матрицы имели вещественное спектральное разложение, очевидно необходимо, чтобы корни их характеристических полиномов были

вещественны. Для симметричных матриц A′ = A это выполнено всегда. В то же время

ортогональные матрицы U′ =U −1 имеют вещественное разложение, если корни их характеристических полиномов (всегда единичные по модулю) равны ±1. Это выполнено, если ортогональная матрица одновременно симметрична.

Вчастности, характеристические полиномы ортогональных матриц 2 го порядка, описывающих повороты плоскости, могут не иметь вещественных корней (соответственно нет собственных векторов). Геометрически это почти очевидно: после поворота вектор останется коллинеарным самому себе только при углах кратных π .

Вто же время при поворотах пространства, описываемых ортогональными матрицами 3 го порядка, имеется хотя бы одна неподвижная ось (собственное подпространство),

поскольку полиномы 3 го порядка обязаны иметь хотя бы один вещественный корень (?!).

86

№ 13.3.

Пусть {e } некоторый произвольный ортонормированный базис в евклидовом

пространстве E

{e } ={ e1, ... , ek , ... , en }

Построив линейные оболочки

Fk = Lin{ ek } Fi Fj

получим разбиение всего пространства в ортогональную сумму одномерных подпространств

E = F1 ... Fk ... Fn

(аналог трех осей координат Ox, Oy, Oz		в геометрическом пространстве	V с
ортонормированным базисом {i , j,	k }).		{ e }
Разложим произвольный вектор	h E	по ортонормированному базису
(конечномерный аналог ряда Фурье)

h = x1e1 + ... + xk ek + ... + xnen

Координаты xk (коэффициенты Фурье) в ортонормированном базисе равны

xk = ( h, ek )

Тем самым, получим вид ортогональных проекций вектора h и, соответственно, одномерных операторов проектирования на “координатные оси” Fk

Pk	= xk ek = ek ( h, ek ) Pk h = ek ( h, ek )
h→ fk

Замечание. Имеет место аналог теоремы Пифагора, получивший название равенства Парсеваля

n

n

h

2 = ∑

xk

2 =

∑( h, ek

)2

k =1

k =1

Самосопряженный дифференциальный оператор ( № 12.2. )

DT =

1

d

T (x)

i dx

в евклидовом пространстве T2n+1 тригонометрических полиномов имеет простой спектр

λk

= k

(k = 0, ±1, ... , ± n)

и, соответственно, одномерные собственные подпространства

Fk = Lin{ek } = Lin{

1

ei k x }

2π

Следовательно, операторы проектирования задаются формулами

(T, e

)=

1

ei k x +π T (t)

1

dt =

1

+π ei k x e−i k t T (t)dt =

1

1

P T =e

ei k t

J

T P =

J

k

k

2π

2π

k

2π

k

k

∫

2π

2π

∫

k

−π

−π

Тем самым, приходим к спектральному разложению самосопряженного оператора

1

n

1

d

1

n

+π

D = ∑λk Pk

=

∑ k Jk

T (x) =

∑ k ∫ ei k ( x−t) T (t)dt

π

π

k

2

k =−n

i dx

2

k =−n

−π

87

14. КВАДРАТИЧНЫЕ ФОРМЫ

№ 14.1.	Найти ортогональное преобразование										x =U x ,							приводящее						квадратичную
форму K ( x ) = (			A x, x )		к каноническому виду (						Λ x, x )					( № 12.1.,							№ 13.2. )
a.							a.
K ( x ) = 2x2		+ 2x2	+ 2x2 − x x − 3x x				K	(	x	)	=2x	2	+2x				2		+5x	2	+2x x			+ 6x x + 6x x
	1	2		3	1 3	2 3
											1					2			3			1	2		1	3	2	3
b.							b.
K ( x )=x2	+x2 +2x2			−6x x +2 6x x +2 6x x			K	(	x	)	=−3x			2	−x			2	+2 3x x −4x x −4 3x x
1		2	3	1 2	1 3	2 3
													1				2				1	2		1	3		2	3

№ 14.2. Привести уравнения поверхностей 2го порядка к каноническому виду и указать тип поверхностей ( № 14.1. )

a.	a.
2x2 + 2 y2 + 2z2 − xz − 3 yz =1	2x2 + 2 y2 +5z2 + 2xy + 6 xz + 6 yz =1
b.	b.

x2 +y2 +2z2 −6xy +2 6 xz +2 6 yz =0 (=±1) −3x2 − y2 +2 3 xy −4xz −4 3 yz =0 (=±1)

№ 14.3. Привести квадратичные формы к каноническому виду по методу Лагранжа. Найти преобразование ( № 14.1., № 14.2. )

a.																				a.
K ( x ) = 2x2							+ 2x2				+ 2x2 − x x − 3x x									K ( x )=2x2	+2x2		+5x2	+2x x + 6x x + 6x x
						1			2			3		1	3		2	3		1		2	3	1	2	1	3	2	3
b.																				b.
K	(	x	)	=x	2	+x		2	+2x		2	−6x x		+2 6x x			+2 6x x			K ( x ) =−3x2		−x2	+2 3x x −4x x −4 3x x
																					1	2		1 2		1 3		2 3
				1			2			3		1	2		1	3		2	3
№ 14.4.						Выяснить знакоопределенность квадратичных форм по критерию Сильвестра
( № 14.1., № 14.2., № 14.3. )
a.																				a.
K ( x ) = 2x2							+ 2x2				+ 2x2 − x x − 3x x									K ( x )=2x2	+2x2		+5x2	+2x x + 6x x + 6x x
						1			2			3		1	3		2	3		1		2	3	1	2	1	3	2	3
b.																				b.
K	(	x	)	=x	2	+x		2	+2x		2	−6x x		+2 6x x			+2 6x x			K ( x ) =−3x2		−x2	+2 3x x −4x x −4 3x x
																					1	2		1 2		1 3		2 3
				1			2			3		1	2		1	3		2	3

№ 14.5. Найти экстремумы функций 3х переменных

( № 14.1., № 14.2., № 14.3., № 14.4. )

a.	a.
f (x, y, z) = 2x2 + 2 y2 + 2z2 − xz − 3y z	f (x, y, z) =2x2 +2 y2 +5z2 +2xy + 6xz + 6 yz
b.	b.

f (x, y, z) =x2 +y2 +2z2 −6xy +2 6xz +2 6 yz f (x, y, z) = −3x2 −y2 +2 3xy −4xz −4 3yz

88

Теория

Матрица A квадратичной формы

K ( x ) = (	n n	+... +ak k xk2 +... + an n xn2 +... + (ai j + aj i )xi x j +...
	A x, x )= ∑∑ai j xi x j = a11 x12
	i =1 j=1	\\

для однозначного определения предполагается симметричной	2ai j
A′ = A ai j = a j i (ai j + a j i )= 2ai j
так что существует ортогональная матрица U :
U U′ = U′ U =I U′ = U −1

(столбцыкоторойобразуютортонормированныйбазисизсобственныхвекторовматрицы A ), приводящая A к диагональному виду (на диагонали стоят соответствующие собственные значения матрицы A )

A =U Λ U −1 =U Λ U′ U′ A U = Λ

Следовательно, ортогональное преобразование x =U x приводит квадратичную форму к каноническому виду (сумме квадратов)

K ( x )=( A x, x )=( AU x, U x )=( U′ A U x, x )=( Λ x, x )=λ1 x12 +...+λk xk2 +...+λn xn2

№ 14.1. a. Преобразуем квадратичную форму к каноническому виду.

		2		0	−1			x1
						2
K ( x ) = 2x12 + 2x22 + 2x32 − x1 x3 −	3 x2 x3 = ( 0			2	−	3	x2		,
						2
		−1		3
			−			2		x
		2		2
								3

x1x2x3

)

Найдем собственные значения матрицы A , т.е. корни характеристического полинома

				2 −λ		0		− 1
									2
	p	A	(λ) =det ( A −λI )=	0	2	−λ		−		3		= − (λ −1)(λ −2 )(λ −3 ) λ	1	=1,	λ	2	=2, λ	3	=3
									2
				− 1			3
					−			2	−λ
						2
				2

и соответствующие собственные векторы (заметим, что матрица третьего порядка A имеет три различных собственных значения, так что собственные подпространства одномерны и, очевидно, ортогональны друг другу)

						2 −1 0								−				1						1 0		− 1					x1									1										2
																		2								2														2							= 1
λ			=1		0 2 −1									−				3				~		±0 1	−		3					x			=	x				3					u					6
		1								3								2								2						2				3				2						1	4
						−	1	−						2 −1									0 0				0					x								1									2	2
										2
							2																									3
						2 − 2 0								−				1						0	0 1							x						−		3									−
																		2															1														= 1		2 3
λ	2		= 2		0 2 − 2									−				3				~	0		0		0					x			=	x				1					u					2
							1			3								2														2				2										2	4
						−		−						2 − 2									1		3		0					x								0										0
							2			2
																																3
						2 −3 0								−1										1 0		1					x1									−1									−	2
																		2								2														2							= 1
λ			= 3		0 2 −3									−				3				~		±0 1	±		3					x			=	x		−		3					u				− 6
	3										3							2								2						2				3				2						3	4
						−1		−						2 −3									0 ±0				0					x								1									2	2
							2			2																						3

89

Построим ортогональную матрицу
							2 −2 3 − 2
	u2 , u3		=	1
U = u1,				4			6	2 − 6
						2	2	0	2	2

Ортогональное преобразование

x = U x

приводит квадратичную форму к каноническому виду

K ( x ) = ( A x, x )= 2x12 + 2x22 + 2x32 − x1 x3 −

№ 14.1. b.
Квадратичная форма (см. № 12.1.,						№ 13.2.)
K ( x ) = x 2	+ x 2	+ 2x 2	−6x	1	x + 2 6x		1	x + 2
1	2	3			2			3

ортогональным преобразованием x =U x

U = u11 , u1 2 , u2 1 =

приводится к каноническому виду

3x2 x3 =1 x12 + 2 x22 + 3 x32 = (Λ x, x )= K ( x )

						1	−3 6			x1				x1
6x2 x3 = (					−3		1 6					,				)= →
										x2				x2
						6 6 2				x				x
										3				3
	−2		2		2	−	6
14		2	2		2	−	6
			0 ±2		3		2

→= 4 x 2

+ 4 x 2 − 4 x 2 = (Λ x, x )= K

n

( x )

1

2

3

№ 14.2.

2 го

Квадратичная

часть

уравнения

поверхности

порядка

представляет собой

квадратичную форму

(a

11

x2 + a

2 2

y2 + a

3 3

z2 + 2a

1 2

x y + 2a

1 3

x z + 2a

2 3

y z ) + (b x +b y +b z + c ) = 0

1

2

3

Собственным ортогональным преобразованием можно привести ее к каноническому виду

λ x 2 + µ y 2 + ν z 2 + ( ... ) = 0

Геометрический смысл ортогонального преобразования - поворот системы координат в пространстве на некоторый угол с возможным зеркальным отображением.

Для выяснения вида поверхности достаточно найти только собственные значения λ, µ, ν

№ 14.2. a.
Поверхность 2го порядка, задаваемая в старой системе координат { i ,														j,	k } уравнением
		2x 2 + 2 y 2 + 2z 2 − xz − 3y z =1
в новой системе координат {i ,			j,		k }
		2					−2 3							− 2
1				,	1				,	k = u3	=	1
i = u1 = 4		6			j = u2 = 4		2					4		− 6
	2 2						0						2 2

описывается уравнением ( № 14.1. a. ).

1 x 2 + 2 y 2 +3 z 2 =1

в котором легко узнается эллипсоид.

90