методичка черногор

Глава 2. Методы нелинейной электродинамики 2.3. Задачи для самостоятельного решения

2.3. Задачи для самостоятельного решения

2.1

Считая среду изотропной, недиспергирующей и недиссипативной, получить точное решение уравнений электродинамики, вычислить u ,E и H для

E

a) ε(E) = ε0(1 + αE)2, б) D = ∫ (1 + αE2 )2dE.

0

в) D = E + αE 3, г) ε(E) = ε0(1 + αE).

Считать, что до падения волны на среду (x<0, t<0)

E(0) = E0 cos k0 (x −ct).

2.2

Решить задачу об амплитудном самовоздействии волны при виде коэффициента поглощения:

a) α =			α0	, б) α = α0 (1+ aA),
	1		+ aA
в) α =			α0		, г) α =	α0		2 ,
	1		3			1+ aA	+bA
			+ aA

где А – амплитуда волны. Исследовать поведение решения в зависимости от величин и знаков a и b. Сделать оценки эффекта при |a|=A0-1, где A0 – амплитуда волны на границе.

2.3

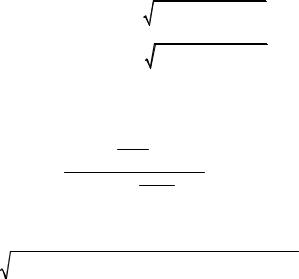
Вычислить множитель амплитудного взаимодействия сильной (1) и слабой (2) волн в глубине среды:

P =

A2

=

A2

ek20 .

12

A2‘

A20

Ограничиться распространением обеих волн в одном направлении. Принять

коэффициенты поглощения среды:

a) α

=

α10,20

,

б) α

= α

(1+ aA ),

1,2

1+ aA1

1,2

10,20

1

в) α

=

α10,20

,

г) α

= α

(1

+ aA +bA2 ).

1+ aA3

1,2

1,2

10,20

1

1

1

2.4

Получить формулу для нелинейной добавки к фазе за счет фазового самовоздействия. Принять, что:

39

Глава 2. Методы нелинейной электродинамики 2.3. Задачи для самостоятельного решения

	a) n(A) =1+ a1 A; α(A) =					α0	;
			1			+ a2 A
	б) n(A) =1+ a1 A; α(A) = α0 (1+ a2 A);
	в) n(A) =1+ a A2	; α(A) =			α0			;
	1			1+ a2 A
	г) n(A) =1+ a A2	; α(A) =				α0			.
			1			+ a A2
	1
						2

Оценить величину эффекта при |a1|=A0–1 (варианты а, б), |a1|=A0–2 (варианты в, г), |a2|=A0–1 (варианты а, б, в), |a2|=A0–2 (вариант г), где A0 – амплитуда волны на границе.

2.5

Получить формулу для нелинейной добавки к фазе слабой волны (2) за счет взаимодействия ее с сильной волной (1) и проанализировать результат. Обе волны распространяются в одном направлении. Принять следующие выражения для α1 и n2

													a) α1 = α10 (1+ aA1 ), n2 =1+bA1,
													б) α = α (1+ aA )−1,									n	=1+bA ,
													1					10	1			2	1	.
													в) α = α (1+ aA ),								n	=1+bA2 ,
													1					10	1		2		1
													г) α = α (1+ aA )−1							,		n	=1+bA2 .
													1					10	1			2	1
Для оценок использовать:
для вариантов a) и б)						a		=		b		= A−1						;
													10
для вариантов в) и г)		a				= A−1							;		b		= A−2 .
						10												10

Указание: ввести глубину затухания сильной волны в линейной теории L10=α10–1.

2.6

Уравнение эйконала для осесимметричного пучка в цилиндрической системе координат имеет вид

∂Ψ

∂Ψ 2

ε

нл

1

∂2 A

1 ∂A

2

+

=

+

2

+

.

∂z

k

2

∂r

εл

A

∂r

r ∂r

Не решая уравнения, оценить углы нелинейной рефракции и дифракции, получить условие для возникновения эффекта самоканалирования.

40

Глава 3. Ударные волны 3.1. Основные понятия и соотношения

3.УДАРНЫЕ ВОЛНЫ

3.1.Основные понятия и соотношения

Ударные волны (УВ) – это нелинейные стационарные волны, описывающие движение скачка какого-нибудь параметра волны или среды (плотности, давления и т. п.). Стационарность предполагает неизменность в процессе распространения, которая возникает в результате точной компенсации эффектов нелинейного укручения и диссипации. Профиль волны зависит только от “бегущей” координаты ξ = x −ut , где u – скорость волны. Эталонным

уравнением, описывающим УВ, является уравнение Бюргерса:

где ν – коэффициент вязкости.

vt + vvx

= νvxx ,

(3.1)

Пользуясь методом оценки производных, можно определить скорость u и ширину

фронта УВ ξ0. Переходя к ξ из (3.1), имеем:

′

′′

′

(3.2)

−uv + vv = νv , .

Полагая, что разность скоростей v на ±∞ равна v0, получим, что

v

v

v2

v′

0

;

v′′

0

; vv′

0

.

ξ

ξ2

ξ

0

0

0

Потребуем равенства по порядку величины первого и второго членов в (3.2), что т. е.

	−u	v					v2
			0					0		,
		ξ	0				ξ	0

откуда u v0. Аналогично из сравнения первого и третьего членов в (3.2) получим

−u	v0			ν	v0	.
	ξ	0			ξ2
				0

Отсюда ξ0 uν .

41

Глава 3. Ударные волны. 3.2. Примеры

3.2. Примеры

Пример 1

Ударная волна описывается

уравнением

Бюргерса vt + vvx = νvxx . Найти и

проанализировать решение, если v(−∞) = v2 ; v(+∞) = v1; v′(±∞) = 0;

причем v1<v2.

Решение

Введем переменную ξ = x − ut . Тогда

∂v

dv ∂ξ

′

∂v

dv ∂ξ dv

′

vt ≡

∂t

= dξ ∂t

= −uv , vx

≡

∂x = dξ ∂x

= dξ

= v ,

vxx =

∂

dv

d ∂ξ dv

dv ∂2ξ

′′

=

+

dξ ∂x

2 = v ,

∂x dξ

dξ ∂x dξ

и нелинейное дифференциальное уравнение второго порядка в частных производных превращается в дифференциальное уравнение, но уже в обычных производных относительно

функции v(ξ):

−uv′+ vv′= νv′′, v(−∞) = v2 ; v(+∞) = v1; v′(±∞) = 0.

Выделим полную производную и проинтегрируем

−uv + 12 v2 = νv′+C.

Используем граничные условия для определения неизвестных констант u и C:

−uv			+	1 v2		= C
		2		2 2		.
				1 v2
−uv +						= C
	1			2	1

Отсюда u = 12 (v1 + v2 ); C = − 12 v1v2 . Тогда

2νv′ = (v − v1 )(v − v2 ).

Так как v2 ≥ v ≥ v1 , то правая часть всегда неположительна, поэтому и v′ ≤ 0 . Разделив переменные и проинтегрировав, получаем:

	1	ln		v - v2		=	ξ	+C .
	v − v			v - v			2ν
								1
	1			1

Выберая точку отсчета ξ, положим C1=0. С учетом этого:

	v − v2		= e	ξ	(v2	−v1 ) .
				2v
	v − v
	1

Легко убедиться, что v − v2 < 0. Поэтому окончательный вид решения таков: v − v1

v(ξ) =	v e ξξ0	+ v		2	,	ξ		=		2ν		.
	1						0
	1+e	ξξ	0						v	2	− v
											1

Видно, что чем больше ν, тем более размытым будет фронт ударной волны.

42

Глава 3. Ударные волны. 3.2. Примеры

Пример 2

Ударная волна описывается уравнением

v + 3αv2v

x

= νv

xx

.

(3.3)

t

Найти и проанализировать решение, если

v(−∞) = v2 ; v(+∞) = v1; v′(±∞) = 0.

Решение

Введем переменную ξ= x −ut.

Тогда

vt ≡

∂v

dv ∂ξ

′

∂t

= dξ ∂t

= −uv

,

∂v

d v ∂ξ

d v

′

vx ≡

∂x

= dξ ∂x

= dξ

= v ,

vxx =

∂

dv

=

d ∂ξ

dv

+

dv

∂2ξ

′′

2

dξ ∂x

dξ ∂x

= v ,

∂x dξ

dξ

Уравнение (3.3) принимает вид

−uv′+ 3αv2v′= νv′′,

v(−∞) = v2 ; v(+∞) = v1; v′(±∞) = 0.

Выделим полную производную и проинтегрируем

(−uv +αv

3

′

′ ′

)

= (νv )

,

−uv +αv

3

′

+С.

(3.3.А)

= νv

Используем граничные условия для определения неизвестных констант u и C:

								= C,
					−uv2 +αv2
							3
					−uv +αv3			= C.
Отсюда u = α(v22 + v1v2 + v12 );						1	1
			C =−αv1v2 (v1 + v2 ).
Тогда	ν	v′ = (v − v1 )(v − vk1 )(v − vk 2 ), где
	α				(v1+ v12			2 (v1+v 2 ))< 0,
		vk1 = −	1				+ 4v
			2		(v1− v12			2 (v1+v 2 ))> 0.
		vk 2 = −		1			+ 4v
			2

Можно заметить, что правая часть всегда меньше или равна 0, следовательно и v′ ≤ 0 , а значит v2>v1. Разделив переменные, проинтегрировав и положим константу интегрирования равной нулю, выбрав соответствующим образом точки отсчета по ξ, получаем:

v1−vk 2

(v − vk1 )vk 2 −v1 (vk 2 − v) = eαξ2v (vk 2 −vk1 )2 .

vk 2 −vk1

(v − v1 ) v1−vk1

Разрешить такое уравнение относительно v(ξ) при произвольном виде v2 и v1 не удается. Положим v2>>v1. Тогда решение примет вид:

v(ξ) =	v1 +	v12 +(1+exp(−2ξ/ ξ0 ))(v22 exp(−2ξ/ ξ0 ) − v12 )	,	ξ0 = ν/ 2v22 .
		1+exp(−2ξ/ ξ0 )

43

Глава 3. Ударные волны. 3.2. Примеры

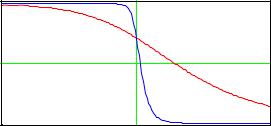
0

Рис.3.1. Вид решения v(ξ) .

На рисунке графику с более крутым профилем соответствует меньшее значение вязкости

Очевидно, что чем больше ν , тем более размытым становится фронт ударной волны.

44

Глава 3. Ударные волны.

3.3. Задачи для самостоятельного решения

3.3. Задачи для самостоятельного решения

3.1

Ударная волна описывается уравнением Бюргерса: vt + vvx = νvxx .

Найти и проанализировать решение, если граничные условия имеют вид:

						′			= 0, ξ = x −ut;
a) v(−∞) = v0 , v(+∞) = 0, v							(±∞)
	1						, v′(±∞) = 0, ξ = x −ut;
б) v(−∞) = v0 , v(+∞) =				v0
		2
							′
в) v(−∞) = v0 , v(+∞) = 0, v (±∞) = 0, ξ = x +ut;
г) v(−∞) = v0 , v(+∞) =	1		v0			,	v′(±∞) = 0, ξ = x +ut.
	2
3.2
Ударная волна описывается уравнением:
v + 3αv2v					x	= νv		xx	.
t

Найти и проанализировать решение, если граничные условия имеют вид: a) v(−∞) = 2v0 , v(+∞) = 0, v′(±∞) = 0, ξ = x −ut;

б) v(−∞) = v0 , v(+∞) = 0, v′(±∞) = 0, ξ = x −ut; в) v(−∞) = 2v0 , v(+∞) = 0, v′(±∞) = 0, ξ = x +ut; г) v(−∞) = v0 , v(+∞) = 0, v′(±∞) = 0, ξ = x +ut.

3.3

Не решая уравнения Бюргерса

vt + vvx = νvxx ,

оценить скорость и ширину фронта ударной волны, используя метод оценки производных. Граничные условия имеют вид:

a) v(−∞) = v0 , v(+∞) =					′		ξ = x −ut;
	0, v					(±∞) = 0,
б) v(−∞) = v0 , v(+∞) =	1			v0	,	v′(±∞) = 0, ξ = x −ut;
		2
в) v(−∞) = v0 , v(+∞) =					′		ξ = x +ut;
	0, v					(±∞) = 0,
г) v(−∞) = v0 , v(+∞) =	1		v0		,	v′(±∞) = 0, ξ = x +ut.
	2

3.4

Найти и проанализировать решение уравнения для ударной волны с затуханием: vt + vvx = νvxx +αv, α > 0.

Граничные условия имеют вид:

45

Глава 3. Ударные волны.

3.3. Задачи для самостоятельного решения

a) v(0) = v0 , v(+∞) =						′
			0, v				(±∞) = 0, ξ = x −ut;
б) v(0) = v0 , v(+∞) =						′
			0, v (±∞) = 0, ξ = x +ut;
в) v(0) = v0 , v(+∞) =				v0		,	′	ξ = x −ut;
				2			v (±∞) = 0,
г) v(0) = v0 , v(+∞) =				v0			′	ξ = x +ut.
				2		, v (±∞) = 0,
3.5
Не решая уравнения для ударных волн с затуханием:
v + vv	x	= νv		xx	+ γv2 , γ > 0.
t

оценить глубину затухания волны Lзат и сравнить Lзат с шириной фронта ξ0, если v=v(ξ), v(ξ=− ∞)=v0, v(ξ=+ ∞)=0.

3.6

Найти и проанализировать решение уравнения Бюргерса vt + (C0 + v)vx = νvxx ,

где С0=const при

a) v(−∞) = v0 , v(+∞) = 0, v′(±∞) = 0, ξ = x −ut; б) v(−∞) = v0 , v(+∞) = 12 v0 , v′(±∞) = 0, ξ = x −ut; в) v(−∞) = v0 , v(+∞) = 0, v′(±∞) = 0, ξ = x +ut;

г) v(−∞) = v0 , v(+∞) = 12 v0 , v′(±∞) = 0, ξ = x +ut.

3.7

Не решая уравнения

vt + 3αv2 vx = νvxx ,

оценить скорость и ширину фронта ударной волны. Граничные условия имеют вид a)v(−∞) = v0 , v(+∞) = 0, v′(±∞) = 0, ξ = x −ut;

б)v(−∞) = 2v0 , v(+∞) = 0, v′(±∞) = 0, ξ = x −ut; в)v(−∞) = v0 , v(+∞) = 0, v′(±∞) = 0, ξ = x +ut; г)v(−∞) = 2v0 , v(+∞) = 0, v′(±∞) = 0, ξ = x +ut.

46

Глава 4. Солитоны 4.1. Основные понятия и соотношения

4.СОЛИТОНЫ

4.1.Основные понятия и соотношения

Под классическим солитоном понимается уединенная стационарная волна, описываемая

решением уравнения Кортевега – де Вриза (КдВ) вида:

vt + vvx + βvxxx

= 0, β = const>0.

(4.1)

Солитон возникает в результате компенсации нелинейного укручения профиля волны

дисперсионным расплыванием волнового пакета.

Для ξ = x − ut при

v

ξ=±∞ = v′

ξ=±∞ = v′′

ξ=±∞ = 0

решение (4.1) имеет вид:

v(0)

v(ξ) =

,

(4.2)

ξ

ch2

ξ0

где

v(0) = 3u,

ξ0 = 2

β.

(4.3)

u

Амплитуду v(0) и ширину ξ0 солитона можно оценить, используя метод оценки

производных. Для этого при помощи подстановки

ξ = x − ut

перейдем от уравнения (4.1) к

следующему соотношению:

′

′

′′′

= 0.

−uv

+ vv

+βv

Учитывая, что

′

v(0)

,

′′′

v(0)

,

из условий равенства первого и второго, а также

v

ξ

v

ξ3

0

0

первого и третьего членов соответственно получим

u

v(0)

v2 (0)

, v(0)

u;

(4.4)

ξ0

ξ0

u v(0)

βv(0) , ξ

0

β.

(4.5)

ξ0

ξ30

u

Сравнение (4.4) и (4.5) с точными значениями (4.3) подтверждает реальность оценок.

В настоящее время под солитонами понимаются локализованные решения нелинейных уравнений, удовлетворяющие определенным законам сохранения.

47

Глава 4. Солитоны 4.1. Основные понятия и соотношения

Солитоноподобными решениями обладает уравнение Гордона вида:

vxx + vtt = f (v),

где f(v) – нелинейная функция.

Солитон огибающей описывается нелинейным уравнением Шредингера (НуШ):

iv + v

xx

+βv

v

2 = 0,

t

(4.6)

Его решение ищется в виде

β > 0,

v

ξ=±∞ = v′

ξ=±∞ = 0.

v(x,t) = w(x −u t)eiϕ( x−u2t ) .

1

Из (4.6) для w и ϕ следуют уравнения

u2wϕ′+ w′′− wϕ′2 +βw3 = 0,

(4.7)

′

′

′

′′

(4.8)

−u1w

+2w ϕ + wϕ = 0.

Умножением на 2w ≠ 0 из (4.8) получаем уравнение:

2

′

′

= 0,

w

(2ϕ −u1 )

откуда

w2 (2ϕ′−u1 )= C1.

Ввиду произвола в выборе w и ϕ можно положить С1=0. Тогда

ϕ =

1 u ξ+C

.

2

1

2

По той же причине можно считать С2=0, и уравнение (4.7) примет вид:

1

′′

u

2

3

1

+βw

= 0.

2

u1u2 w + w

− w

2

w

′

После умножения на

оно легко интегрируется. В конечном итоге (4.6) оказывается

таковым:

v (0)

u1

v (x,t )=

i

(x−u2t )

e

2

,

ch

x −u1t

ξ

0

где

u

(u −2u

)

1

(

)

2

0

1 (

1

2 )

−1

v

1

1

2

0

=

2β

; ξ

=

u u

−2u

2 .

48