методичка черногор

Глава 4. Солитоны 4.2. Примеры

4.2. Примеры

Пример 1

Найти солитоноподобное решение уравнения “синус – Гордона”:

vtt + vxx	= sin v,
v(±∞)= v′(±∞)= 0.
Решение	(	2	)	v	′′	= sin v.
Введем переменную ξ = x −ut . Тогда	1+u

Домножим на v′, выделим полную производную и проинтегрируем: 12 (1+u2 )(v′2 )′ = −(cos v)′,

12 (1+u2 )v′2 = −cos v +C.

Из граничных условий следует, что С = 1. Тогда

	v	′	= ±	1		v
				1+u2	2sin 2 .

Отсюда после разделения переменных и последующего интегрирования получаем:

±	ξ
v± (ξ)= 4arctg e	1+u2 ,

причем постоянная интегрирования полагается равной нулю в результате выбора начала отсчета по ξ.

6.25607
v1( x)		Рис. 4.1. Вид решения v± (ξ).
v2( x)
0.02712		100
-100	x

Решение v± (ξ) (рис. 4.1) – солитоноподобно, причем v+ называют солитоном, а v− – антисолитоном. Вычислим производную по ξ:

v′± (ξ)= ±		2	ch−1	ξ	.
		+u2
1				1+u2

Видно, что v′± (ξ) описывается солитоноподобным решением (рис. 4.2).

49

Глава 4. Солитоны 4.2. Примеры

0.0998752
vp1( x)		Рис. 4.2. Вид v′± (ξ).
vp2( x)
-0.0998752
-100	x	100

Пример 2

Показать, что решение в виде

v (ξ)= v0ch−2

ξ

также

удовлетворяет линейному

ξ0

уравнению гиперболического типа

v

−u2 v

xx

= 0,

ξ = x −ut.

(4.9)

tt

Решение

Докажем, что всякая функция v = v(ξ), где ξ = x – ut, есть решением такого линейного

уравнения.

∂v

d v ∂ξ

′

vt ≡

∂t

= dξ ∂t

= −uv ,

vtt =

∂

d v ∂ξ

d 2 v ∂ξ

dv

∂2ξ

2

′′

=

2

+

2

= u

∂t

dξ ∂t

dξ

∂t

dξ

∂t

∂v

d v ∂ξ

′

vx ≡

∂x

= dξ ∂x

= v

,

vxx =

∂

d v ∂ξ

d 2 v ∂ξ

dv

∂2ξ

= v′′.

=

dξ

2

+

dξ

∂x

2

∂x dξ ∂x

∂x

Подставим вычисленные производные в (4.9). Видно, что (4.9) обращается в тождество вне зависимости от конкретного вида функции v(ξ). Следовательно, любая v(ξ), в том числе и заданного вида, является решением уравнения (4.9).

50

Глава 4. Солитоны 4.3. Задачи для самостоятельного решения

4.3. Задачи для самостоятельного решения

4.1

Найти солитоноподобное решение модифицированного уравнения КдВ (мКдВ)

v +6αv 2v	x	+βv	xxx	= 0,	α > 0, β > 0,
t

v (±∞)= v′(±∞)= v′′(±∞)= 0, a) ξ = x −ut,

б) ξ = x +ut, u < 0.

4.2

Оценить амплитуду v0 и ширину ξ0 солитона, не решая уравнения мКдВ

v +6αv 2v	x	+βv	xxx	= 0,	α > 0, β > 0;
t

v(±∞)= v′(±∞)= v′′(±∞)= 0.

Сравнить с точным решением. Принять

a)ξ = x −ut,

б)ξ = x +ut.

4.3

Оценить амплитуду v0 и ширину ξ0 солитона, не решая уравнения КдВ

vt + vvx +βvxxx = 0,	α > 0, β > 0;
v (±∞)= v′(±∞)= v′′(±∞)= 0.

Сравнить с точным решением. Принять

a) ξ = x −ut,

б) ξ = x +ut.

4.4

Показать, что решение в виде солитона огибающей

удовлетворяет линейному уравнению гиперболического типа:

vtt −u2 vxx = 0.

Принять

a) ξ = x −ut,

б) ξ = x +ut.

4.5

Найти солитоноподобное решение уравнения Гордона типа:

vtt + vxx = 2v3 ,

v(±∞)= v′(±∞)= 0.

Принять

	v(ξ)= v0ch−1	ξ	также
		ξ
	0

51

Глава 4. Солитоны 4.3. Задачи для самостоятельного решения

a) ξ = x −ut,

б) ξ = x +ut.

4.6

Найти и проанализировать решение нелинейного уравнения Шредингера вида: ivt + vxx +βv v 2 = 0,

v(±∞)= v′(±∞)= 0, β > 0, ξ1 = x +u1t, ξ2 = x +u2t.

4.7
Показать, что уравнение
v + v		v	x	= Dv	xx	+ 2αv3	−βv,
t	0
v0 ,α,β, D = const,					α > 0 , β > 0 , D > 0

с граничными условиями v(±∞)= v′(±∞)= 0 описывает диссипативный солитон.

4.8

Показать, что уравнение мКдВ сводится к уравнению КдВ подстановкой w = v2 .

4.9

Найти солитоноподобное решение уравнения с нулевыми условиями на функцию v(ξ) и ее первые две производные при ξ = ±∞ :

а)	vt + vvx +βvxxt		= 0,	β < 0,
б)	vt	+ vvx +βvxtt	= 0,	β > 0,
в)	vt	+ vvx +βvttt	= 0,	β < 0,
г)	vx + vvt +βvttt		= 0,	β > 0.

4.10

Найти солитоноподобное решение уравнения с нулевыми условиями на функцию v(ξ) и ее первые три производные при ξ = ±∞ :

а) −v +

α (v2 )

xx

+βv

xxxx

= 0,

α > 0 , β > 0 ,

tt

2

б) v +

α (v2 )

xt

+βv

xxxx

= 0,

α > 0 , β < 0 ,

tt

2

в)

vxx

+

α

(v2 )tt

+βvxxxx

= 0,

α < 0 ,

β < 0 ,

2

г)

vxt

+

α

(v2 )tt

+βvxxxx

= 0,

α > 0 ,

β > 0 .

2

4.11

Найти солитоноподобное решение уравнения с нулевыми условиями на функцию v(ξ) и ее первые три производные при ξ = ±∞ :

52

Глава 4. Солитоны 4.3. Задачи для самостоятельного решения

а) v +	α (v2 )	xx		+βv	xxxt	= 0,	α < 0 , β > 0 ,
tt	2
б) v +	α (v2 )	xx		+βv	xxtt	= 0,	α < 0 , β < 0 ,
tt	2
в) v +	α (v2 )	xx		+βv	xttt	= 0,	α < 0 , β > 0 ,
tt	2
г) v +	α (v2 )		xx	+βv = 0,			α < 0 , β < 0 .
tt	2				tttt

4.12

Выяснить, имеет ли солитоноподобное решение уравнение КдВ с нулевыми условиями

на функцию v(ξ) и ее первые две производные при ξ = ±∞,							если β < 0 :
	а) vt + vvx +βvxxx = 0,
	б) v +αv2 v		x	+βv	xxx	= 0.
	t
Сравнить полученное решение с решением для β > 0.
4.13
Показать, что уравнения
а) vt	+αvx	+ vvx +βvxxx			= 0,		β > 0,
б) vt	+αvt	+ vvx +βvxxx			= 0, β > 0

сводятся к уравнению КдВ. Найти их решения. Какие условия налагаются на α?

53

Глава 5. Когерентное взаимодействие волн. Неустойчивости. 5.1. Основные понятия и соотношения

5. КОГЕРЕНТНОЕ ВЗАИМОДЕЙСТВИЕ ВОЛН. НЕУСТОЙЧИВОСТИ

5.1. Основные понятия и соотношения

Когерентное взаимодействие волн возникает благодаря передаче энергии волны накачки с амплитудой А0 другим волнам. Посредником во взаимодействии выступает среда.

Рассмотрим трехволновое взаимодействие, описываемое системой уравнений:

	dA1		= γ A A −ν A ,							(5.1)
dt		1			0	2	1		1,
dA			= γ2 A0 A1 −ν2 A2 ,							(5.2)
	2
	dt
	dA0		= γ	0	A A		−ν	0	A .	(5.3)
					1	2			0
dt

Здесь A1 и A2 – амплитуды возбуждаемых волн.

Пороговое значение амплитуды волны накачки находится из (5.1) и (5.2)							при	d	= 0 и
								dt
равно:
		A0(0) =	ν1ν2		.
			γ γ	2
			1
Если потери в системе отсутствуют, т. е. ν1=ν2=ν0=0, то процесс взаимодействия
является беспороговым ( A(0) = 0 ).
	0
Если A1,2	<< A0 ,то	применим несамосогласованный подход.				При этом достаточно
решения уравнений (5.1) и (5.2). Задача сводится к двухволновому взаимодействию.
Когерентное взаимодействие может привести к экспоненциальному росту							A1,2 (t) , т. е. к
генерации неустойчивости. Она имеет стадии: линейную, когда						A0 ( t )	уменьшается
незначительно, а	A1,2 (t)	растут экспоненциально с инкрементом				λ; нелинейную, когда

экспоненциальный рост A1,2 (t) прекращается и A1,2 (t) → A1∞,2∞ в результате истощения энергии волны накачки.

54

Глава 5. Когерентное взаимодействие волн. Неустойчивости.

5.1.Основные понятия и соотношения

Вотсутствие потерь λ = γ1γ2 A0 , а при их наличии:

λ = − ν1 +ν2 +	ν1 +ν2		2	+ A2	γ	γ	2	−ν ν	.
2		2		0	1			1 2

В системе без потерь справедливы соотношения Мэнли – Роу, являющиеся разновидностью закона сохранения энергии:

A2

− A2

A2

− A2

A2 − A2

1

10

=

2

20

=

0

00

= const,

(5.4)

γ

γ

γ

1

2

0

где γ0 < 0, γ1,2

> 0.

Взрывная неустойчивость возникает, когда приток энергии растет быстрее, чем ее

потери. Она описывается, например, таким уравнением:

dA

=γA2

−νA; A

t=0

= A(0),

γ > 0,

ν > 0.

(5.5)

Тогда

dt

A(t) =

A(0) A(0)

,

(0)

− A(0))e

νt

A(0) +(A

где A(0)

ν

порога. При А(0)<A(0)

и νt >>1 имеем A(t )→ 0 . Если же

= γ – значение

А(0)>A(0) , то наступает момент t0, при котором

A(t0 )→ ∞

(генерируется

взрывная

неустойчивость). Для модели (5.5) справедливо выражение:

A(0)

t

=

1 ln

.

0

(0)

ν

A(0)

− A

Реально взрывная неустойчивость ограничивается появлением дополнительного источника потерь, который был несущественным при достаточно малых временах. Нелинейная стадия таких неустойчивостей описывается, например, таким уравнением:

d

dAdt =γA2 −νA −βA3 , β > 0 .

γ

(5.6)

Из (5.6) при

= 0 следуют три решения: А =0 (тривиальное, волны нет),

A ≈

≡ A –

β

dt

0

1

∞

стационарное (максимальное)

значение амплитуды,

A ≈

ν

≡ A(0) – пороговое

значение

2

γ

(считается, что 4βν << γ2 ). Время выхода А(t) на значение, близкое к A∞ , равно

t∞ = (βA∞2 )−1 .

(5.7)

При изучении неустойчивостей под переменной t понимается не обязательно время, ею

′

x

может быть координата , а также время в подвижной системе

координат

t

= t − vг

, где vг –

групповая скорость волнового пакета.

55

Глава 5. Когерентное взаимодействие волн. Неустойчивости. 5.2. Примеры

5.2. Примеры

Пример 1

Решить следующую задачу о двухволновом взаимодействии:

dA1

= γ

A A

;

A

|

= 0,

(5.8)

dt

1

0

2

1

t =0

dA2

= −γ

2

A A

;

A

|

= A

(0) .

(5.9)

dt

1

2

2

t=0

2

Считать,

γ1,2 > 0 . Получить и проанализировать соотношение Мэнли – Роу, а

также

выражения для A1(t) и A2(t).

Решение

Разделим (5.8) на (5.9) и получим

A0

dA1

= −

γ1

.

dA

γ

2

A

Отсюда

2

1

1 A2

+

A A

= C.

1

0

2

(0)

2 γ1

γ2

Из начальных условий

C =

A0 A2

. Тогда

γ

γ

2

A12 (t )

=

A

A2 (0)− A2 (t )

.

2γ1

0

γ2

Это уравнение представляет собой соотношение Мэнли-Роу. Отсюда

A2 (t )= −

γ

2

A12 (t )

+ A2 (0).

(5.10)

A

2γ

1

Подставим (5.10) в (5.8):

0

dA1

γ2

2

= γ

A A

(

0)

1

−

A1

.

(0)

dt

1 0 2

2γ

1

A A

0

2

Пусть

d

= 0. Тогда

A2

=

2γ1 A2 (0)A0

.

dt

1 ∞

γ2

Уравнение для

A1 / A2

примет вид:

(0)

d

A

A0 A2

A2

1

= γ1

1−

1

.

dt A

A

A

2

1∞

1∞

1 ∞

Разделим переменные:

d

A

1

A A

(0)

A

1∞

= γ1

0 2

dt ,

2

A

1−

A

1

1∞

A2

1 ∞

56

Глава 5. Когерентное взаимодействие волн. Неустойчивости. 5.2. Примеры

отсюда

				A A	(0)t
	A1	(t )= A1∞th	γ1	0 2		+C1		,
				A1∞

Из начальных условий: A1 (0)= A1∞th(C1 ) = 0, что дает Таким образом

t0 =		A1∞			.
	γ	A A		(0)
1		0	2

С1 = 0.

A1 (t )= A1∞th	t	,	A2	(t )= A2	(0)ch−2	t	.
	t0					t0

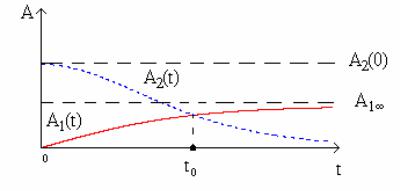
Графики решений A1 (t) и A2 (t) показаны на рис. 5.1.

Рис. 5.1. Вид решений А1(t), A2(t).

Легко убедиться, что время развития неустойчивости равно t0 .

Энергия одной волны передается другой волне. Такое возможно только в случае, если среда была изменена волной накачки с амплитудой A0 ≠ 0 . При А0 = 0 никакого взаимодействия не будет.

Пример 2

Исследовать генерацию второй гармоники в нелинейной среде, описываемую системой укороченных уравнений:

	dA1		= γ	A2 A ,						A							= A			(0),	γ		< 0,
	dx		1		2	1				1			x		=0				1			1			(5.11)
	dA2
			= γ		A2 A			,			A							= A (0),				γ		>	0.
	dx			2	1	2				2					x=0					2			2
Решение
Соотношения Мэнли – Роу в данном случае имеют вид
	A2	− A2		(0)		=		A2 − A2									(0)		.						(5.12)
	1		1						2						2
Отсюда			γ1										γ2
							γ2
	A2	= A2		(0) +							(A2 − A2								(0)) .						(5.13)
2			2					γ	1	1							1
Подставляя (5.13) в (5.11), получим
	dA1		= γ	A (A2 (0) +												γ2		(A2		− A2	(0))).				(5.14)
	dx		1		1	2										γ1	1			1

57

Глава 5. Когерентное взаимодействие волн. Неустойчивости. 5.2. Примеры

При x → ∞ или

d

= 0

справедливо такое решение для A (∞) ≡ A

:

dx

1

1∞

γ1

A2 =

A2 (0) −

A2 (0) .

(5.15)

1∞

1

γ

2

2

С учетом (5.15) уравнение (5.14) принимает вид:

dA1

= γ

A (A2 − A2 ) .

dx

2

1

1

1∞

Разделяя переменные и интегрируя, имеем

A (x) = A2 (0) +

γ

2

A2

A2 ex / x0

,

2∞

γ

A2

+ A2 (0)(ex / x0

−1)

1

1

1

20

2∞

2

где

γ2

γ2

x = −(γ A2

)−1, A2

= A2

(0) −

A2

(0), A2 = A2

(0) −

A2 (0).

0

1 2∞

2∞

2∞

γ

1

1

2∞

2

γ

1

1

С учетом A1 (x) из (5.12) получаем

A2 (x) = A2 (0)

A2 ex / x0

.

2∞

A2

+ A2 (0)(ex / x0

−1)

2∞

2

В соответствии с полученными решениями амплитуда волны накачки A1 (x)

убывает от

A1 (0)

до A1∞ , а амплитуда второй гармоники растет от A2 (0)

до A2∞ .

Пример 3

Исследовать взрывную неустойчивость, описываемую уравнением

dA = γA2

−νA; γ,ν = 0,

A(0)= A(0),

dt

где А(0) – пороговое значение.

Решение

γA(0)2 −νA(0) = 0 и

Пороговое значение

находится

из

соотношения

равняется

(0)

ν

A

= γ . Тогда исходное соотношение примет вид

dA

=

γA(A − A(0) ).

dt

Проинтегрируем это уравнение методом разделения переменных:

A

= C exp(−A(0) γt) .

A − A

(0)

Из начального условия следует, что

A(0)

C =

.

(0)

A(0) − A

Тогда

A(0)

A(t) =

.

(0)

1− 1

−

A

exp(A(0) γt)

A(0)

58