1.2. Барометрическая формула

Умножив обе части распределения Больцмана на kT, получим со­гласно основному уравнению МКТ, что давление где— молярная масса,R — универсальная газовая постоянная. Это так называемая барометрическая формула. Она строго спра­ведлива для идеального газа, температура которого не зави­сит от высоты (изотермическая атмосфера). На рис. 2 пока­заны два графика зависимости давления от высоты z при разных температурах . Следует обратить внимание на то, что в отличие от распределе­ний n(z), кривые p(z) на рис. 2 начинаются в одной точке независимо от температуры. Это не случайно и имеет простое объяснение .

Рассмотрим, как ведет себя центр масс газа в поле тяжести. При анализе ситуации, изображенной на рис. 2, мы приходим к выводу, что в результате повышения температуры от до центр масс газа перемещается вверх. Возникает вопрос: под действием какой внешней силы? На первый взгляд вроде ниче­го не изменилось — ни сила тяжести, ни сила реакции со сто­роны поверхности Земли (ведь давление осталось прежним). На самом же деле в процессе нагревания газа равновесие нарушается , вторая сила оказывается большей по модулю. Она на­правлена вверх и вызывает перемещение центра масс.

Представим барометрическую формулу в виде , где— это высота, на которой давление убывает в е раз. Значение h играет роль характерной толщины атмосферы. При = 20 г/моль и Т = 280 К величина h = 8 км. По сравнению с радиусом Земли атмосфера — тонкая пленочка (что и позволяет при получении барометрической формулы счи­тать ускорение g не зависящим от высоты).

Из распределения Больцмана возникает следующий «парадокс»: почему в поле тяжести при движении моле­кул вверх их кинетическая энергия уменьшается, а температу­ра остается прежней, т.е. средняя кинетическая энергия не ме­няется, а при движении вниз кинетическая энергия всех моле­кул увеличивается, а средняя их энергия остается той же? Этот «парадокс» был разъяснен уже Максвеллом. При движении вверх молекулы действительно замедляют­ся, но при этом наиболее медленные молекулы выбывают из потока частиц. При движении же вниз, наоборот, молекулы не только ускоряются, но одновременно их поток пополняется бо­лее медленными молекулами. В результате средняя скорость теплового движения молекул остается неизменной. Сила тяже­сти меняет лишь концентрацию молекул на разных высотах, но не температуру газа. И закон распределения Больцмана как раз и выводится из условия, чтобы температура газа оставалась всюду одной и той же.

1.3. Диффузия в газах

Предположим, что в единице объема двухкомпонентной газовой смеси содержится п₁ молекул одного вида и п₂ молекул другого вида. Полное число молекул в единице объема равно п = п₁ + п₂. Отно­шение:

н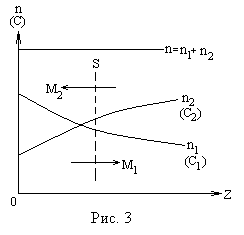азываетсяотносительной концентрацией моле­кул i-го вида.

Допустим, что в направлении оси Z создаются градиенты кон­центраций dc₁/dz и dc₂/dz, причем dc₁/dz = — dc₂/dz (рис. 3). Тогда

так что п, а следовательно, и р постоянны (р = nkT). В этом случае газодинамических потоков не возникает. Однако вследствие теплового движения молекул будет происходить процесс вы­равнивания концентраций, сопровож­дающийся переносом массы каждой из компонент в направлении убывания ее концентрации. Этот процесс носит наз­вание диффузии. Диффузия наблю­дается также в жидких и твердых телах. Поток молекул i-го вида через перпен­дикулярную к оси Z поверхность S оп­ределяется выражением

(3)

где D — коэффициент пропорциональности, называемый коэф­фициентом диффузии. Знак минус указывает, что поток молекул направлен в сторону убывания концентрации. Умножив обе части этого равенства на массу молекулы i-го вида m_i, получим выражение для потока массы i-й компоненты:

(4)

где ρ_i = n_im_i— парциальная плотность i-й компо­ненты; ее называют также абсолютной концентра­цией.

Формулы (3) и (4) представляют собой эмпирические урав­нения диффузии. Их называют также законом Фика.

Получим уравнение диффузии, основываясь на молекулярно-кинетических представлениях, причем для упрощения расчетов будем считать, что молекулы обеих компонент мало отли­чаются по массе (m₁ m₂ m ) и имеют практически одинаковые эффективные сечения (σ₁ σ₂ σ). В этом случае молекулам обеих компонент можно приписывать одинаковую среднюю скорость теп­лового движения, а среднюю длину свободного пробега вычис­лять по формуле

где n = n₁ + n₂.

Пусть изменение концентрации первой компоненты вдоль оси Z задано функцией n₁ = n₁ (z).

Через поверхностьS будут пролетать в положительном направ­лении оси Z молекулы, претерпевшие последнее соударение на раз­личных расстояниях отS. Разобьем все пространство слева от S на слои толщины d (рис. 4). Полный по­ток молекул через поверхность S можно получить, просуммировав по­токи, создаваемые молекулами, испы­тавшими последнее соударение в та­ких слоях.

Из слоя толщины dначинают свой полет к поверхностиS те мо­лекулы первой компоненты, которые претерпевают в этом слое столкнове­ние с другими молекулами. Их чис­ло равно

где z — координата плоскости S (d/λ есть вероят­ность претерпеть соударение на пути d). Эти молекулы создают через поверхностьS (z – )) поток

Из числа молекул, летящих в этом потоке, достигает поверх­ности S без столкновений и, следовательно, проникает в пространство, расположенное справа от S, количество молекул, равное

.

(е^–l/λ есть вероятность того, что молекула пролетает путь без столкновений). Знак «+» приdN₁ указывает на то, что имеются в виду молекулы, летящие в положительном направлении оси z.

Полный поток молекул первой компоненты через поверхность S получим, проинтегрировав это выражение по :

Воспользовавшись быстрым спадом экспоненты и малостью λ, пред­ставим стоящую под знаком интеграла функцию n₁(z – ) в виде

где dn₁/dz — производная в точке с координатой z. Тогда

Первый интеграл есть единица, второй равен λ. Следовательно,

Поток молекул первой ком­поненты, летящих через поверхность S в отрицательном направле­нии оси z,

Результирующий поток молекул первой компоненты через по­верхность S в направлении оси z равен разности этих потоков

(5)

Мы получили уравнение (3), причем коэффициент диффузии

(6)

При этом коэффициент диффузии для обеих компонент имеет одинаковое значение.

Подставив в (5) выражения для и λ, можно получить, что

Коэффициент диффузии оказывается обратно пропорциональным числу молекул в единице объема, а следовательно, и давлению р:

С ростом температуры коэффициент диффузии растет пропорционально

Так как мы полагали молекулы обеих компонент одинаковыми по массе к эффективному сечению, (6) представляет собой, по суще­ству, выражение для коэффициента самодиффузии, т. е. диффузии молекул некоторого газа в среде молекул того же газа. Явление са­модиффузии можно было бы наблюдать, пометив каким-то способом часть молекул однородного газа. Тогда в случае, если бы концентра­ция меченых молекул и молекул, не несущих отметки, была непо­стоянна, в газе возникли бы встречные потоки разного рода моле­кул, причем величина потоков определилась бы формулой (5). Для смеси молекул различной массы и сечения соответствующий расчет дает следующее выражение коэффициента диффузии:

Здесь n₁, , λ₁ — концентрация, средняя скорость и средняя длина свободного пробега молекул первого вида, n₂, , λ₂ — те же величины для молекул второго вида.