2.3 Расчёт электрической цепи методом контурных токов

Прежде, чем приступить к рассмотрению примера расчёта схемы методом контурных токов, рассмотрим основные положения этого метода и последовательность расчёта в соответствии с.

Сложные схемы характеризуются наличием значительного числа ветвей. В случае применения предыдущего метода это приводит к необходимости решать систему из значительного числа уравнений. Метод контурных токов позволяет уменьшить число исходных уравнений, а значит несколько облегчить расчёт.

При расчёте методом контурных токов используются понятия не зависимого контура и зависимого контура, которые использовались в предыдущем методе. Кроме них в этом методе используются ещё следующие понятия:

- собственный элемент контура - элемент, относящийся только к одному контуру;

- общий элемент контура - элемент, относящийся к двум и более контурам цепи.

Обозначаем, как и раньше, через К число узлов, а через n число ветвей цепи. Тогда число независимых контуров цепи определяется по уже известной формуле [n-(К-1)].

Метод основывается на предположении, что в каждом не зависимом контуре течёт собственный контурный ток, и вначале находят контурные токи в не зависимых контурах. Токи в ветвях цепи определяют через контурные токи. При этом исходят из того, что в собственных элементах контура токи совпадают с контурным током данного контура, а в общих элементах ток равен алгебраической сумме контурных токов тех контуров, к которым принадлежит данный элемент.

Последовательность расчёта:

1. Определяется число ветвей (n) и число узлов (К) цепи. Находится число независимых контуров [n-(К-1)].

2. Выбирается [n-(К-1)] не зависимых контура.

3. Выбирается условно-положительное направление контурных токов в каждом из независимых контуров (обычно показывается стрелкой).

4. Для каждого из независимых контуров составляется уравнение по второму закону Кирхгофа. При этом падение напряжения на собственных элементах определяется как произведение контурного тока на величину сопротивления, а на общих элементах - как произведение алгебраической суммы всех контурных токов, протекающих через данный элемент, на величину его сопротивления. Обход контура производится, как правило, в направлении собственного контурного тока.

5. Решается система из [n-(К-1)] уравнений и находятся контурные токи.

6. Токи в ветвях схемы находятся следующим образом:

- в собственных элементах контура ток равен контурному току;

- в общих элементах контура ток равен алгебраической сумме токов, протекающих через данный элемент.

Пример применения метода контурных токов при расчёте электрических цепей рассмотрим на той же схеме (рис.3) и представим её на рис.7. Как рассматривалось выше, в этой схеме три независимых контура. Тогда в каждом независимом контуре выбираем направления контурных токов и показываем эти контурные токи.

Вставить контурные токи

Для дальнейшего удобства расчёта расставим в схеме условно-положительные направления токов и напряжений. Далее, в соответствии с п.4 «последовательности расчёта», для каждого независимого контура составляем уравнения по второму закону Кирхгофа. В результате этих действий получаем систему (13) из трёх уравнений:

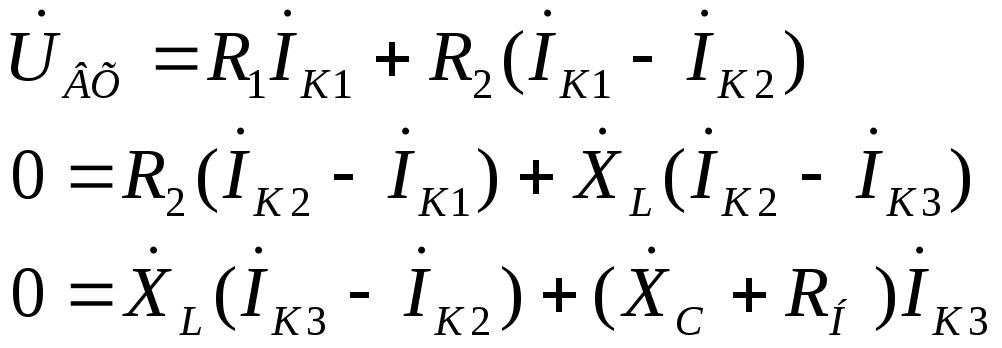(13)

В полученных уравнениях раскрываем скобки и приводим подобные:

(14)

Из третьего уравнения системы (14) находим ток :

(15)

Подставляем выражение тока (15) во второе уравнение системы (14), в результате чего, после приведения подобных членов, эта система принимает вид:

(16)

Во втором уравнении системы (16) коэффициент при токе имеет довольно громоздкий вид. Для дальнейшего анализа будет удобно обозначить его какой-нибудь буквой, например, т.к. этот коэффициент имеет размерность сопротивления:

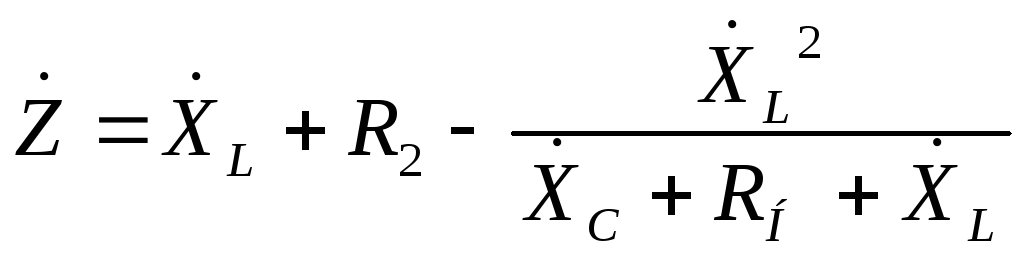. (17)

Подставим численные значения в формулу (17) и найдём значение в алгебраической и показательной форме:

(18)

С учётом (17) система уравнений (16) принимает вид:

(19)

Из второго уравнения системы (19) найдём ток :

. (20)

Подставим выражение для тока (20) в первое уравнение системы (19) и после приведения к общему знаменателю, получим:

.

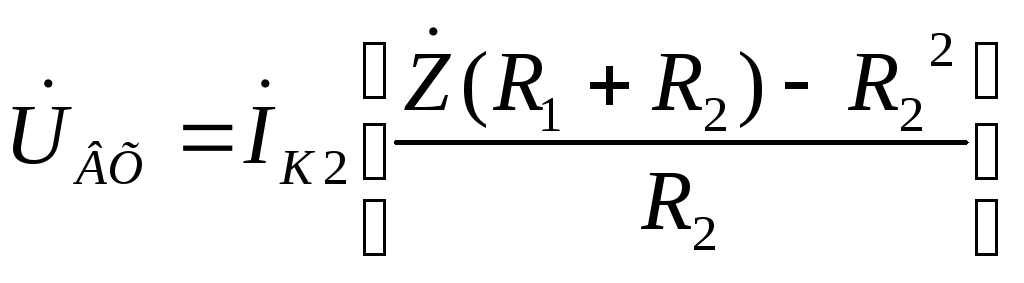Из этого уравнения находим ток :

.

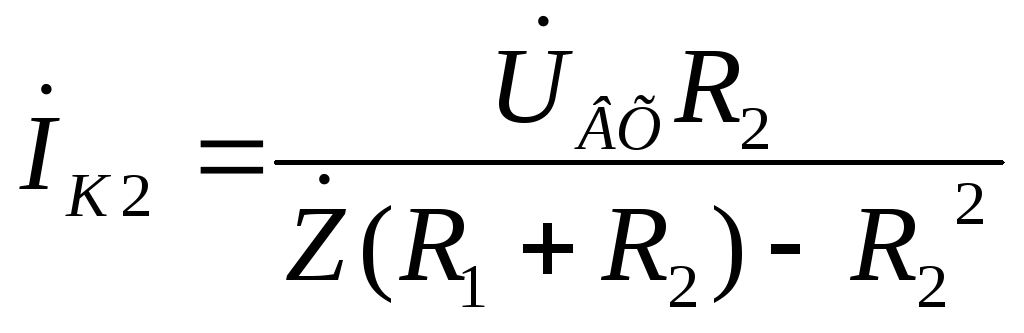В полученное выражение для тока подставляем численные значения и находим значение тока в алгебраической и показательной форме:

. (21)

Для определения тока воспользуемся формулой (20), подставляем в неё численные значения и находим значение тока в алгебраической и показательной форме:

. (22)

Теперь определяем ток , для чего используем формулу (15). Здесь удобнее будет использовать токв показательной форме. Подставляем численные значения в (15) и в результате очевидных преобразований получим значениев показательной форме:

.

В алгебраической форме ток имеет вид:

.

После определения контурных токов переходим к определению токов в ветвях. В соответствии с методом расчёта токи в собственных ветвях контуров равны контурным токам этих контуров. В соответствии с этим находим токи и:

Токи в общих ветвях определяются как алгебраическая сумма контурных токов, протекающих через эти ветви. Ток равен разности контурных токови, так как они протекают через эту ветвь в противоположные стороны:

Подставляем численные значения контурных токов ив алгебраической форме и находим значение токав алгебраической и показательной форме:

Ток равен разности контурных токови, так как они протекают через эту ветвь в противоположные стороны:

Подставляем численные значения контурных токов ив алгебраической форме и находим значение токав алгебраической и показательной форме:

Находим напряжения на элементах:

В.

В.

В.

В.

Определение погрешности расчёта

Определим погрешность выполненного расчёта. В начале определим мощность, выделяемую источником:

Вт.

Далее определим мощность, потребляемую диссипативными элементами схемы по известной формуле:

.

Подставляя численные значения найденных токов, находим:

Вт.

Погрешность определяем по известной формуле:

.

Подставляем найденные значения мощностей:

.

Как видим, точность расчёта этим методом выше точности расчёта предыдущих методов и на порядок выше точности расчёта с помощью законов Кирхгофа. Недостатком этого метода является меньшая наглядность по сравнению с другими методами. Воспользоваться рекомендациями приложения 2 в нём можно только после определения всех токов в ветвях.

Наибольшею наглядностью обладает метод эквивалентного преобразования. В нём видно как формируется полное сопротивление цепи, которое определяет входной ток и как этот ток далее распределяется по ветвям.

Приложение 1

Рекомендации по выполнению расчётно-графической работы.

Практика выполнения РГР показывает, что требуемую точность расчёта не всегда удаётся достичь с первой попытки. В процессе расчётов полезно придерживаться следующих рекомендаций.

1.При эквивалентных преобразованиях цепи необходимо правильно понимать какие элементы включены последовательно, а какие параллельно. Необходимо помнить, что в последовательно соединённых элементах протекает один и тот же ток, а к параллельно соединённым элементам прикладывается одно и тоже напряжение.

2. При переходе от алгебраической формы комплексного числа к показательной его форме следует оценивать с количественной стороны получаемые результаты. Очевидно, что модуль комплексного числа будет больше его мнимой и вещественной составляющей.

Фаза комплексного числа тем больше, чем больше мнимая составляющая превышает вещественную составляющую. Положительное значение мнимой составляющей комплексного числа даёт положительное значение угла, а отрицательное – даёт отрицательный угол.

3. В процессе расчёта полезно контролировать правильность получаемых результатов. Это можно осуществлять путём проверки выполнения законов Кирхгофа в рассчитываемой части цепи. Так после того, как для схемы рис.5 найдены напряжения и , рекомендуется проверить выполнение второго закона Кирхгофа, в соответствии с которым должно выполняться равенство:

.

Проверку выполнения этого равенства можно осуществить как аналитически (по формулам), так и с помощью векторной диаграммы. Последний способ часто оказывается менее трудоёмким.

При расчётах необходимо проверять выполнение известных фазовых соотношений между током и напряжением на элементах схемы. Так на резисторе напряжение и ток должны совпадать по фазе, на конденсаторе ток опережает напряжение на 90⁰, а на индуктивности ток отстаёт от напряжения на 90⁰. Эту проверку можно осуществить и для схемы на рис.5. Здесь на резисторе ток и напряжение должны иметь одинаковые фазы, что в действительности имеет место в расчёте.

Возвращаясь в процессе расчёта к схеме рис.4, после определения токов в ветвях целесообразно проверить выполнение первого закона Кирхгофа, в соответствии с которым должно выполниться следующее соотношение:

.

Проверку выполнения этого равенства удобно выполнить с помощью векторной диаграммы. На векторной диаграмме (рис.6) эта проверка представлена. Здесь же можно проверить и выполнение фазовых соотношений между током и напряжением на резисторе и на катушке индуктивности.

Приложение 2

Рекомендации по построению векторной диаграммы

1. Векторная диаграмма располагается на отдельном листе формата А4.

2. Вектора напряжений и токов строятся на одной векторной диаграмме.

3. На векторной диаграмме обязательно должно присутствовать сетка.

4. Масштабы берутся отдельно для векторов напряжений и для векторов токов.

5. Масштабы должны быть кратными 10-и (0,01; 0,1; 1; 10 и т.д.), 2-м или 5-и.

6. Располагать векторную диаграмму необходимо так, чтобы вектора занимали максимально площадь листа. Так в рассматриваемом примере из результатов расчета по фазовым углам напряжений и токов видно, что вектора будут располагаться в первом и четвертом квадратах, а второй и третий квадраты будут не заняты. Поэтому, как видно на рис.6, векторная диаграмма сдвинута влево, чтобы максимально представить площадь листа для первого и четвертого квадратов.

7. Могут иметь место случаи, когда значения токов или напряжений сильно отличаются по величине, т.е. имеются достаточно большие значения тока и не значительные. Тогда вектор малой величины имеет малый размер и по нему трудно судить о его направлении, в этом случае необходимо сделать вынос этого участка векторной диаграммы на этом же или на отдельном листе. Для этого на основной векторной диаграмме произвольно показывается граница выносимой части, а затем такая же граница показывается на вынесенной части. На вынесенной части берется более крупный масштаб для токов и напряжений. Это приводит к тому, что вектор малых размеров становится различимым и будет видно его фазовое положение относительно других векторов, а остальные вектора будут выходить за границы этой векторной диаграммы. В качестве примера на рис.6 показано как это выполняется относительно тока , хотя в данном примере в этом нет необходимости, т.к. этот вектор хорошо просматривается на основной векторной диаграмме.

Приложение 3

Комплексные величины и действия над ними

При анализе электрических и радиотехнических цепей ши­роко используются комплексные величины. Рассмотрим ос­новные сведения о комплексных величинах.

Комплексное число имеет следующие формы представления: алгебраи­ческую, показательную, геометрическую и тригонометричес­кую.

Алгебраическая форма представления комплексного числа:

, (П.1)

где - вещественная составляющая, - мнимая составляющая комплексного числа.

Комплексное число в показательной форме имеет вид:

, (П.2)

где - модуль комплексного числа,

- фаза комплексного числа.

Комплексное число может быть представлено в виде век­тора на комплексной плоскости (рис.П. 1). Под комплексной плоскостью понимается плоскость, на которой ось абсцисс являет­ся осью вещественных составляющих комплексного числа и обозначается единицей (+1), а ось ординат является осью мнимых составляющих комплексного числа и обозначается . Каквидно из рис.П.1, вектор, соответствующий комплексному числу, характеризуется модулем и фазой, как при показатель­ной форме.

Рис.П.1 Представление комплексного числа на комплексной плоскости

Проекция вектора на вещественную ось комплексной плоскости равна вещественной составляющей комплексного числа в алгеб­раической форме, а проекция этого вектора на мнимую ось равна мнимой составляющей комплексного числа в алгебраи­ческой форме (П.1).

Исходя из векторной диаграммы рис.П.1, вытекает тригонометрическая форма представ­ления комплексного числа:

(П.3)

В процессе расчётов возникает необходимость перехода из одной формы представления комплексного числа в другую. Остановимся на этих действиях. Сравнивая (П.2) и (П.3), можно сделать вывод, что из показательной формы представления комплексного числа (П.2) можно перейти к тригонометрической форме (П.3), выполняя очевидные действия.

Сравнивая формулы (П.1) и (П.3), видно, что:

, . (П.4)

Соотношения (П.4) показывают, что если необходимо перейти из показательной формы представления комплексного числа (П.2) в алгебраическую форму его представления (П.1) необходимо выполнить действия (П.4).

В процессе расчета возникает необходимость суммирования, вычитания, деления и умноже­ния комплексных чисел. Рассмотрим эти действия над комплексными числами.

Очевидно, что два комплексных числа равны, если равны их, соответственно, вещественные и мнимые части при алгебраической форме представления (П.1), или равны их модули и фазы при показательной форме представления (П.2).

Рассмотрим два комплексных числа в алгебраической форме:

, .

Эти же числа в показательной форме (П.2) имеют вид:

, .

Для суммирования или вычитания комплексных чисел их необходимо представить в алгебраической форме. Процесс суммирования (вычитания) состоит в суммировании (вычитании) отдельно вещественных составляющих и отдельно мнимых составляющих комплексных чисел. Тогда сумма (разность) этих чисел будет равна:

. (П.5)

Суммирование и вычитание комплексных чисел можно осуществлять

и в геометрической форме на комплексной плоскости по правилу параллелограмма, т.е. так же, как суммируются вектора (рис. П.2).

Нет векторной диаграммы.

Рис.П.2 Векторное суммирование комплексных чисел

Умножения комплексных чисел.

Рассмотрим вначале умножение комплексного числа на постоянное число.

При умножении комплексного числа на положительное постоянное число изменяется только его модуль. Рассмотрим пример при показательном представлении комплексного числа.

. (П.6)

При умножении комплексного числа на отрицательное число () модуль его изменяется так же, как в предыдущем случае, но так же изменяется и его фаза на.

. (П.7)

При перемножении комплексных чисел они могут быть представлены или в алгебраической форме или в показательной форме. При представлении комплексных чисел в алгебраической форме (П.1) происходит обычное перемножение алгебраических величин с дальнейшей группировкой вещественных и мнимых составляющих. Результаты перемножения имеют вид:

. (П.8)

При представлении комплексных чисел в показательной форме (2) перемножаются их модули, а их фазы суммируются алгебраически, т.е. с учётом знака и результаты перемножения имеют вид:

. (П.9)

Деление комплексных чисел.

При делении комплексного числа на положительное постоянное число изменяется только его модуль. Рассмотрим пример при показательном представлении комплексного числа.

. (П.10)

При делении комплексного числа на отрицательное число () модуль его изменяется так же, как в предыдущем случае, но так же изменяется и его фаза на.

. (П.11)

При делении комплексных чисел они должны быть представлены в показательной форме (П.2). В процессе деления модуль числителя делится на модуль знаменателя, а фаза результирующего числа равна разности фаз числителя и знаменателя:

. (П.12)

Извлечение корня из комплексного числа.

При необходимости извлечения квадратного корня из комплексного числа необходимо подкоренное выражение представить в показательной форме (П.2). В результате извлекается квадратный корень из модуля, а фаза делится на два:

. (П.13)

Умножение и деление комплексного числа на мнимую единицу.

В соответствии с теорией функций комплексного переменного, умножение комплексного числа на мнимую единицу эквивалентно изменению его фазы на. Это значит, что если в комплексном выражении, представленном в показательной форме (П.2), есть мнимая единица в виде сомножителя, то она может быть отброшена, а в место неё фаза изменена на угол.

(П.14)

Деление комплексного числа на мнимую единицу эквивалентно изменению его фазы на . Это значит, что если в комплексном выражении, представленном в показательной форме, есть мнимая единица в виде делителя, то она может быть отброшена, а в место неё фаза изменена на.

. (П.15)

Переход от комплексного числа в виде дроби к комплексному числу в алгебраической форме.

При расчётах часто встречается комплексное выражение в виде дроби

,

которое необходимо представить в алгебраической форме. Решение этой задачи можно выполнить двумя путями. Первый состоит в том, что числитель и знаменатель представляют в показательной форме (П.2), затем выполняется операция деления комплексных чисел (П.12), которая даёт результат в показательной форме (П.2). Для достижения конечного результата необходимо полученное выражение перевести в алгебраическую форму, пользуясь формулами (П.3) и (П.4).

Второй способ состоит в умножении знаменателя и числителя на комплексно-сопряжённое знаменателю число. Знаменатель становится вещественным числом, а в числителе выполняется перемножение комплексных чисел и группировка вещественных и комплексных составляющих. Далее деление вещественной составляющей на знаменатель даёт вещественную составляющую, а деление мнимой составляющей на знаменатель даёт мнимую составляющую комплексного числа.

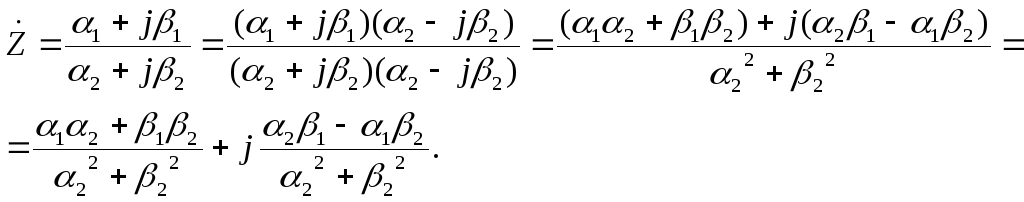
Приложение 4

Оформление Расчётно-графической работы

При выполнении работы необходимо обратить внимание на следующие требования.

Расчётно-графическая работа выполняется на листах формата А4 в соответствии с требованиями к оформлению технической документации РГАТА. Содержание работы может быть выполнено в компьютерном, рукописном или в компьтерно-рукописном вариантах. В последнем случае какая то часть работы может быть выполнена на компьютере, а остальная рукописно. Так, при затруднении с помощью компьютера показать, что число комплексное (точка над ним) или правильно указать его индекс, это можно сделать рукописно.

Последовательность изложения материалов следующая:

-титульный лист (показан ниже);

- содержание расчётно-графической работы – оглавление;

- задание на расчётно-графическую работу;

- исходные данные, содержащие сведения об электрических параметрах элементах схемы и принципиальная схема для расчёта;

- разделы, содержащие анализ и решения в соответствии с требованиями пунктов задания;

- список литературы, используемой при выполнении работы.

Разделы должны быть пронумерованы и должны иметь наименования в соответствии с пунктом задания. В каждом разделе необходимо пояснить суть рассматриваемого в нём вопроса. По поводу выполняемых математических действий необходимо давать пояснения. Принципиальные схемы должны быть выполнены в соответствии с требованиями к начертанию схем. Каждая схема должна быть пронумерована и иметь подпись. Удобной является сквозная нумерация схем, т.е. когда нумерация схемы выполняется последовательно от первой до последней. Формулы, на которые делается ссылка при объяснении, необходимо нумеровать. Нумерацию формул, как и рисунков, удобно делать сквозной.

Федеральное агентство по образованию РЫБИНСКАЯ ГОСУДАРСТВЕННАЯ АВИАЦИОННАЯ ТЕХНОЛОГИЧЕСКАЯ АКАДЕМИЯ имени П.А. СОЛОВЬЕВА
Факультет радиоэлектроники и информатики
Кафедра радиоэлектронных и телекоммуникационных систем (РТС) Специальность 210201 Проектирования и технология РЭС
РЕКОМЕНДАЦИИ ПО ВЫПОЛНЕНИЮ
по дисциплине “Общая электротехника и электроника”
на тему
ИССЛЕДОВАНИЕ ЦЕПЕЙ ВТОРОГО ПОРЯДКА
Исполнитель, студент группы		Вадим
Работа сдана “___” ________ 201 г.
Руководитель, канд. техн. наук, доцент		Станевко В.Н.
Оценка “___” ________ 201 г.
Рыбинск 201 г.

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1. Станевко В. Н. Основы теории цепей: Учебное пособие. Часть 1. – Рыбинск, РГАТА имени П. А. Соловьёва, 2009 – 172 с.

2.Атабеков Г. И. Основы теории цепей: Учебник для вузов. – М.: Энергия,1969. – 424с.

3.Араманович И.Г., Лунц Г. Л., Эльсгольц Л. Э. Функции комплексного переменного, операционное исчисление, теория устойчивости: Учебное пособие для вузов. – М.: Наука, 1985. – 392 с.