7.9. Идеально упругое тело. Упругие напряжения и деформации. Закон Гука. Модуль Юнга. Энергия упругих деформаций твердого тела
Всякое
реальное тело под действием приложенных
к нему сил деформируется, т.е.изменяет
свои размеры и форму. Если после
прекращения действия сил тело принимает
первоначальные размеры и форму,
деформация называется упругой. Упругие
деформации наблюдаются в том случае,
если сила, обусловившая деформацию, не
превосходит некоторый предел, называемый
пределом упругости.
Если после прекращения действия сил форма и размеры тела не восстанавливаются, говорят о неупругой деформации.
Рассмотрим
пружину, имеющую в недеформированном
состоянии длину
,
и приложим к ее концам равные по величине,
противоположно направленные силы
и
(рис.7.19). Под действием этих сил пружина
растянется на некоторую величину
,
после чего наступит равновесие. В
состоянии равновесия внешние силы
и
будут уравновешены упругими силами,
возникшими в пружине в результате
деформации. При небольших деформациях
удлинение пружины
оказывается пропорциональным
растягивающей силе:
(7.7)
-
это закон Гука. Здесь
-
коэффициент жесткости пружины.
Упругие
натяжения возникают во всей пружине.
Любая часть пружины действует на другую
часть с силой, определяемой формулой
(7.7). Поэтому, если разрезать пружину
пополам, та же по величине упругая сила
будет возникать в каждой из половин
при в два раза меньшем удлинении. Таким
образом, при заданных материале пружины
и размерах витка величина упругой силы
определяется не абсолютным удлинением
пружины
,
а относительным удлинением
При
сжатии пружины также возникают упругие
натяжения, но другого знака. Обобщим
формулу (7.7) следующим образом. Закрепим
один конец пружины неподвижно (рис.7.20),
а удлинение пружины будем рассматривать
как координату
другого конца, отсчитываемую от его
положения, отвечающего недеформированной
пружине. ПодF
будем понимать проекцию на ось X
упругой
силы
.
Тогда можно записать:
.
(7.8)
Из рис.7.20 видно, что проекция упругой силы на ось X и координата x всегда имеют разные знаки.
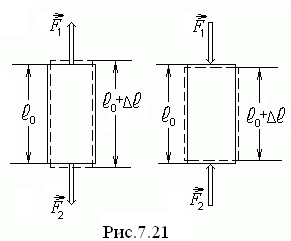
Однородные
стержни ведут себя при растяжении или
одностороннем сжатии подобно пружине.
Если к концам стержня приложить
направленные вдоль его оси силы
и
,
действие которых равномерно распределено
по всему сечению, то длина стержня
получит положительное ( при растяжении)
или отрицательное (при сжатии) приращение
(рис.7.21).Деформация стержня характеризуется
относительным изменением длины:
Экспериментально доказано, что для стержней из данного материала относительное удлинение при упругой деформации пропорционально силе, приходящейся на единицу площади поперечного сечения стержня:
.
(7.9)
Коэффициент пропорциональности называется коэффициентом упругой податливости.
Величина,
равная отношению силы к площади
поверхности, на которую действует сила,
называется напряжением. В результате
взаимодействия частей тела друг с
другом напряжение передается во все
точки тела и весь объем стержня
оказывается в напряженном состоянии.
Если сила направлена по нормали к
поверхности, напряжение называется
нормальным и обозначается .
Если сила направлена по касательной к
поверхности, возникает тангенциальное
напряжение
.
В
выражении (7.9)
,
поэтому
.
Величина,
обратная упругой податливости, называется
модулем Юнга
С учетом сказанного,
.
Модуль Юнга равен такому нормальному
напряжению, при котором относительное
удлинение было бы равно единице.
Решив
записанные уравнения относительно F
получаем:
.
Это закон Гука для стержня.
Рассмотрим
энергию упруго деформированного тела.
Для этого в сплошной упругой среде
выделим элементарный объем
настолько малый, что скорости движения
и деформации во всех его точках одинаковы.
Выделенный объем обладает кинетической
энергией
где
- масса объема,
- его скорость. Разделив эту энергию на
величину объема, получим объемную
плотность кинетической энергии
(7.10)
Рассматриваемый
элемент объема обладает потенциальной
энергией упругой деформации. Чтобы
найти эту энергию, представим выделенный
объем в виде стержня с площадью
поперечного сечения S
и длиной
.
Один конец стержня закреплен, ко второму
приложим растягивающую силу
и будем медленно увеличивать ее от 0
до
.
Удлинение стержня будет при этом
меняться от 0 до х. По закону Гука
где
- коэффициент упругости. Работа силы
упругости в этом процессе
Эта
работа идет на увеличение упругой
энергии U
. т.е.
Плотность этой энергии
(2.10)
где
- напряжение, Е
– модуль Юнга,
- относительная деформация,
,
и объемная плотность потенциальной
энергии равна
Объемная
плотность полной энергии среды равна