книги / Труды IX Международной (XX Всероссийской) конференции по автоматизированному электроприводу АЭП-2016 , Пермь, 3-7 октября 2016 г

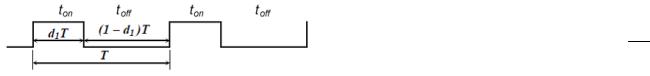
Дифференциальные уравнения, описывающие поведение ККМ, для замкнутого состояния ключа S представлены системой (1), для разомкнутого – системой (2).

L

di

L

= vin .

dt

(1)

dvout

−vout

=

.

C

dt

L

R

L

di

L

= vin

− vout ,

dt

(2)

dvout

= iL

−

vout

C

.

dt

R

L

Система уравнений (1) существует в течение интер-

вала времени d1 T, система (2) – в течение интервала

(1 – d1) T, где d1 = ton/T (рис. 3).

Рис. 3. Временная диаграмма работы транзистора ККМ

Усредненная система дифференциальных уравнений получается умножением систем (1) и (2) на d1 и (1 – d1) соответственно, и с последующим суммированием:

L		diL		= vin − (1− D1 )vout		+ Vout d1 ,
		dt
									(6)
C		dvout			= (1− D1 )iL − d1	IL −	vout	.
		dt					RL

Приведем систему (6) к операторным уравнениям:

Lsi = v

in

− (1− D )v

out

+ V

d

,

L

1

out

1

vout

(7)

Csv

= (1− D )i

− d

I

−

.

L

out

1

L

1

RL

Из (5) и (7) выразим передаточную функцию для контура тока:

	=	i	=	V	(2 + R Cs)		.	(8)
G		L		out	L
		d1		LRLCs2 + Ls + (1− D1 )2
id						RL

Для того чтобы найти передаточную функцию кон-

v

тура напряжения, необходимо найти отношение out , vc

где vc является выходом регулятора напряжения.

На основании структурной схемы, представленной на рис. 2, а, выражение для заданного тока можно представить следующим образом:

iref = iL = iin = k Vin Vc ,

(9)

di

= vin

− vout (1− d1 ),

где Vin –

напряжение сети;

Vc –

выход регулятора на-

L

L

dt

(3)

k f km

dv

v

пряжения; k =

.

(1− d1 ) −

2

C

out

= iL

out

.

Vin _ rms

dt

R

Представим мгновенные значения переменных (9)

L

Представим мгновенные значения переменных со-

в виде суммы стационарной составляющей (Iin, Vin, Vc)

и малого

возмущения

от

стационарного

режима

стояния и воздействий в виде суммы стационарной со-

( i , v

, v

).

ставляющей (IL,

Vout, VIN, D1)

и малого возмущения от

in

in

c

стационарного режима ( i , v

out

, v

in

, d ).

iin + Iin = k (Vin + vin )

(Vc

+ vc ) .

(10)

L

1

dIL

diL

L

+ L

= Vin + vin

− (Vout + vout ) (1− D1 − d1 ),

В результате уравнение (10) разделится на две час-

dt

dt

(4)

ти: уравнение для стационарных значений и уравнение

dVout

dvout

для малых возмущений переменных относительно ста-

C

+ C

= (IL + iL ) (1− D1 − d1 )−

(Vout + vout

)

.

ционарных значений (11):

dt

dt

RL

i = k v

v

+ k v

v

in

c

in

V

+ k V

c

.

(11)

В результате мы получаем две отдельные системы

in

c

in

уравнений: первая – для стационарных значений пере-

Пренебрегаем произведениями малых возмущений,

менных (5), и вторая – для малых возмущений пере-

и тогда уравнение примет окончательный вид

менных относительно стационарных значений (6):

Vc

(12)

Vin = (1− D1 )Vout ,

iin

= k vin

+ k Vin vc .

(5)

V

=

(1− D1 ) IL .

При выводе передаточной функции контура напря-

out

RL

жения примем следующее допущение:

входная мощ-

____________________________________________________________________________________________________________________________

IX Международная (XX Всероссийская) конференция по автоматизированному электроприводу АЭП-2016

- 221 -

ность за период коммутации равна выходной мощности

[3], т.е.

iin Vin = iout Vout .

(13)

Учитывая (9), преобразуем (13):

kV	2V	= i	V .	(14)
in	c	out	out

Представим мгновенные значения переменных (14) в виде суммы стационарной составляющей (Iin, Vin, Vc) и малого возмущения от стационарного режима

( iin , vin , vc ):

k (vin +Vin )2 (vc +Vc ) = (iout + Iout )(vout +Vout ). (15)

Уравнение (15) можно разделить на две части: уравнение для стационарных значений и уравнение для малых возмущений переменных относительно стационарных значений. Вторая часть с учетом пренебрежения произведения малых возмущений представлена далее:

2				Iout .	(16)
kvcVin	+ 2kVinVc vin	= iout Vout	+ vout

Из (16) определим iout :

i

=

2kVinVc

v

+

kVin

2

v

c

+

Iout

v

out

.

(17)

in

out

Vout

Vout

Vout

Введем понятие малосигнального сопротивления

rout = Vout , а также коэффициент конверсии устойчиво-

Iout

го состояния M = Vout [3]. Представим (14) следующим

Vin

образом:

kV	2V	=		iout	V	2 =	1	V	2 .	(18)
in	c				out			out
			Vout				rout

Тогда коэффициент M можно представить еще следующим образом:

M =	Vout	= r	kV .	(19)
		out	c
	Vin

Также отдельно стоит представить еще один вариант:

kV =

M 2

.

(20)

c

rout

Учитывая вышеописанные преобразования, формулы (12) и (17) можно представить следующим образом:

= kV

+

M 2

,

(21)

i

in

v

c

v

in

in

rout

=

2M

+

kVin

+

1

iout

vin

vc

vout .

(22)

M

rout

rout

На основании формул (21) и (22) можно построить малосигнальную модель ККМ, которая представлена на рис. 4.

rin

C

ZL

gi vc

g f vin

gc vc

r

v

out

in

vout

Рис. 4. Малосигнальная модель ККМ

Здесь rin =

M 2 , g = kV , g =

2M

, g

=

kVin

.

c

i

in

f

rout

M

rout

vout

Поскольку

нас интересует именно

соотношение

, то схему на рис.

4 можно упростить до вида на

vc

рис. 5.

g vc

r

C

ZL

vout

c

out

Рис. 5. К определению передаточной функции контура напряжения

Таким образом, передаточная функция контура напряжения имеет вид

rout

1

r

Z

Cs

L

vout

= g

= g

out

.

(23)

v

c

+

1

c 1

+ Csr

Z

c

rout

out

L

Cs

Импеданс нагрузки может быть представлен разными вариантами. В [4] указано, что если ККМ подключен к последующему преобразователю, то данный вариант считается нагрузкой с постоянной потребляемой мощностью и входное сопротивление последующего преобразователя считается равным выходному сопротивлению ККМ. Передаточная функция контура напряжения в этом случае представлена формулой

G	=	vout	= g		1	.	(24)
vc		vc		c Cs

____________________________________________________________________________________________________________________________

IX Международная (XX Всероссийская) конференция по автоматизированному электроприводу АЭП-2016

- 222 -

II. СИНТЕЗ СИСТЕМЫ УПРАВЛЕНИЯ

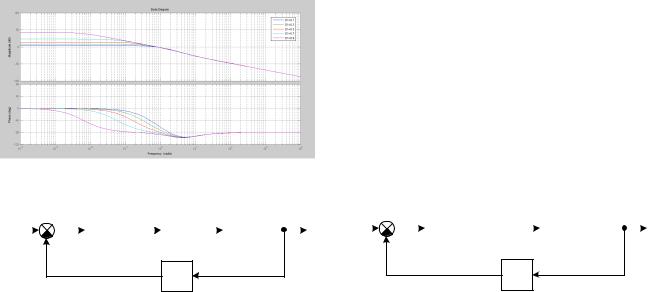
Передаточная функция контура тока представлена выражением (8). ЛАЧХ и ЛФЧХ этой передаточной функции для разных значений D1 приведены на рис. 6.

Видно, что при частотах выше 500 Гц все ЛАЧХ и ЛФЧХ сводятся к одной. Поскольку контур тока работает на частотах выше 1 кГц, то справедливо заменить передаточную функцию контура тока (8) на аппроксимированную:

				i		V
			G (s) =	L	=		out	.	(25)
				d
			id				Ls
				1
	Структурнаясхемаконтуратокапредставленанарис. 7.
	Здесь Gid (s)		– передаточная функция контура тока;
	GCEA (s) – передаточная функция регулятора								контура
	тока; ks =	1	– коэффициент обратной связи; Fm –
		IL _ max

функция модуляции. Примем Fm = 1 . Тогда передаточная функция разомкнутой системы имеет вид

H (s) = G

(s) G

(s) k

= G

(s)

ksVout

.

(26)

s

CEA

id

CEA

Ls

Передаточная функция регулятора

G

(s)

= K

+

Ki

.

(27)

p

CEA

s

Тогда

K

p

=

L 2πfci

,

(28)

ksVout

Рис. 6. ЛАЧХ и ЛФЧХ передаточной функции контура тока

iref

GCEA

(s)

Fm

Gid (s)

iL

ks

Рис. 7. Структурная схема контура тока

где fci – частота полосы пропускания контура тока.

В соответствии с [5] частота полосы пропускания выбирается в диапазоне 8–10 кГц.

K		=	K p 2πfzi	,	(29)
	i
			fsi

где fzi – частота компенсации нулей; fsi – частота рас-

чета контура тока. В соответствии с [5] частота компенсации нулей выбирается в 3–10 раз меньше, чем fci .

Передаточная функция контура напряжения представлена в (24), раскроем эту формулу, подставив коэффициенты:

(s) =

v

out

=

k f

km

V

2

1

,

(30)

G

in

v

V

V

Cs

VEA

c

2

in

_ rms

out

где k f =

1

,

km =

Vout _ max

.

Vin _ max

Vin _ min

Причем стоит указать, что под Vin _ rms2 понимается не

среднеквадратичное значение входного напряжения, взятое в квадрате, а это же значение, но с учетом коэф-

фициента kf, т.е. (RMS (Vin k f ))2 . Положим, что питающее напряжение содержит только 1-ю гармонику с ам-

	плитудой 310 В, тогда	2				1	2
		Vin _ rms	= RMS		310			= 2.
						310

Окончательный вид передаточной функции контура напряжения принимает вид

					k		k V		2
G	(s) =	vout		=		f	m	in		.	(31)
VEA					2V			Cs
		v	c
							out

Контур тока считаем скомпенсированным. Структурная схема контура напряжения представлена на рис. 8.

Здесь Gvc (s) – передаточная функция контура напряжения, GVEA (s) – передаточная функция регулятора

	контура напряжения; kd =	1	– коэффициент об-
		Vout _ max

ратной связи. Тогда передаточная функция разомкнутой системы имеет вид:

k

k

k V

2

H (s) = G

(s) G

(s) k

= G

(s)

f

d

m in

. (32)

d

VEA

vc

VEA

2Vout Cs

Vref

Vout

GVEA (s)

Gvc (s)

kd

Рис. 8. Структурная схема контура напряжения

____________________________________________________________________________________________________________________________

IX Международная (XX Всероссийская) конференция по автоматизированному электроприводу АЭП-2016

- 223 -

Передаточная функция регулятора

G

(s)

= K

+

Ki

.

(33)

p

VEA

s

Тогда

K

=

2Vout C 2πfcv

,

(34)

p

k

f

k

k V

2

d

m in

где fcv – частота полосы пропускания контура напря-

жения. В соответствии с [5] частота полосы пропускания выбирается в диапазоне 10–20 Гц.

	K		=	Ki 2πfzv	,	(35)
		i		fsv
	где fzv – частота компенсации				нулей;	fsv – частота
	расчета контура напряжения.

III. МОДЕЛИРОВАНИЕ

Исходные данные: мощность P = 250 Вт, входное на-

пряжение Vin = 310 В, выходное напряжение Vout = 400 В,

Vin_max = 410 В, Vin_min = 80 В, Vout_max = 410 В. Частота

коммутации fsw = 100 кГц. Частота расчета fsi = fsv = 50 кГц,

L = 0,001 Гн, C = 500 мкФ, IL_max = 5,5 A. Полоса пропуска-

нияконтуранапряженияfcv = 10 Гц, контуратокаfci = 8 кГц. Параметры ПИ-регулятора контура тока

L 2πfci

1 10−3

2π 8

103

K

p

=

=

5,5 400

= 0,691 .

(36)

ksVout

1

K p 2πfzi

0.691

2π 1 103

K

i

=

=

50 103

= 0,087 .

(37)

f

si

Параметры ПИ-регулятора контура напряжения

K

=

2Vout C 2πfcv

=

2

400 500 10−6 2π 10

= 6,5

(38)

p

k f kd kmVin

2

1

1

410

2

310

410

80

310

K

=

K p

2πfzv

=

6.5 2π 10

= 0,008.

(39)

i

f

sv

50 103

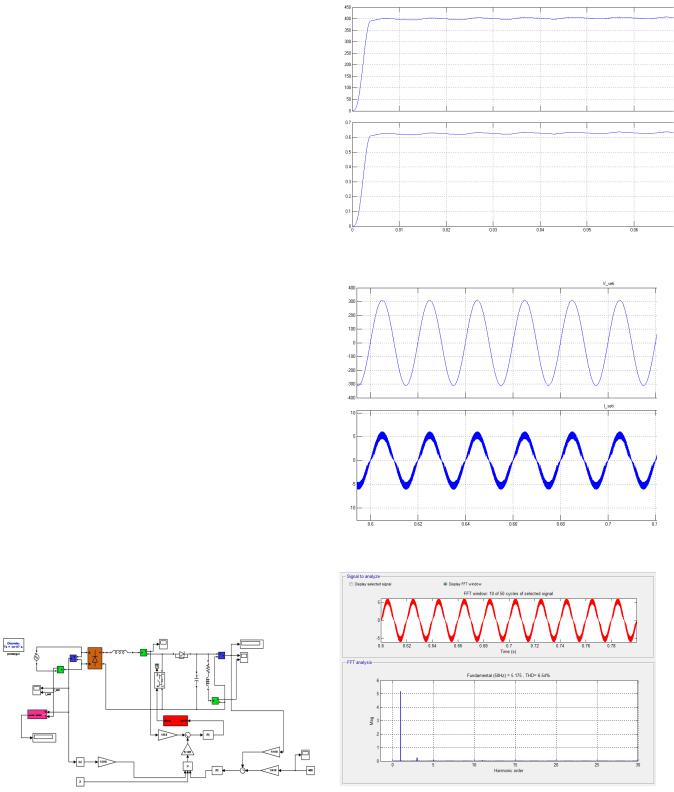
Модель ККМ выполнена в Simulink с применением элементов SymPower и представлена на рис. 9.

Результаты моделирования представлены далее

(рис. 10–12).

Рис. 10. Напряжение и ток нагрузки

Рис. 11. Напряжение и ток сети в установившемся режиме

Рис. 9. Модель ККМ

Рис. 12. Гармонический анализ потребляемого из сети тока

____________________________________________________________________________________________________________________________

IX Международная (XX Всероссийская) конференция по автоматизированному электроприводу АЭП-2016

- 224 -

ЗАКЛЮЧЕНИЕ

Обеспечение энергоэффективной работы технологического оборудования достигается путем использованием энергосберегающих систем автоматизированного электропривода. Одним из вариантов построения таких систем является применение асинхронного электропривода с ККМ.

Встатье был проведен анализ ККМ, построенного на базе повышающего преобразователя напряжения. Данный ККМ имеет внутренний контур тока и внешний контур напряжения. Проведенный анализ был основан на применении метода усреднения пространства состояний. В результате были получены передаточные функции для обоих контуров. Также для каждого контура был синтезирован регулятор.

Всистеме инженерных расчетов MatLab Simulink

выполнено функциональное моделирование ККМ с заданными параметрами. На представленных результатах видна работоспособность моделируемой системы: напряжение на выходе ККМ стабильно и соответствует заданному, потребляемый из сети ток синфазен напряжению, форма близка к синусоиде. Также был проведен

гармонический анализ потребляемого из сети тока, его результаты представлены на рис. 12.

Благодарности

Исследование выполнено за счет гранта Российского научного фонда (проект № 14-19-00972).

Библиографический список

1.IEC 61000-3-2: 1995 Edition 1 Electromagnetic compatibility (EMC) – Part 3: Limits - Section 2: Limits for harmonic current emissions (equipment input current < = 16 A per phase).

2.ГОСТ 13109-97. Электрическая энергия. Совместимость технических средств электромагнитная. Нормы качества электрической энергии в системах электроснабжения общего назначения. М.: Станадартинформ, 2006.

3.Ridley R.B. Average small-signal analysis of the boost power factor correction circuit // Proceedings of the Virginia Power Electronics Center Seminar (VPEC). Blacksburg, Virginia. P. 108–120.

4.Larsson C., Johansson O. Active Power Factor Correction for Airborne Applications // Master of Science Thesis, Department of Energy and environment Division of Electric Power Engineering, CHALMERS UNIVERSITY OF TECHNOLOGY. Gothenburg, Sweden, 2012.

5.Xie M. Digital Control For Power Factor Correction scholar.lib.vt. edu/theses/available/etd-07302003-111145/unrestricted/Finalthesis.pdf

____________________________________________________________________________________________________________________________

IX Международная (XX Всероссийская) конференция по автоматизированному электроприводу АЭП-2016

- 225 -

УДК 681.513.5

Синтез программного движения на основе оптимального, включая особое, управления

В.С. Хорошавин

Вятский государственный университет, Киров, Россия

Software synthesis based on optimal movement, including special control

V.S. Khoroshavin

Vyatka State University,

Kirov, Russian Federation

Предлагается способ синтеза систем программного движения на основе решения оптимальной задачи с интегральным функционалом на минимум отклонения координат от заданного движения под кусочно-постоянным управлением, получаемым из принципа максимума в задачах с линейным вхождением управления, и под особым управлением, вычисляемым с помощью условий общности положения для нелинейных объектов.

A method of synthesis of systems software movement based on the decision of the optimum task with integral functionality to a minimum deviation from the specified coordinates movement under the piecewise-constant control, derived from the principle of maximum in problems with linear entry control, and under special control, conditions of the commonality of the provisions for nonlinear objects.

Ключевые слова: синтез замкнутых систем программного движения, интегральный функционал, принцип максимума; условияобщностиположениядлянелинейныхобъектов.

Keywords: synthesis closed systems motion software, integrated functionality, maximum principle, terms of communion of the situation for nonlinear objects.

ВВЕДЕНИЕ

В задаче синтеза программного движения для обеспечения наперед заданной в функции времени траектории движения (обычно конечной координаты) под управлением в замкнутой системе (управлением в функции координат) многие авторы (например, А.А. Колесников [1]) указывают на три группы методов решения:

♦ инженерный метод формирования переходного процесса с заданием показателей качества (времени первого согласования, колебательности, перегулирования, времени переходного процесса и других) на основе логарифмических амплитудных и фазовых частотных характеристик В. В. Солодовникова;

♦аналитический, когда при известных в функции времени траекториях объекта, известной структуре и звеньях системы путем обратного решения с выхода на вход находятся координаты и управления в функции времени, а после исключения времени формируется управление в функции координат. К этой группе можно отнести работу Л. М. Бойчука [2], который назвал его методом «структурного синтеза»;

♦интегральный метод решения оптимальной задачи на минимум ресурсов с подинтегральной функцией, учитывающей ресурсы системы по координатам и управлению (метод аналитического конструирования регуляторов А. А. Фельдбаума, А. М. Летова, Калмана; функционала обобщенной работы А. А. Красовского, упреждающего функционала А. А. Колесникова).

Известные методы синтеза применимы в основном для линейных объектов, причем требуют многократного последовательного применения для получения конечного результата, а метод Л. М. Бойчука к тому же требует знания высших производных выходного сигнала.

В данной работе предлагается способ решения задачи синтеза систем программного движения на основе решения с помощью принципа максимума Л. С. Понтрягина

[3]оптимальной задачи с интегральным функционалом на минимум отклонения координат от заданного движения под кусочно-постоянным управлением, получаемым из принципа максимума в задачах с линейным вхождением управления, и под особым (в смысле принципа максимума) управлением, вычисляемым с помощью аппарата условий общности положения (УОП) для нелинейных объектов [4, 5]. Предлагаемый способ по форме входит в группу интегральных методов, но по содержанию близок к группе аналитических методов, а в целом отражает синергетический подход к синтезу систем управления [6].

____________________________________________________________________________________________________________________________

IX Международная (XX Всероссийская) конференция по автоматизированному электроприводу АЭП-2016

- 226 -

I.ПРЕДЛАГАЕМОЕ РЕШЕНИЕ

Вобщем виде исходную задачу синтеза программных движений как заданных функций координат от времени можно рассматривать как нестационарную задачу

впространстве координат объекта размерности Rn

x = A(x,t ) + B (x,t )U ,

J = t	p(x,t )dt.	(1)
0

Классиками принципа максимума [3] для нахождения оптимального управления исходная задача решается в расширенном пространстве координат размерности Rn+2 с дополнительными переменными, учитывающими функционал и явное вхождение времени:

x0 = p (x, xn+1 ),

xn+1 = 1.

Для расширенной системы в Rn+2 с использованием УОП для нелинейных объектов вычисляются векторы

Bj (j = 2, …, n + 2),

		0
B =	B (x, x		n+1	)	,
1
		0

по рекуррентному соотношению

∂B

j −1

∂

A(x)

B (x)U

∂B

j −1

Bj =

dU −

+

∂

Bj −1

+

dx . (2)

∂x

∂x

∂U dt

∂x dt

Образовав матрицу Dn+2

размером ((n + 2) × (n + 2))

из векторов

(B1 … Bn+2) и

вычислив ее

определитель

det Dn+2 = 0, находим уравнения особых траекторий и особых управлений.

Данная процедура введения особых ситуаций в нестационарных задачах исследована автором в [5]. Можно согласиться с тезисом о неединственности оптимального управления из-за тождества det Dn+2 = 0, так как ввиду повторяемости процессов для разных начальных условий получаем одинаковые значения функционала. Но выдвигаемый далее в [5] тезис о невклю-

чении времени	как координаты (т.е. невключении
xn+1 = t , xn+1 = 1)	является спорным. В работах [7, 8]

справедливость последнего тезиса подтверждена практическими примерами с дрейфом экстремальной статической характеристики, учитывающим возмущения на объект. Если же проводить синтез управления, то невключение времени в уравнения движения может вести к потере свойств управления из-за потери зависимости матриц A и B от времени.

И еще одно дополнение к УОП для нестационарных объектов [5]. Оно касается конструктивности результатов, точнее их нетривиальности, связанной с тем, что если взять в функционале точное равенство (xзадан(t) = x(t)),

то можем прийти, например, к ситуации задачи Эйлера– Лагранжа (x1 + x2) → min с ограничением x12 + x22 = 0 , для нетривиальности результатов в которой ограничения задаются окрестностью x12 + x22 = ε, в рассматриваемой задаче необходимо знать области притяжения

xзадан (t ) − x (t ) ≤ ε .

Полученное с помощью УОП особое управление дополняется кусочно-постоянным оптимальным управлением, полученным из условий принципа максимума в задаче (1). Необходимость и условия стыковки не особых и особых траекторий зависят от граничных условий и точности реализации программного движения.

II.ПРИМЕР ИСПОЛЬЗОВАНИЯ

Вкачестве примера использования предлагаемого подхода рассмотрим пример, взятый из [2, с. 39], о синтезе автоколебательной системы для одного интегратора:

x1 = U a0

с требуемым выходным сигналом

x1 = Asin ωt .

В расширенном пространстве координат Rn+2 = R3 запишем поставленную задачу

x0 = ( Asin ωx2 − x1 )2 ,

x1	=	U	,	(3)
		a0

x2 = 1.

Выделяя элементы матриц А (x) и B (x) для матричной формы записи последних уравнений в виде

x = A(x) + B (x)U , последовательно вычисляя векторы Bj, j = 2, 3 по соотношению (2), образуем матрицу

			2		( Asin ωx2	− x1 )	−	2U		+	2
		0										Acos ωx2	ω
				a				a	2		a
									0
			0								0
D3	=	1			0							0	.
	a0
		0			0							0
Проанализируем det D3:
	det D3		≡ 0 , что говорит о неединственности процес-

сов управления из-за их повторяемости в любые начальные моменты времени;

det D2/ d		=	1		−	2U	+	2	Acos ωx2	ω = 0 , что дает
	32		a0			a02 a0

решение a0 = ∞, ведущее к неуправляемости процесса, и решение для особого управления:

____________________________________________________________________________________________________________________________

IX Международная (XX Всероссийская) конференция по автоматизированному электроприводу АЭП-2016

- 227 -

	U = a0 A ω cos ωx2 ,					(4)
	det D2/ d		= −	2	( Asin ωx2 − x1 ) = 0 .	(5)
		33		a2
			0

Совместное решение уравнения особого управления

(4) и особой траектории (5) дает управление автоколебательным процессом объекта в функции выходной координаты

U	oc	= a ω	A2 − x2	,	(6)
		0	1

что совпадает с полученным в [2].

Далее, если перейти к структуре замкнутой системы управления, то в методе структурного синтеза Бойчука [2] указывается на трудности запуска режима автоколебаний для объектов с одним и двумя интеграторами [2, с. 39, 40, 69–71], что ведет к «застреванию» системы при скорости изменения выходной координаты, близкой к нулю. Там же предлагаются схемные решения для исключения застревания, которые, может быть, являются новыми техническими решениями, но полученными эвристическим путем.

Предлагается пойти формализованным путем, используя решение задачи оптимального управления для рассматриваемой системы (3) с одним интегратором в расширенном пространстве R3. Тогда на основе принципа максимума и УОП получим, что оптимальное управление состоит из участков не особого релейного управления Uрел = –Umax · sing x1 и особого непрерывного управления (6). Реализация предлагаемого алгоритма управления не вызывает затруднений в аппаратном или программном варианте.

III. ВЫВОДЫ

Приведенный простейший пример имел целью показать методику предлагаемого подхода к задаче синтеза программного движения, его достоверность, формализованность и эффективность. Что касается автоколебательных режимов, то это в настоящее время вылилось в новую теорию аналитического конструирования

агрегированных регуляторов колебаний – АКАРК [8], одним из подходов к ее решению может быть предлагаемый. Можно указать и другие области применения – это задачи модального и прямого адаптивного управлений.

Еще одна область применения предлагаемого подхода – это системы координационного или согласованного управления координатами [9]. На наш взгляд, интерес представляет справедливое утверждение авторов [9], что в последнее двадцатилетие «…совершенствование автоматических систем базировалось на развитии технических средств автоматики, основанное на достижениях в области электроники, приборостроения, вычислительной техники и мехатроники, а теоретическая база систем автоматического управления слабо развивалась». Таким образом, можно говорить об актуальности и важности развития предлагаемого подхода.

Библиографический список

1.Колесников А.А. Последовательная оптимизация нелинейных агрегированных систем управления. М.: Энергоатомиздат, 1987. 160 с.

2.Бойчук Л.М. Метод структурного синтеза нелинейных систем автоматического управления. М.: Энергия, 1971. 112 с.

3.Математическая теория оптимальных процессов / Л.С. Понтрягин, В.Г. Болтянский, Р.В. Гамкрелидзе, Е.Ф. Мищенко. М.:

Наука, 1976.

4.Олейников В.А. Оптимальное управление процессами в нефтяной и газовой промышленности. Л.: Недра, 1982. 216 с.

5.Хорошавин В.С. Прикладные методы качественного исследования особых управлений и структур нелинейных оптимальных систем: дис. … д-ра техн. наук: 05.13.01; Киров. политехн. ин-т.

Киров, 1993. 402 с.

6.Колесников А.А. Синергетическая теория управления. М.: Энергоатомиздат, 1994. 344 с.

7.Экстремальное управление нестационарными нелинейными объектами при вертикальном дрейфе статической характеристики с аддитивным вхождением времени в математическое описание /

В.С. Хорошавин, А.В. Зотов, С.И. Охапкин, В.С. Грудинин // Современные проблемы науки и образования. 2014. № 2.

8.Колесников А.А. Метод синергетического управления самоорганизующимися нелинейными колебательными системами // Известия ЮФУ. Технические науки. 2015. № 5 (166). С. 231–242.

9.Филимонов А.Б., Филимонов Н.Б. О проблематике синтеза координирующих систем автоматического управления // Изв. ЮФУ.

Технические науки. 2012. № 3 (128). С. 172–180.

____________________________________________________________________________________________________________________________

IX Международная (XX Всероссийская) конференция по автоматизированному электроприводу АЭП-2016

- 228 -

УДК 621.316.718.5

Адаптивный регулятор частоты вращения электродвигателя

С.В. Шарашкин, В.Ф. Самосейко

Государственный университет морского и речного флота имени адмирала С.О. Макарова, Санкт-Петербург, Россия

The adaptive controller of motor speed

S.V. Sharashkin, V.F. Samoseyko

Admiral Makarov State University of Maritime and Inland Shipping,

St. Petersburg, Russian Federation

Описан адаптивный регулятор частоты вращения электродвигателя. Показаны его преимущества над другими видами регуляторов, применяющихся при построении подчиненных систем управления электроприводом.

The article discusses the adaptive controller of motor speed. The advantages of the adaptive controller over other types of controllers that are used synthesis subordinate drive control systems.

Ключевые слова: адаптивный регулятор, подчиненная система управления.

Keywords: adaptive controller, subordinate control systems.

ВВЕДЕНИЕ

Современные автоматизированные электроприводы в большинстве случаев имеют подчиненную систему управления, при построении которой для ограничения тока в двигателе используют нелинейные ограничители. Подчиненную систему управления невозможно составить без использования регуляторов, в частности пропорционально-интегральных (ПИрегуляторы), пропорционально-дифференциальных (ПД-регуляторы), пропорционально-интегрально- дифференциальных (ПИД-регуляторы) регуляторов. Существует множество реализаций регуляторов, рассмотрим некоторые из них.

I. ВИДЫ РЕГУЛЯТОРОВ

щается процесс интегрирования. Кроме того, когда выходной сигнал регулятора достигает одного из пределов ограничения, предотвращается дальнейшие увеличение выходного сигнала дифференциатора. В этом случае выходной сигнал дифференциатора, являющийся составной частью выходного сигнала регулятора и вызывающий срабатывание схемы ограничения интегрирования, приводит к нежелательному изменению интегральной составляющей. Это явление приводит к значительному ухудшению качества регулирования.

Известны также регуляторы, содержащие усилители, интеграторы, дифференциаторы, сумматоры, релейные и нелинейные элементы, например ПД/ПИДрегулятор с системой ограничения дифференцирования [1], в котором сигнал, приводящий в действие схему

Известны ПИД-регуляторы, содержащие параллель-
но соединенные интегратор и дифференциатор, а также
усилитель, выходы которых подключены к входам
сумматора и соединены с нелинейным ограничителем
и входом релейного элемента [2]. Структурная схема
регулятора изображена на рис. 1. Однако в регуляторах
такого типа содержатся дополнительные сумматоры
и нелинейный блок, с помощью которых при выходе
сигнала регулятора за установленные пределы прекра-	Рис. 1. Структурная схема ПИД-регулятора

____________________________________________________________________________________________________________________________

IX Международная (XX Всероссийская) конференция по автоматизированному электроприводу АЭП-2016

- 229 -

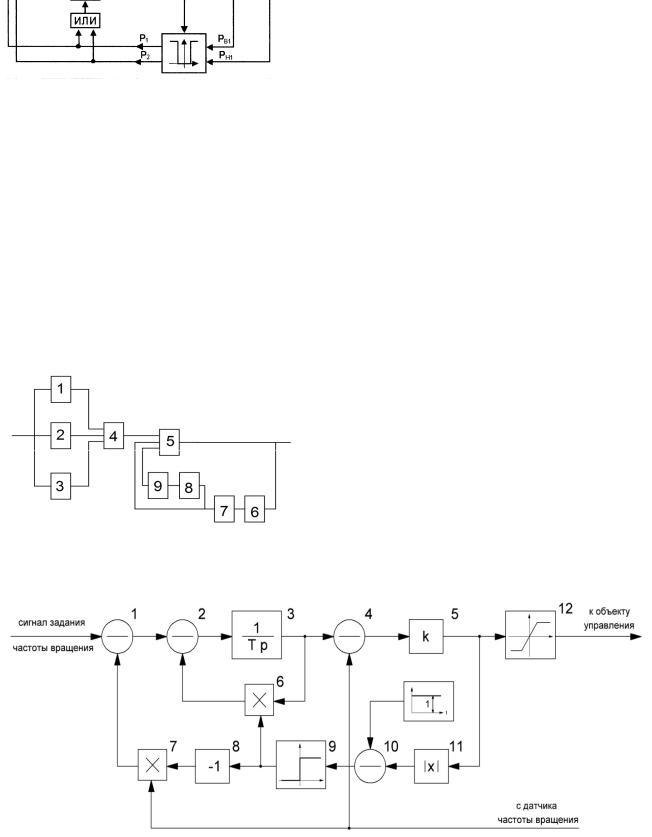
Рис. 2. Структурная схема ПИД-регулятора с системой ограничения дифференцирования

Рис. 3. Структурная схема ПИД-регулятора с блоком задержки

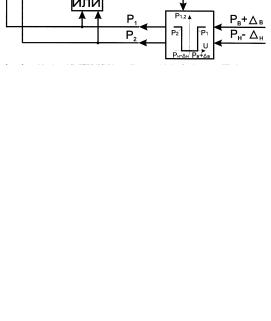
ограничения интегрирования, выдается лишь тогда, когда сигнал дифференцирования близок к нулю, структурная схема регулятора изображена на рис. 2. Однако такие регуляторы обладают сложной конструкцией и не обеспечивают установку необходимого соотношения между изменениями выходных сигналов интегратора и дифференциатора в процессе ограничения выходного сигнала всего регулятора, что снижает точность процесса регулирования.

Существует ПИД-регулятор (рис. 3), содержащий первый сумматор 4, к первому, второму и третьему входам которого соответственно через первый блок пропорционального преобразования 1, блок интегрирования 2, блок дифференцирования 3 подключен вход пропорционально-интегрально-дифференциального регулятора, выход первого сумматора соединен с первым входом второго сумматора 5 непосредственно, выход второго сумматора соединен через последовательно подключенные первый инвертор 6 и второй блок интегрирования 7, ко второму входу сумматора, выход второго блока интегрирования соединен через последовательно подключенные второй инвертор 8 и блок задержки 9 с третьим входом второго сумматора, выход второго сумматора является выходом пропорциональ- но-интегрально-дифференциального регулятора [3]. При использовании такой структуры построения регулятора, за счет введения в него блоков задержки быстродействие регулятора и системы управления в целом уменьшается.

Для увеличения быстродействия системы при заданных динамических характеристиках, а также для исключения статической и динамической ошибок регулирования предлагается использовать адаптивный регулятор частоты вращения, структурная схема которого изображена на рис. 4.

Входным сигналом быстродействующего адаптивного регулятора скорости является сигнал задания час-

.

Рис. 4. Структурная схема адаптивного регулятора частоты вращения электродвигателя: 1, 2, 4, 10 – блоки сравнения; 3 – интегратор; 5 – пропорциональное звено; 6, 7 – блок умножения; 8 – блок инвертирования сигнала; 9 – блок единичной функции входного сигнала; 11 – блок выделения модуля входного сигнала; 12 – нелинейный ограничитель тока

____________________________________________________________________________________________________________________________

IX Международная (XX Всероссийская) конференция по автоматизированному электроприводу АЭП-2016

- 230 -