6. Теорема умножения вероятностей.

Событие A называется независимым от события B, если вероятность события A не зависит от того, произошло событие B или нет. Событие A называется зависимым от события B, если вероятность события A меняется в зависимости от того, произошло событие B или нет.

Вероятность события A, вычисленная при условии, что событие B уже произошло, называется условной вероятностью события A и обозначается .

Условие независимости события A от события B можно записать в виде .

Теорема умножения вероятностей. Вероятность произведения двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную при условии, что первое имело место:

или .

Если событие A не зависит от события B, то событие B не зависит от события A. При этом вероятность произведения событий равна произведению их вероятностей:

.

Пример 14. Имеется 3 ящика, содержащих по 10 деталей. В первом ящике 8, во втором - 7 и в третьем 9 стандартных деталей. Из каждого ящика наудачу вынимают по одной детали. Найти вероятность того, что все три вынутые детали окажутся стандартными.

Вероятность того, что из первого ящика вынута стандартная деталь (событие A) равна . Вероятность того, что из второго ящика вынута стандартная деталь (событиеB) равна . Вероятность того, что из третьего ящика вынута стандартная деталь (событиеC) равна .

Так как события A, B и C независимые в совокупности, то по теореме умножения искомая вероятность равна

.

Приведем пример совместного использования теорем сложения и умножения.

Пример 15. Вероятности появления независимых событий A₁ и A₂ равны соответственно p₁ и p₂. Найти вероятность появления только одного из этих событий (событие A). Найти вероятность появления хотя бы одного из этих событий (событие B).

Обозначим вероятности противоположных событий ичерезq₁=1-p₁ и q₂=1-p₂ соответственно.

Событие A произойдет, если произойдет событие A₁ и не произойдет событие A₂, или если произойдет событие A₂ и не произойдет событие A₁. Следовательно,

.

Событие B произойдет, если произойдет событие A, или произойдут события A₁ и A₂ одновременно. Следовательно,

.

Вероятность события B можно определить иначе. Событие , противоположное событиюB состоит в том, что оба события A₁ и A₂ не произойдут. Поэтому по теореме умножения вероятностей для независимых событий получим

.

Отсюда

,

что совпадает с выражением, полученным ранее, так как имеет место тождество

.

7. Формула полной вероятности. Формула Байеса.

Теорема 1. Предположим, что события образуют полную группу попарно несовместных событий (такие события называются гипотезами). ПустьA - произвольное событие. Тогда вероятность события A может быть вычислена по формуле

. (1)

Доказательство. Так как гипотезы образуют полную группу, то , и, следовательно,.

В силу того, что гипотезы являются попарно несовместными событиями, то события также попарно несовместны. По теореме сложения вероятностей

.

Применяя теперь теорему умножения вероятностей, получим

.

Формула (1) называется формулой полной вероятности. В сокращенном виде ее можно записать следующим образом

.

Формула полезна, если условные вероятности события A вычисляются легче, чем безусловная вероятность.

Пример 16. Имеется 3 колоды по 36 карт и 2 колоды по 52 карты. Наудачу выбираем одну колоду и из нее наудачу одну карту. Найти вероятность того, что вынутая карта - туз.

Пусть A - событие, состоящее в том, что вынутая карта - туз. Введем в рассмотрение две гипотезы:

- карта вынута из колоды в 36 карт,

- карта вынута из колоды в 52 карты.

Для вычисления вероятности события A воспользуемся формулой полной вероятности:

.

Теорема 2. Предположим, что события образуют полную группу попарно несовместных событий. ПустьA - произвольное событие. Условная вероятность гипотезы в предположении, что произошло событиеA, может быть вычислена по формуле Байеса:

. (2)

Доказательство. Из теоремы умножения вероятностей для зависимых событий следует, что .

Отсюда

.

Применяя формулу полной вероятности, получим (2).

Вероятности гипотез называются априорными, а вероятности гипотез при условии, что событие A имело место, называются апостериорными. Сами формулы Байеса называются еще формулами вероятностей гипотез.

Пример 17. Имеются 2 урны. Первая урна содержит 2 белых и 4 черных шара, а вторая урна содержит 7 белых и 5 черных шаров. Наудачу выбираем урну и из нее наудачу извлекаем один шар. Он оказался черным (событие A произошло). Найти вероятность того, что шар был извлечен из первой урны (гипотеза ). Найти вероятность того, что шар был извлечен из второй урны (гипотеза).

Применим формулы Байеса:

,

.

Пример 18. На заводе болты выпускаются тремя машинами, которые выпускают соответственно 25%, 35% и 40% всех болтов. Брак продукции этих машин составляет соответственно 5%, 4%, 2%. Из продукции всех трех машин был выбран один болт. Он оказался дефектным (событие A). Найти вероятность того, что болт был выпущен первой, второй, третьей машиной.

Пусть - событие, состоящее в том, что болт был выпущен первой машиной,- второй машиной,- третьей машиной. Эти события попарно несовместны и образуют полную группу. Воспользуемся формулами Байеса

.

В результате получим

,

,

.
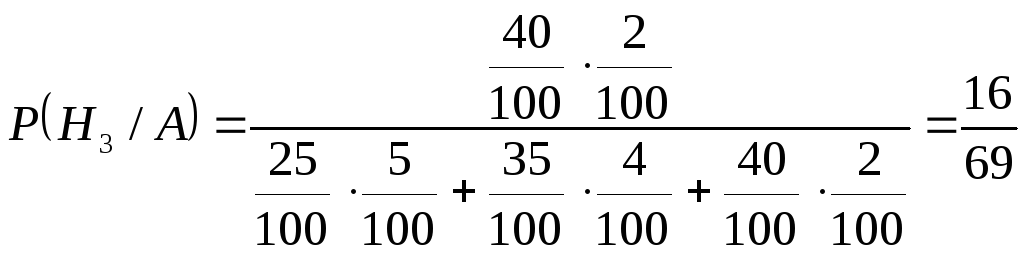