17. Нормальное распределение.

Нормальный закон распределения случайной величины X характеризуется плотностью

,

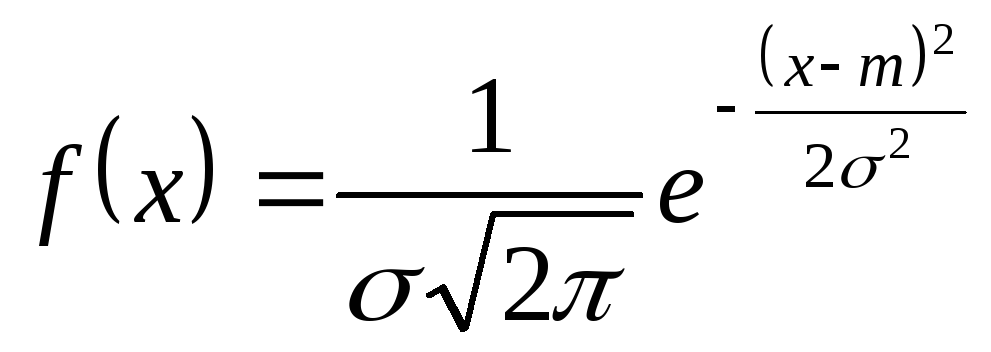где m и >0 - постоянные параметры. График этой функции называется кривой Гаусса и имеет вид, представленный на рис.6.

Рис.6. Кривая плотности нормального распределения (кривая Гаусса)

Параметр m служит абсциссой точки максимума кривой,.

Рассмотрим влияние параметра  на форму кривой. Параметр  показывает насколько пологой является кривая Гаусса. Если  велико, то кривая сильно прижата к оси абсцисс, а если  - мало, то кривая имеет ярко выраженный максимум, а все значения случайной величины группируются достаточно близко к точкеm (см.рис.).

Для нормального распределения ,,.

Нормальный закон распределения - один из самых популярных в теории вероятностей, поскольку он часто используется для описания многих случайных явлений.

Например, для случайного отклонения фактического размера изделия от стандартного, рассеяния снарядов при артиллерийской стрельбе, ошибок, связанных с измерениями и измерительными приборами, роста людей.

Нормальное распределение применяется в ситуациях, когда на изучаемое явление воздействует большое количество случайных факторов, среди которых нет сильно выделяющихся.

Если m=0, =1, то соответствующая функция распределения

называется функцией Лапласа. Эта функция табулирована и содержится во всех справочниках по теории вероятностей.

Пользуясь таблицами , легко вычислить значения функции распределенияс параметрамиm и . Действительно, так как

,

то, делая замену переменных , получим

.

Отсюда следует простая формула для вычисления вероятности попадания случайной величины X в промежуток

.

Вычислим вероятность попадания нормально распределенной случайной величины в промежуток [m-3, m+3], пользуясь таблицами :

.

Соответствующая площадь показана штриховкой на рис.4. Полученный результат можно записать следующим образом

, или .

Таким образом, вероятность того, что абсолютная величина отклонения X от m превысит утроенное значение , очень мала и равна 0,003. Такое событие является практически невозможным. Полученное свойство называется правилом "трех сигм".

Пример 1. Вес коробок с шоколадными конфетами имеет нормальное распределение со средним m=1 кг. и средним квадратическим отклонением =0,02 кг. Определить, вероятность того, что вес коробки будет в пределах от 0,98 до 1,05 кг.

Пусть X - вес коробки, тогда

.

Пример 2. Средний рост 1000 солдат равен 1,81 м со стандартным отклонением 5 см. Предположив, что рост подчиняется нормальному распределению, оценить число солдат в группе, рост которых 1) больше или равен 1,87 м, 2) лежит между 1,72 м и 1,80 м.

Пусть X - рост солдата, тогда

1)

Число солдат с таким ростом равно 0,115.1000=115.

2)

Число солдат с таким ростом равно 0,385.1000=385.

Широкое распространение нормального распределения объясняется центральной предельной теоремой: если случайная величина X представляет собой сумму очень большого числа взаимно независимых случайных величин, влияние каждой из которых на всю сумму ничтожно мало, то X имеет распределение, близкое к нормальному.

Таким образом, каково бы ни было "индивидуальное" распределение случайных величин X_i, i=1,2,…,n, с ростом n исчезает влияние этой "индивидуальности" на "поведение" случайной величины X=X₁+X₂+…+X_n.

Распределение X достаточно точно задается функцией Лапласа.