3. Вариационный анализ

А) Ряды распределения и методы их графического изображения.

а) Ряды распределения.

В экономической практике возникает потребность преобразования результатов сводки и группировки в виде статистических рядов и таблиц.

Статистические ряды распределения – упорядоченное расположение единиц (по рангу) ГС на группы, характеризующие структуру изучаемого явления и позволяющее анализировать закономерность развития границы изменений, вариации признаков и т.д.

С помощью рядов распределения решаются важнейшие задачи статистики, измерения показателей для варьирующих признаков.

1. Ряды распределения, образованные по качественному признаку (возраст, стаж, производительность) называются атрибутивными.

2. По количественному признаку – вариационные ряды.

а) по способу построения бывают:

– дискретными (прерывными), например, число студентов в группе.

– интервальными (непрерывными), базирующиеся на непрерывных изменяющихся значениях признака. Например, товарооборот, выработка.

В практике построения интервальных рядов распределения возникает вопрос о числе групп, величине интервала, о его границе.

Пример дискретного ряда распределения:

Число групп ЭГ	на 1.09.2001		на 1.12.2001
	число человек	в % к итогу	число человек	в % к итогу
1	2	3	4	5
1	15	19,48	14	17,073
2	20	25,974	22	26,829
3	25	32,467	26	31,7
4	17	22,074	20	24,39
итого	77	100%	82	100%

Интервальный ряд распределения

Пример роста детей	Число детей f	В%к итогу	куммулята
1	2	3	4
90-100	5	12,5	5
100-110	10	25	15
110-120	20	50	35
120-130	5	12,5	40
Итого	40	100%

Существуют интервальные ряды распределения с неравными промежутками. Важнейшим требованием к статистическим рядам распределения является обеспечение сравнения во времени и в пространстве. Вариационные ряды распределения с равными промежутками обеспечивают это условие, а ряды распределения с неравными промежутками используют для сравнения плотности распределения. Она определяет количество изучаемых величин в каждой группе, приходящихся на единицу величины интервала.

Б) Гистограмма, полигон, кривые распределения.

Для наглядности строят различные графики статистического распределения и, в частности, полигон и гистограмму.

В случае непрерывного признака целесообразно строить гистограмму, для чего интервал, в котором заключены все наблюдаемые значения признака, разбивают на несколько частичных интервалов и находят для каждого частичного интервала сумму частот вариант, попавших в интервал.

Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы, а высоты равны отношению суммы частот вариант к длине интервала Для построения гистограммы частот на оси абсцисс откладывают частичные интервалы, а над ними проводят отрезки, параллельные оси абсцисс на расстоянии, равном плотности частот. Площадь гистограммы частот равна сумме всех частот, т.е. объему выработки.

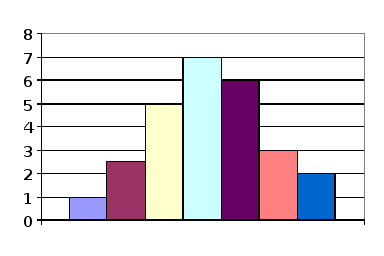
Полигоном частот называют ломаную, отрезки которой соединяют точки (x₁, n₁), (х₂, n₂), и … ,(х_k, n_k). Для построения полигона частот на оси абсцисс откладывают варианты х_i, а на оси ординат - соответствующие им частоты n_i,

Точки (х_i, n_i,) соединяют отрезками прямых и получают полигон частот.

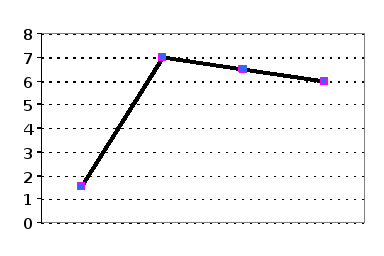
В) Другие методы графического изображения.

Результаты обработки информации выражаются не только в табличной форме, но и в форме графиков и диаграмм, то есть облегчается интерпретация информации ряда распределения.

График - наглядное изображение статистических величин и их соотношений с помощью точек, геометрических фигур и линий в координатной системе.

Диаграмма - графическое изображение, наглядно показывающее соотношение между сравниваемыми величинами.

Линейные графики: гистограммы, полигоны, кумулята, связаны с графическим отображением непрерывных данных, сгруппированных в виде ряда распределения таким образом, что по оси У откладываются частоты рядов распределения, а по оси Х- переменные значения (признаки рядов распределения).

Во всех случаях, когда статистические данные поддаются группировке, можно пользоваться диаграммой для упорядочения предварительно собранной информации.

Виды диаграмм:

1) столбиковые;

2) полосовые:

а) с группировкой,

б) составные,

в) простые;

3) линейные;

4) пиктограмма;

5) стратиграмма;

6) круговые:

а) процентные,

б) единичные.

Столбиковые диаграммы строятся следующим образом: по оси X откладываются года, а по оси У - результаты измерения: %, тонны, штуки и т.п. Столбики располагаются вертикально, они не соприкасаются и имеют любую, но одинаковую ширину.

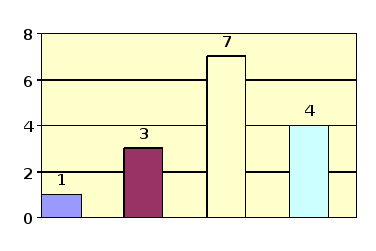
Полосовые:

А) простая - по оси X откладываются значения признака, а по оси У- года.

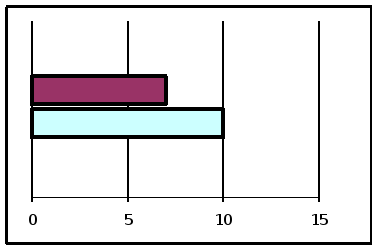
Б) Составные - для представления связанных групп данных на одном графике применяется метод сравнения в кумулятивной форме. Например, выпуск продукции A, В, С. Большое внимание уделяется суммированию групп, часто их представляют разными цветами.

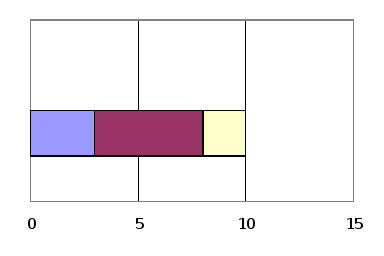
В) с группировкой - используется в том случае, если хотят сравнить группы данных. По оси X располагают значения признака, а по оси У - года.

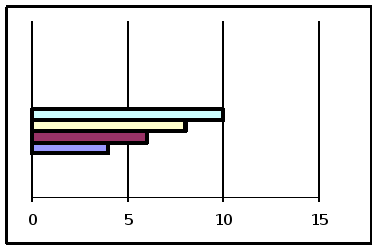
Линейная диаграмма представляет соотношение между временем (по оси X) и частотами по оси У. Соединение точек анаализа даёт кривую, которая соответствует верхней линии стратиграммы.

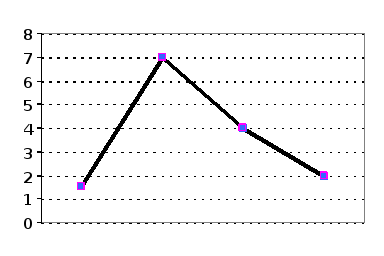
Пиктограмма - рисованная диаграмма. Она чаще используется в финансовых отчётах и для информирования широкой публики. В ней используется условное изображение.

Стратиграмма - это графическая диаграмма, которая показывает изменение двух или более категорий чисел.

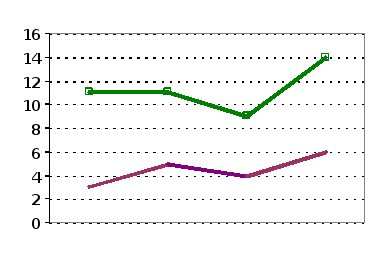
Круговая диаграмма бывает двух типов:

А) процентная - когда, анализируя один год,

за 100% берут круг делят его на части

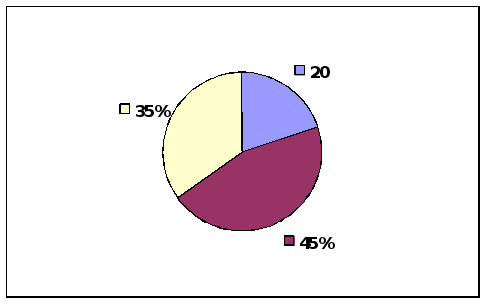
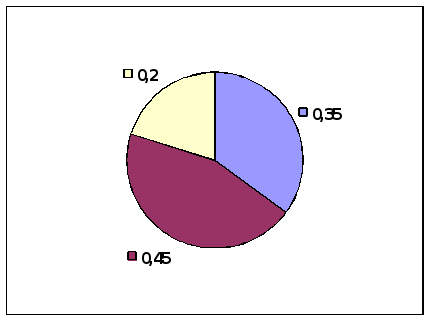
Б) единичная

Все диаграммы, кроме круговых, могут использоваться при изменении данных во времени. Одиночная круговая диаграмма таких изменений не даёт. Только с помощью нескольких круговых диаграмм можно показать изменение признака во времени

Б) Характеристики центра распределения.

а) Средняя арифметическая.

Пусть изучается генеральная совокупность относительно количественного признака X, и из неё извлечена выборка объемом n..

Выборочной средней арифметической называют среднее арифметическое значение признака выборочной совокупности. Она вычисляется по следующей формуле:

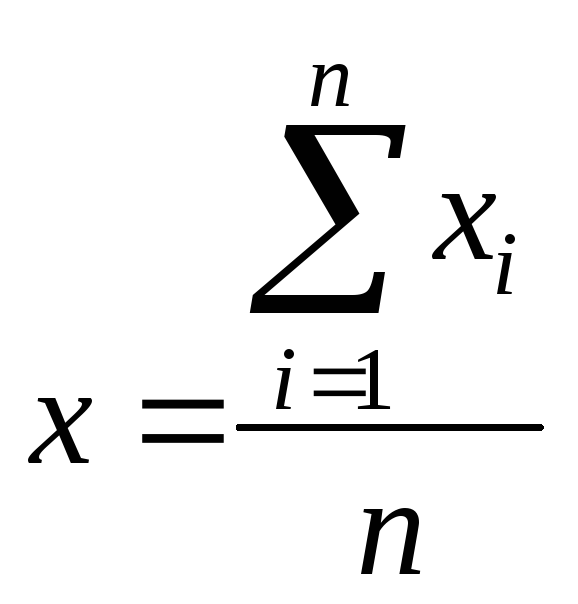, где n – число элементов выборки.

Для средней арифметической генеральной совокупности формула вычисления следующая:

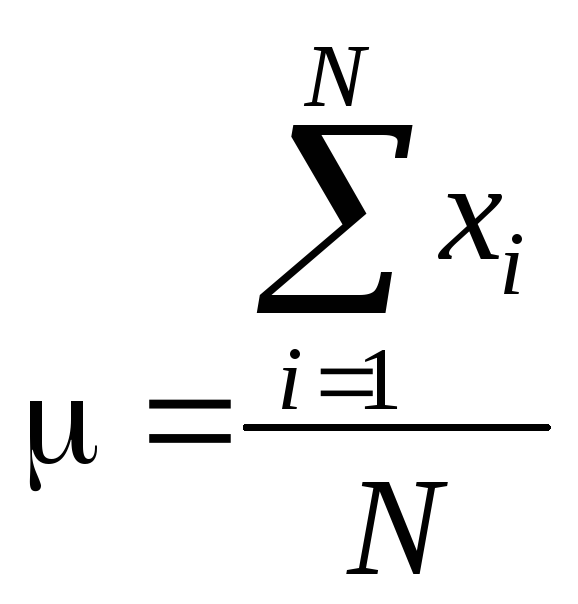, где N – число элементов генеральной совокупности.

При простой средней арифметической частота каждого варианта f = 1.

Средняя арифметическая сгруппированных данных.

В таблице приведены данные о размере заработной платы некоторого числа рабочих.

xi	f	xif
1	2	3
12	10	120
7	35	245
15	5	75
	Σ50	Σ440

Формула вычисления:

Чтобы найти среднюю арифметическую для дискретного ряда распределения, нужно:

1) Построить граф 3 (x_if) и найти произведения варианты на частоту в каждой строке;

2) Подсчитать сумму произведения Σx_if;

3) Определить общее число случаев Σf;

4) Найти частное отношение суммы произведений вариантов на частоты к сумме частот.

Полученная величина и будет искомой средней арифметической дискретного ряда распределения сгруппированных данных.

Средняя арифметическая интервального ряда распределения рассчитывается в тех случаях, когда в столбце вариантов не одно, а два значения, показывающие верхнюю и нижнюю границу. Среднее значение интервала находится путём отыскания простой х_сер. Между верхней и нижней границами интервала. Число случаев f умножается на эту величину, и находится сумма этих произведений. Формула вычисления в этом случае:

Свойства средней арифметической:

1) Сумма отклонений отдельных вариантов от средней арифметической равна нулю.

2) При умножении или делении всех частот распределения средняя арифметическая остаётся неизменной.

3) Среднее отклонение , как и полуразмах кварцидей, децилей, редко применяется в хозяйственных расчётах для сравнения степени вариации рядов распределения. При вычислении среднего отклонения суммируются абсолютные значения этих отклонений. А при вычислении среднеквадратического отклонения суммируются квадраты этих отклонений.

б) Структурные средние.

Для характеристики структуры генеральной совокупности используются показатели особого рода, которые называются структурными средними: Мо и Ме.

Мода Мо – это наиболее часто встречающийся признак в вариационном ряду распределения, то есть варианта, которая имеет наибольшую частоту.

Или в другой форме:

где x₀ – нижняя граница модального ряда распределения,

h – шаг распределения,

f_{мод 2} – частота модального ряда распределения,

f_{мод 1} – предшествующая частота,

f_{мод 3} – частота, следующая за частотой модального ряда распределения.

Медиана Ме – это середина упорядоченного ряда распределения, то есть варианта, которая делит, вариационный ряд на две части, равные по числу вариант.

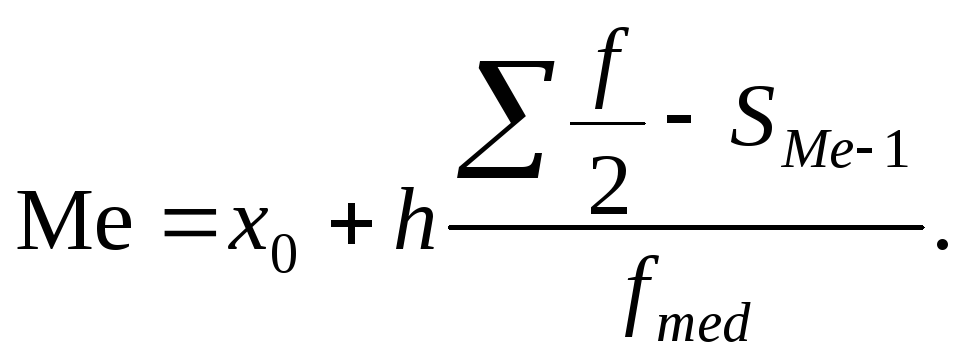
в) Квартили, децили, процентили.

Хотя они и не характеризуют центр рядов рарпределения, они, подобно медиане (она делит ряд распределения пополам), делят ряд распределения:

Квартили – на 4 части,

Децили – на 10 частей,

Процентили – на 100 частей.

г) Другие евды средних. Методы их расчета.

Взвешенная средняя арифметическая.

До сих пор при определении средней арифметической были те признаки, средние значения которых мы находили. Частоты f показали, сколько раз встречается тот или иной признак. Но не всегда можно найти среднюю арифметическую, базируясь на один признак элементов статистической совокупности, в ряде случаев надо привлекать еще один признак. Например, при продаже хлеба, кроме цены, выписанной из прейскуранта цен, который является не результатом наблюдений, появляется количественный признак -различное распределение веса того или иного сорта. Формула средней арифметической ряда распределения отличается от формулы средней арифметической взвешенной тем, что вместо частот f появляются веса w.

Алгоритм нахождения взвешенной средней арифметической:

1) Устанавливаются правильные веса,

2) Находится произведение x_iw

3) Подсчитывается сумма ,

4) Определяется сумма ,

5) Находится взвешенная средняя арифметическая.

Взвешенная средняя арифметическая аналогична центру тяжести в механике, т.е. той точке, в которой происходит равновесие сил. Для итогов взвешивания важны не абсолютные величины, а их соотношения.

Средняя гармоническая вычисляется, когда мы имеем дело с обратными величинами, то есть когда возникает необходимость вычислить среднюю из величин, обратно пропорциональных изучаемому явлению. Например:

1) Отношение производительности к трудоёмкости даёт нам среднюю трудоёмкость.

2) Отношение износа фондов к сроку службы фондов показывает среднее значение срока службы фондов.

3) Отношение уровня рождаемости к общему числу людей даёт среднее число людей, приходящихся на одного рождаемого.

Формула средней гармонической:

1) Простая: 2) Взвешенная:

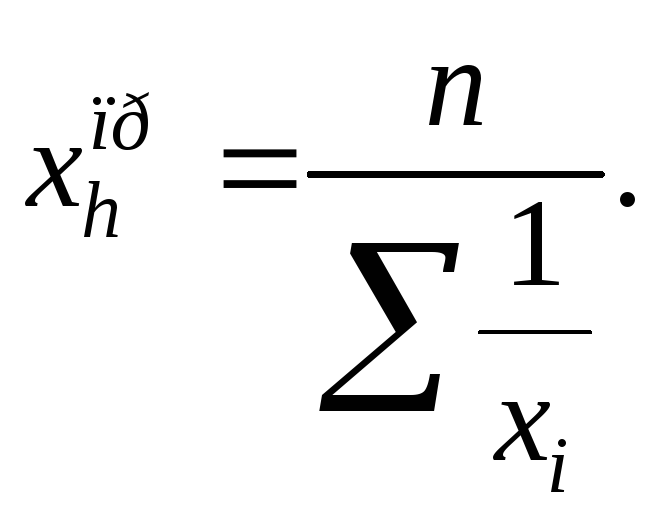
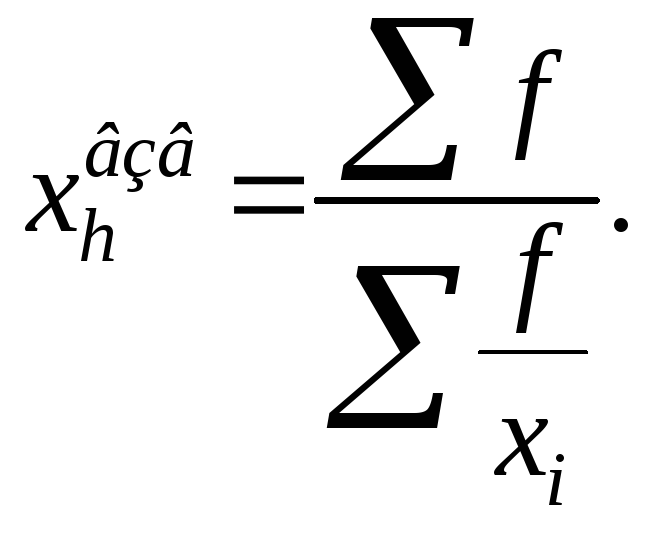
где f – частота,

х_i – изучаемый признак.

Средняя геометрическая – применяется при вычислении средних темпов роста.

1) Простая:

где –произведения признаков.

2) Взвешенная:

х_g всегда меньше .

Расстояние между модой и средней арифметической показывает размер пути, который надо пройти основной массе коллектива. Это и будет прогрессивное усвоение опыта передовиков производства, то есть средняя прогрессивная .

Медиана графическая – это точка на оси абсцисс, в которой площадь графика делится на две равные части.

Мода графическая – это абсцисса точки максимума кривой распределения. Для дискретных рядов – это значение признака, который чаще всего встречается. Для интервальных рядов – это значение признака, который характеризует максимальную плотность распределения.

В) Характеристики вариации.

а) Размах вариации.

Размах вариации является простейшей характеристикой рассеяния вариационного ряда. Размахом вариации R называют разность между наибольшей и наименьшей вариантами:

б) Стандарт отклонений.

Выборочным средним квадратическим отклонением (стандартом) называют квадратный корень из выборочной дисперсии.

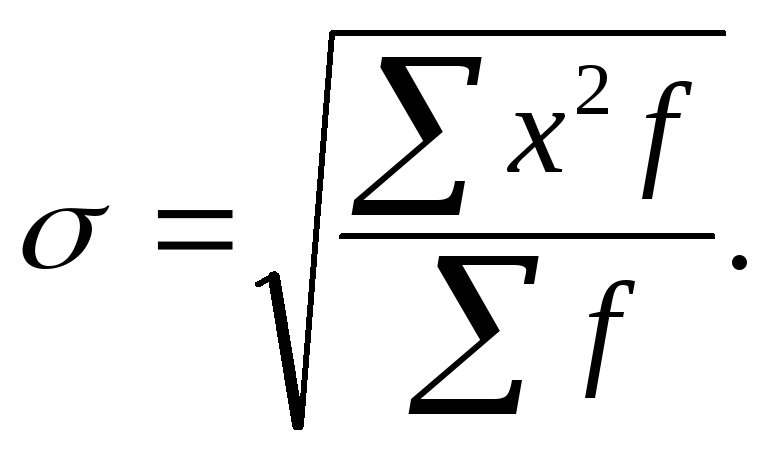
Выборочной дисперсией называют среднее арифметическое квадратов отклонения наблюдаемых значений признака от их среднего значения. То есть выборочная дисперсия есть средняя взвешенная квадратов отклонений с весами, равными соответствующим частотам.

в) Коэффициент вариации.

Коэффициент вариации служит для сравнения величин рассеяния по отношению к выборочной средней двух вариационных рядов: тот из рядов имеет большее рассеяние по отношению к выборочной средней, у которого коэффициент вариации больше. Коэффициент вариации – безразмерная величина, поэтому он пригоден для сравнения рассеяния вариационных рядов, варианты которых имеют различную размерность, например, если варианты одного ряда выражены в сантиметрах, а другого – в граммах.

Коэффициентом вариации V называют выраженное в процентах отношение выборочного среднего квадратического отклонения к выборочной средней.

г) Измерение асимметрии, эксцесса.

Асимметрией теоретического распределения называют отношение центрального момента третьего порядка к кубу среднего квадратического отклонения:

Асимметрия положительна, если «хвост» кривой распределения находится: справа; асимметрия отрицательна, если «хвост» кривой распределения располагается слева.

Практически определяют знак асимметрии по расположению кривой распределения относительно моды (точки максимума): если «длинная часть» кривой расположена правее моды, то асимметрия положительна, если слева – отрицательна.

Для оценки крутости, то есть большего или меньшего подъема кривой теоретического распределения по сравнению с нормальной кривой, пользуются характеристикой – эксцессом.

Эксцессом теоретического распределения называют характеристику, которая определяется равенством:

Для нормального распределения эксцесс равен нулю. Поэтому если эксцесс некоторого распределения отличен от нуля, то кривая этого распределения отличается от нормальной кривой: если эксцесс положительный, то кривая имеет более высокую и острую вершину, чем нормальная кривая. Если эксцесс отрицательный, то сравниваемая кривая имеет более низкую и плоскую вершину, чем нормальная кривая.

д). Расчёт моментов.

Статистика – это наука о распределении. Показатели вариации: мода, медиана, среднеквадратическое отклонение не дают достаточной информации о законе распределения. Для полноты анализа вводятся моменты распределения. Это понятие пришло из механики. Момент определяет эффективность действия силы на придание телу вращательного движения. Статистический момент характеризует силу, приложенную к варианте. Моменты – это обобщающие характеристики, определяющие характер распределения:

Моментом к-^го порядка называют изменения к-^тых степеней отклонения признака х от некоторой постоянной А. В зависимости от этой постоянной различают следующие моменты:

1) Начальные,

2) Начальные относительно х_о (условные),

3) Центральные.

1) Начальный момент при А=0

1а) Начальный момент нулевого порядка при к=0

1б) Начальный момент первого порядка при к=1

1в) Начальный момент второго порядка при к=2

1г) Момент третьего порядка при к=3

1д) Момент четвёртого порядка при к=4

2) Начальный момент относительно х_о

при А=х_о, где х_о – произвольно выбранная величина из ряда распределения.

3) Центральный момент при А=х