практикум по ягф (готовое)

Математическим ожиданием дискретной случайной величины назы-

n

вается число М = xi pi . Если мы будем наблюдать случайную величину

1

много раз, то среднее арифметическое из этих значений будет близко к М Дисперсией дискретной случайной величины называется число

D = M ( -M )2

Дисперсия характеризует разброс случайной величины вокруг средне-

го значения.

Случайная величина называется непрерывной, если она может при-

нимать значения из некоторого интервала (a, b). Непрерывная случайная ве-

личина задается с помощью функции р(х)>0, которая называется плотностью

вероятности случайной величины .

Математическим ожиданием непрерывной случайной величины

	b
называется число М	= xp(x)dx
	a
Дисперсией	непрерывной случайной величины называется число
	b
	D = (x M )2 p(x)dx
	a

При решении задач ММК приходится моделировать случайные величи-

ны с различными законами распределения. В теории метода доказывается,

что для того, чтобы вычислять значения таких величин, достаточно уметь на-

ходить значения какой-либо одной (стандартной) величины, так как всегда можно подобрать такую функцию от этой величины, которая имеет требуе-

мый закон распределения. В качестве стандартной выбирают случайную ве-

личину равномерно распределенную в интервале (0, 1).

Cлучайная величина называется равномерно распределенной в интер-

вале (0, 1), если еѐ плотность распределения имеет вид:

41

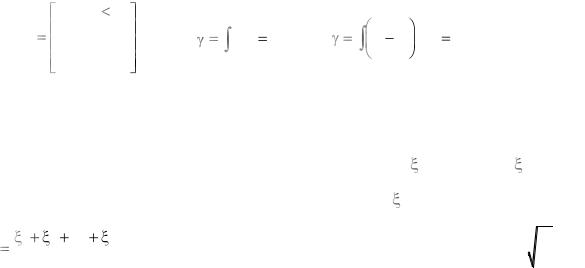
	0	x 0		1				1			2
					1					1			1
	p(x) 1	0<x<1 ;	М	xdx		;	D	x			dx			;
					2				2			12
	0	x>1		0				0
	Основная	идея, заложенная в ММК – сведение							задачи к расчету мате-

матических ожиданий. Например, чтобы приближѐнно вычислить некоторую

величину Х надо придумать такую случайную величину				, чтобы М	=Х
	Тогда, вычислив N известных значений величины			, можно считать,
		1 2 .... n
что	X		. Ошибка вычислений пропорциональна величине			B	,
						N
		N

где В некоторая - константа. Отсюда следует, что для того чтобы уменьшить ошибку вычислений, например в 10, раз необходимо увеличить число испы-

таний (объѐм вычислений) в 100 раз. Отметим, что одну и ту же задачу мож-

но решать различными вариантами ММК, которым отвечают различные зна-

чения В. Во многих случаях удается значительно увеличить точность, выбрав способ расчета, которому соответствует меньшее значение В.

2.2. Получение случайных чисел на ЭВМ

Различают три способа получения на ЭВМ случайных чисел: таблицы случайных чисел, генераторы случайных чисел и метод псевдослучайных чи-

сел.

Таблицы случайных чисел. Предположим, что мы осуществили N независи-

мых опытов, в результате которых получили N cслучайных чисел (цифр). Та-

кие числа можно получить, например, с помощью электронной рулетки. За-

писав эти цифры в порядке возрастания, и объединив их в группы, получим таблицу случайных цифр. Ниже приведена строка таблицы случайных цифр объединѐнных в группы по две.

84

75

45

67

04

38

13

26

42

98

42

Подобную таблицу можно ввести в память ЭВМ. Если в ходе расчета нам понадобится значение случайной величины равномерно распределенной в интервале (0, 1), мы будем брать указанные пары цифр, умноженные на 0,01.

Чтобы случайные числа, полученные с помощью такой таблицы, не повто-

рялись, она должна содержать большое количество цифр (более миллиона)

Обращение к таким таблицам сильно замедляет счет, поэтому применение таблиц случайных цифр в ММК ограничено.

Генераторы случайных чисел. Генераторами (датчиками) случайных чи-

сел называют различные технические устройства, вырабатывающие случай-

ные величины. Чаще всего для построения датчиков используют «шумящие» радиоэлектронные приборы (диоды, газотроны и др.) Примером датчика, вы-

рабатывающего случайные двоичные цифры может быть следующий: если за некоторый фиксированный промежуток времени t уровень шума прибора превысил данный порог четное число раз, то записывается 0, а если нечет-

ное число раз, то записывается 1. Если вероятности появления 0 и 1 в таком процессе равны, то можно считать, что устройство вырабатывает случайную последовательность двоичных цифр.

К достоинствам применения генераторов случайных чисел относятся быстрота их получения, практически неограниченный запас чисел и отсутст-

вие необходимости занятия большого объѐма оперативной памяти ЭВМ.

Однако, этот метод не свободен от недостатков. Во-первых, приходится со-

держать и эксплуатировать дополнительные устройства, вырабатывающие случайные числа. Вовторых, числа вырабатываемые датчиком нельзя вос-

произвести, что затрудняет контроль расчетов.

Псевдослучайные числа. Пригодность случайных чисел определяется, в

конечном счете, не процессом их получения, а тем удовлетворяют они неко-

торым тестам. В этом случае они могут быть сосчитаны по какой-либо фор-

муле и проверены на «случайность» с помощью специальных тестов. Числа,

получаемые по заданной формуле и имитирующие значение случайной вели-

43

чины равномерно распределенной в интеравале (0, 1) называются псевдо-

случайными.

К достоинствам метода псевдослучайных чисел относится простота и высокая скорость их получения, а также возможность их воспроизведения.

Подавляющее большинство расчетов ММК в настоящее время осуществляет-

ся с помощью псевдослучайных чисел.

2.3. Разыгрывание дискретных случайных величин

Допустим нам нужно получить значение дискретной случайной величи-

ны с распределением		x1 x2..... xn	,	где х1 , х2 …. хn возможные значения
		p1 p2..... pn
случайной величины,	P1, P2, …..Pn соответствующие им вероятности.
Рассмотрим интервал (0, 1) и разобьѐм его на n интервалов, длины кото-
рых будут равны P1,	P2, …..Pn. Координатами точек деления будут значения:
P1, P1 +P2, P1 +P2, +…. Pn-1.
Каждый раз, когда нам нужно будет разыграть значения					будем выби-
рать очередное значение случайной величины равномерно распределѐнной
в интераале (0, 1). Затем сравниваем				с величиной P1. Если	< P1, то =

х1, если > P1, то сравниваем	с P1 +P2. Если P1 < < P1 +P2 , то					= х2 .
Если > P1 +P2, то сравниваем	с P1 +P2 +P3 и.т.д.
Пример: Разыграть 10 значений случайной величины (возможная						оценка
успевающего студента на экзамене).
	3		4	5
	0.1		0.8	0.1

В качестве значений выберем пары чисел из строки таблицы случайных цифр, умноженных на 0.01. Тогда =0.84; 0.75; 0.45; 0.76; 0.04; 0.38; 0.13; 0.26; 0.42; 0.94.

44

Согласно нашей схеме значениям <0.1 отвечают оценка «3», значениям

0.1 < < 0.9 оценка «4», а значениям 0.9 < < 1 оценка «5». Следовательно,

мы получаем следующие разыгранные значения оценки студента: 4, 4, 4, 4, 3, 4, 4, 4, 4, 5.

2.4. Разыгрывание непрерывной случайной величины

Предположим, что случайная величина непрерывна в интервале (a, b)

и имеет плотность вероятности распределения р(х). Можно доказать, что значение можно находить из уравнения:

p(x)dx

a

где равномерно распределенная в интервале (0, 1) случайная величина.

Пример: Разыграть значения равномерно распределѐнной в интервале (-1, 1).

Случайная величина называется равномерно распределѐнной в интер-

вале (-1, 1),если еѐ плотность распределения имеет вид:

0 x 1 p(x) 0.5 -1<x<1

0 x>1

Чтобы разыграть значения , составляем уравнение:

dx

1 2

Вычисляя интеграл, получаем выражение для розыгрыша :

21

2.5.Моделирование похождения нейтронов через вещество

Известно, что взаимодействие нейтронов и гамма квантов с веществом носит вероятностный характер. Во многих задачах ядерной геофизики требу-

ется найти среднее число частиц, регистрируемых детектором, их энергию и

45

другие макроскопические характеристики. Решение подобных задач эффек-

тивно ММК. Ниже рассматривается простейший вариант задачи о прохожде-

нии нейтронов через бесконечный пласт.

Пусть на однородный бесконечный пласт мощностью H падает N ней-

тронов с энергией Е перпендикулярно поверхности пласта. При столкнове-

нии с ядрами нейтроны могут лишь упруго рассеиваться и поглощаться.

Предположим для простоты, что энергия нейтронов при рассеянии не меня-

ется и любое направление рассеяния равновероятно (изотропное рассеяние).

Требуется найти количество нейтронов, прошедших сквозь пласт N1, количе-

ство нейтронов, отражѐнных пластом N2 и количество нейтронов, поглощен-

ных в пласте N3.

Процесс взаимодействия нейтронов с ядрами вещества пласта характе-

ризуется суммарным микроскопическим сечение взаимодействием При этом, п р где п и р микроскопические сечения поглощения

и рассеяния соответственно.

Для характеристики суммарного эффекта взаимодействия нейтронов с веществом пласта воспользуемся понятием макроскопического сечения

взаимодействия .

Для моноэлементной среды связь между и имеет вид

n			NА	,
	я
			А
где nя число ядер в единице объѐма вещества; N A					6.02 1023	– число Авогадро,
– плотность вещества, А – атомная масса элемента.
Аналогично предыдущему:		П Р , где			П и Р	макроскопические

сечения поглощения и рассеяния. При этом вероятность поглощения нейтро-

на при столкновении с ядром равна	П	, а вероятность рассеяния	Р	.
Моделирование траекторий будем начинать с момента, когда нейтроны
оказались на поверхности пласта.	Длина свободного пробега нейтрона -

случайная величина равная пробегу нейтрона между столкновениями.

46

Из теории известно, что она может принимать любые значения с плот-

ностью вероятности р(x)				e x
Вычислим среднее значение длины свободного пробега:
					x	e x dx	1
				0
Таким образом, средняя длина свободного пробега нейтрона равна об-
ратной величине полного макроскопического сечения.
Формулу для розыгрыша длины свободного пробега									можно получить
из уравнения	e	x dx
	0
Вычисляя интеграл, получим
						1 e	,
где	ln(1	)	.
Учитывая, что величина 1						, распределена также как и , получим
окончательную формулу для розыгрыша

ln

Остается выяснить, как выбирать случайное направление нейтрона по-

сле рассеяния. Можно доказать, что требование изотропности рассеяния рав-

носильно требованию чтобы косинус угла рассеяния был равномерно рас-

пределѐн в интервале (-1, 1).

Таким образом, розыгрыш угла рассеяния следует проводить по форму-

ле: cos	2	1
Итак,		на первом этапе вычисляем случайную величину и проверяем
условие	>H. Если условие выполнено, то нейтрон прошел через пласт, счет

траекторий заканчивается и добавляется единица к счетчику прошедших час-

тиц. В противном случае, проверяется условие <0. Если выполнено это

условие, то счет траекторий заканчивается и добавляется единица к числу

47

отраженных частиц. Если и это условие не выполнено, т.е. 0< <H, значит,

произошло столкновение. Тогда с помощью нового случайного числа про-

веряем условие П . Если неравенство выполнено, то добавляется единица

к числу поглощенных частиц и переходим к новой траектории. Если нет, то считаем, что нейтрон испытал рассеяние, разыгрываем новое значение угла рассеяния по формуле: cos 2 1 и повторяем все сначала.

После того как будут рассчитаны все N траекторий, получим, что N1

нейтронов прошли через пласт, N2 нейтронов отразились, а N3 поглотились в пласте.

Отметим, что ММК позволяет решать значительно более сложные зада-

чи, например, расчет числа частиц, попавших в детектор применительно к плоской и скважинной геометрии. При этом среда может состоять из раз-

личных веществ и иметь любую геометрическую форму, энергия частиц при столкновении может изменяться, а рассеяние не быть изотропным.

48

ЛАБОРАТОРНАЯ РАБОТА № 3 РАСЧЕТ ПРОХОЖДЕНИЯ НЕЙТРОНОВ ЧЕРЕЗ ПЛАСТ БЕСНОНЕЧНОГО

ПРОСТИРАНИЯ МЕТОДОМ МОНТЕ-КАРЛО

Постановка задачи

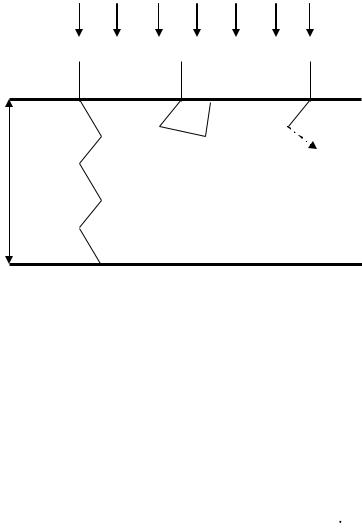
Пусть на пласт мощностью H бесконечного простирания, состоящего из смеси SiO2 и B2O3 падает N0 нейтронов перпендикулярно поверхности пласта (см. рис. 25).

N0

n01

N2

N3

H

N1

Рис.25. Прохождение нейтронов через пласт. N0 – начальное количество нейтронов; N1 –

количество нейтронов, прошедших сквозь пласт, N2 – количество отраженных нейтронов;

N3 – количество нейтронов, поглощенных в пласте

Рассчитать N1 – количество нейтронов, прошедших сквозь пласт, N2 – количество отраженных нейтронов; N3 – количество нейтронов, поглощенных в пласте. Принять, что плотность пласта 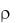составляет 3 106 кг/м3, мощность пласта H = 0,1 м, N0 = 100000 нейтронов. Концентрация B2O3 изменяется от 0,01 до 1 %, а SiO2 от 99,99 до 99 % соответственно.

49

Микроскопические сечения рассеяния и поглощения для элементов,

входящих в состав пласта, приведены в таблице 3.

			Таблица 3
	Микроскопические сечения рассеяния и поглощения
		Сечение поглощения	Сечение рассеяния
Элемент		п 1028 м2	р 1028 м2
105 B		760	4
168 O		0,0002	4,2
1428 Si		0,16	1,7

Вычислим макроскопические сечения поглощения ( п) и рассеяния ( р)

пласта для случая:

CSiO2 99%

CB2O3 1%

Макроскопические сечения					п и	р	пласта рассчитываются по формулам:
			NSiO (	Si	2	O	NB O (2		B	3	O
		П		П		П )			П		П )
			2				2	3
			NSiO (	Si	2	O	NB O (2		B	3	O
		Р		Р		Р )			Р		Р ),
			2				2	3
где NSiO	и NB O – количество атомов в единице объема SiO2 и B2O3 соответ-
2	2	3

ственно. Количество атомов в единице объема (Nx) определяется по формуле:

N			N A		CX	,
	X
				X
где – плотность вещества, N A 6.02 1023					– число Авогадро, CX – концентра-
ция вещества, X – молекулярная масса вещества.
Тогда количество атомов NSiO		и NB O			будет равно соответственно:
	2	2		3
		50