424мп
.docЗадача 6. Диаметры деталей распределены по нормальному закону. Среднее значение диаметра равно d = 15 мм, среднее квадратическое отклонение σ = 4 мм. Найти вероятность того, что диаметр наудачу взятой детали будет больше α = 15 мм и меньше β = 19 мм; вероятность того, что диаметр детали отклонится от стандартной длины не более, чем на Δ = 1.5 мм.
Решение:
Вероятность того, что Х примет значение,
принадлежащее интервалу
,
равна
,
где Ф(·) – функция Лапласа.
Вероятность того, что отклонение
случайной величины X,
распределённой по нормальному закону,
от математического ожидания а не
превысит по абсолютной величине величину
равна
,
то есть для наших данных имеем
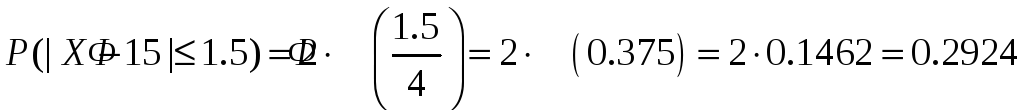или 29.24 %.
Задача 7. Признак Х представлен дискретным выборочным распределением в виде таблицы выборочных значений. Требуется:
-
составить интервальное распределение выборки;
-
построить гистограмму относительных частот;
-
перейти от составленного интервального распределения к точечному выборочному распределению, взяв за значения признака середины частичных интервалов;
-
построить полигон относительных частот;
-
найти эмпирическую функцию распределения и построить ее график;
-
вычислить все точечные статистические оценки числовых характеристик признака: среднее X; выборочную дисперсию и исправленную выборочную дисперсию; выборочное с.к.о. и исправленное выборочное с.к.о. s;
-
считая первый столбец таблицы выборкой значений признака Х, а второй – выборкой значений Y, оценить тесноту линейной корреляционной зависимости между признаками и составить выборочное уравнение прямой регрессии Y на Х.
Вариант № 5. Исходные данные.
|
54,3 |
58,1 |
45,1 |
46,1 |
62,3 |
63,4 |
88,9 |
46,1 |
60,6 |
62,4 |
|
14,1 |
25,1 |
49,1 |
25,6 |
50,1 |
48,1 |
46,6 |
59,1 |
53,1 |
52,8 |
|
79,1 |
67,1 |
19,4 |
59,1 |
50,6 |
57,1 |
66,9 |
82,6 |
71,1 |
38,6 |
|
54 |
52,9 |
53,8 |
73,1 |
34,1 |
36,1 |
26,5 |
56,1 |
74,5 |
63,1 |
|
27,9 |
54,1 |
75,3 |
27,1 |
51,9 |
51,5 |
54,9 |
82,4 |
31,1 |
60,7 |
|
55,4 |
62,7 |
32,5 |
46,5 |
58,5 |
55,8 |
52,9 |
53,5 |
61,6 |
51,7 |
|
37,6 |
54,1 |
31,1 |
43,8 |
61,6 |
51,9 |
22,5 |
39,7 |
32,5 |
41,7 |
|
53,6 |
30,8 |
58,1 |
72,7 |
33,4 |
66,8 |
35,3 |
47,9 |
48,1 |
73,2 |
|
50,4 |
80,8 |
41,2 |
73,3 |
43,4 |
34,1 |
47,1 |
50,2 |
94,1 |
67,1 |
|
34,2 |
47,9 |
68,9 |
26,1 |
42,9 |
46,4 |
68,9 |
45,1 |
21,9 |
34,1 |
Решение:
1) Составим интервальное распределение выборки.
Число групп разбиения определим из формулы Стерджесса:
групп.
Максимальное значение в выборке равно
94.1, минимальное – 14.1, размах равен 80,
тогда величина интервала
.
При попадании значения на границу
интервала будем относить его к меньшему
интервалу.
Интервальный ряд распределения имеет вид:
|
Интервал |
Частота, mi |
Относительная частота, pi |
|
14.1 – 24.1 |
4 |
0.04 |
|
24.1 – 34.1 |
15 |
0.15 |
|
34.1 – 44.1 |
11 |
0.11 |
|
44.1 – 54.1 |
31 |
0.31 |
|
54.1 – 64.1 |
20 |
0.2 |
|
64.1 – 74.1 |
11 |
0.11 |
|
74.1 – 84.1 |
6 |
0.06 |
|
84.1 – 94.1 |
2 |
0.02 |
2) Строим гистограмму относительных
частот. Ширина отдельного интервала
h=9.2. Гистограмма частот – это ступенчатая
фигура, состоящая из прямоугольников,
основания которых – частичные интервалы,
высоты равны отношению частоты к длине
частичного интервала (плотность частоты)
.
-
№ колодца
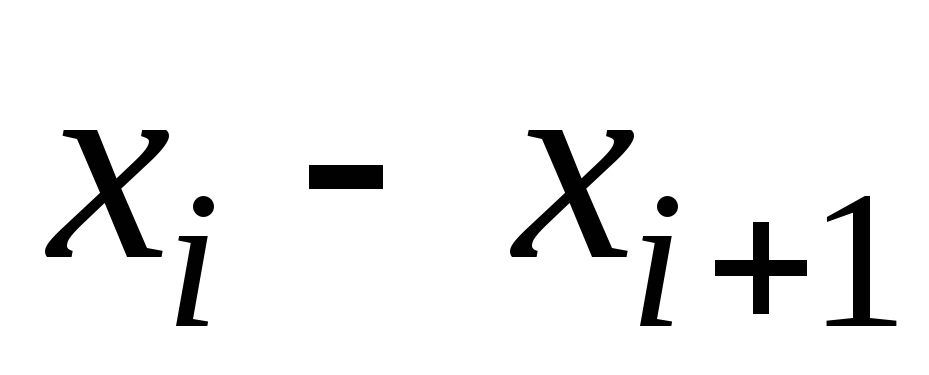
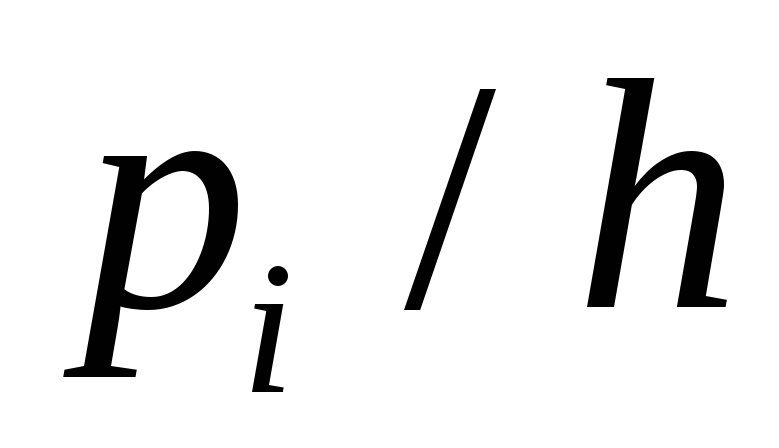
1
14.1 – 24.1
0,04
0,004
2
24.1 – 34.1
0,15
0,015
3
34.1 – 44.1
0,11
0,011
4
44.1 – 54.1
0,31
0,031
5
54.1 – 64.1
0,2
0,020
6
64.1 – 74.1
0,11
0,011
7
74.1 – 84.1
0,06
0,006
8
84.1 – 94.1
0,02
0,002
1
0,1
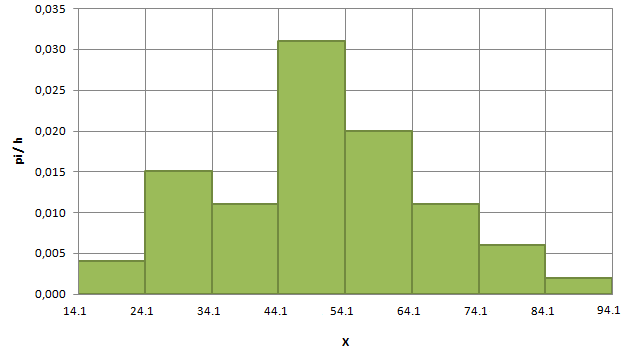
Гистограмма относительных частот
3) Перейдем от интервального ряда к дискретному, положив в качестве дискрета интервала его середину:
|
Варианта, xi |
Частота, mi |
Относительная частота, pi |
|
19,1 |
4 |
0,04 |
|
29,1 |
15 |
0,15 |
|
39,1 |
11 |
0,11 |
|
49,1 |
31 |
0,31 |
|
59,1 |
20 |
0,2 |
|
69,1 |
11 |
0,11 |
|
79,1 |
6 |
0,06 |
|
89,1 |
2 |
0,02 |
4) Построим полигон относительных частот
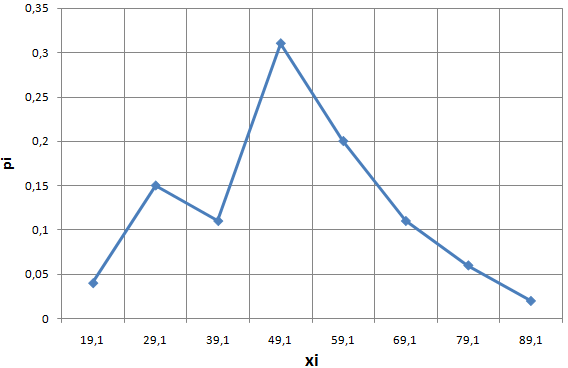
5) Запишем эмпирическую функцию распределения. Для записи функции будем накапливать соответствующие относительные частоты, тогда
.
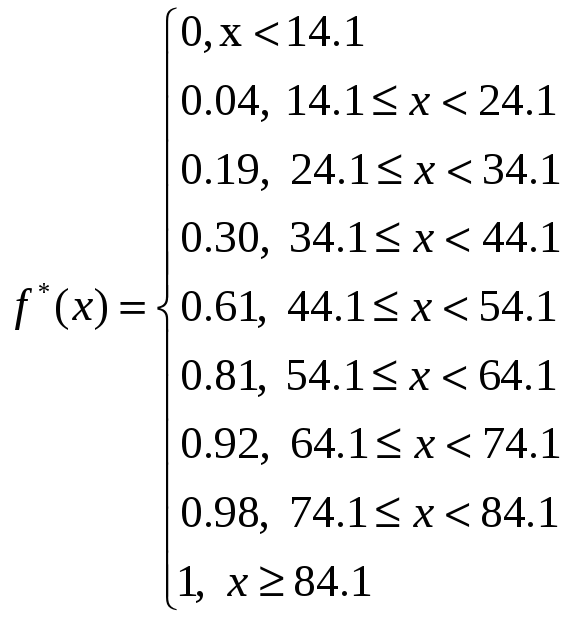Эмпирическая функция распределения
6) Выборочная средняя интервального ряда (несмещенная точечная оценка математического ожидания):
Выборочная дисперсия признака Х:
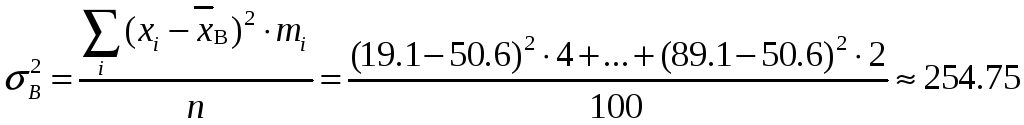
Исправленная дисперсия признака Х:
.
Выборочное СКО признака Х:
.
Исправленное выборочное СКО признака Х:
.
7) Считаем первый столбец таблицы выборкой значений признака Х, а второй – выборкой значений Y. Составим выборочное уравнение прямой регрессии Y на Х.
Выборочное уравнение прямой регрессии:
,
где
,
,
,
,
,
.
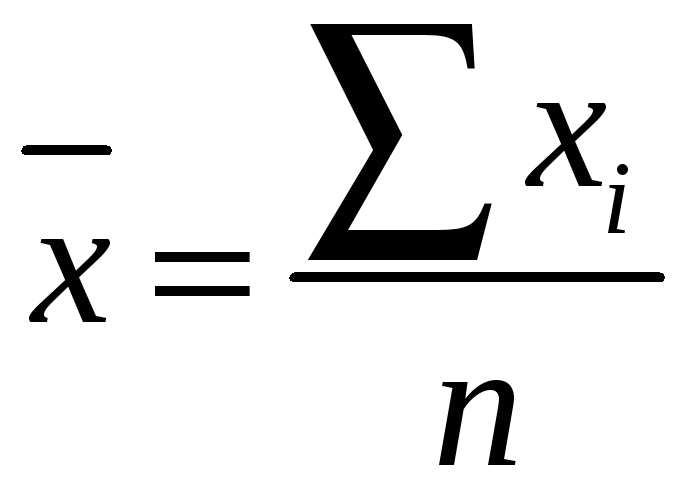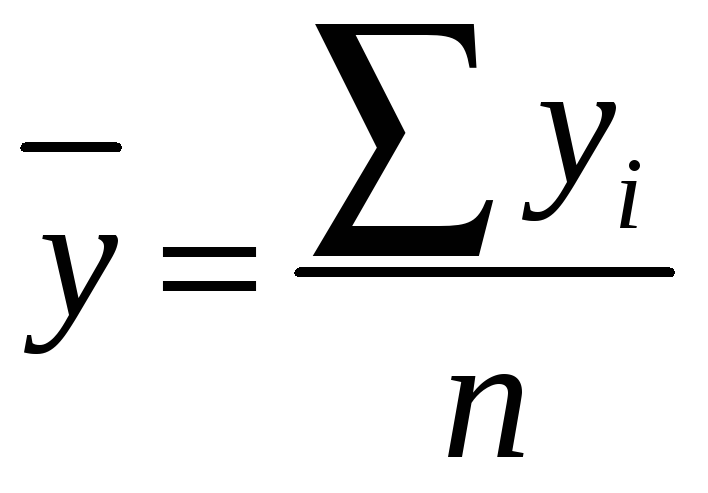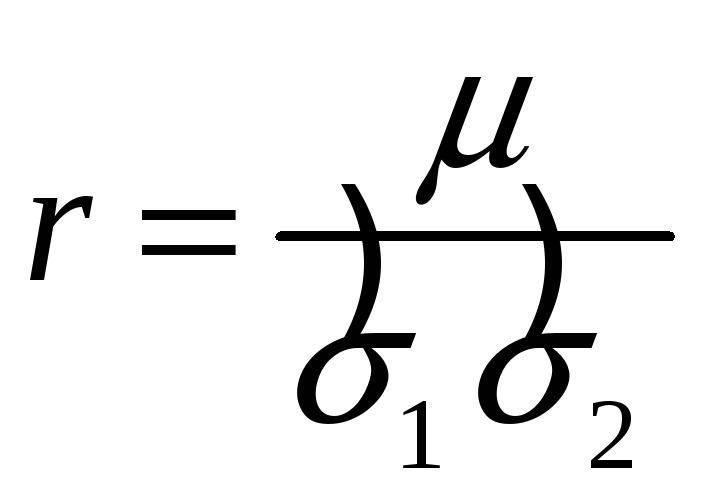Составим таблицу для удобства:
|
xi |
yi |
xi2 |
yi2 |
xi yi |
|
54,3 |
58,1 |
2948,49 |
3375,61 |
3154,83 |
|
14,1 |
25,1 |
198,81 |
630,01 |
353,91 |
|
79,1 |
67,1 |
6256,81 |
4502,41 |
5307,61 |
|
54 |
52,9 |
2916 |
2798,41 |
2856,6 |
|
27,9 |
54,1 |
778,41 |
2926,81 |
1509,39 |
|
55,4 |
62,7 |
3069,16 |
3931,29 |
3473,58 |
|
37,6 |
54,1 |
1413,76 |
2926,81 |
2034,16 |
|
53,6 |
30,8 |
2872,96 |
948,64 |
1650,88 |
|
50,4 |
80,8 |
2540,16 |
6528,64 |
4072,32 |
|
34,2 |
47,9 |
1169,64 |
2294,41 |
1638,18 |
|
460,6 |
533,6 |
24164,2 |
30863,04 |
26051,46 |
Получим:
,
,
,
,
,
,
,
.
Выборочное уравнение регрессии:
Коэффициент корреляции равен r = 0.555, что говорит о прямой и заметной по шкале Чеддока связи между переменными х и y.