
- •1. Метод математической индукции
- •2. Понятие множества, подмножества, пустого множества. Диаграммы Венна. Число подмножеств конечного множества.
- •3. Операции объединения, пересечения множеств, определения и свойства коммутативности и ассоциативности. Взаимная дистрибутивность операций пересечения и объединения.
- •4.Операция вычитания множеств, отсутствие коммутативности и ассоциативности.
- •5.Симметрическая разность, определения и свойства.
- •6.Операция дополнения множеств, принцип двойственности.
- •7. Применение операций объединения, пересечения конечное число раз. Доказательство дистрибутивности и принципа двойственности методом математической индукции.
- •8.Применение операций объединения, пересечения бесконечное число раз. Доказательство дистрибутивности и принципа двойственности для этого случая.
- •9. Разбиение множества, покрытие множества, примеры в математике и информатике.
- •10.Определение слова, подслова, префикса, суффикса, собственного подслова, собственного префикса и суффикса, их свойства. Равенства слов, операции приписывания, свойства операции приписывания.
- •11.Определение кода и основные теоремы о кодах.
- •14. Отношения эквивалентности, порядка, определения, примеры.
1. Метод математической индукции
В математике при доказательстве утверждений часто используется метод математической индукции. Индукция бывает полной и неполной.
Неполная математическая индукция возможно только в том случае, если осуществим полный перебор. Иначе применяют принцип полной математической индукции.
Суть этого принципа состоит в следующем: если некоторое предложение A(n), где n – натуральное число, истинно для n = 1 (или при другом значении n, при котором имеет смысл это утверждение) и из предположения его справедливости для некоторого натурального значения n = k следует справедливость утверждения для следующего натурального значения n = k + 1, то утверждение справедливо для всех натуральных значений n.


Не знаю, писать ли пример?
2. Понятие множества, подмножества, пустого множества. Диаграммы Венна. Число подмножеств конечного множества.
Под множеством понимается некоторая, вполне определенная совокупность объектов или элементов. Множество- любое собрание определенных и различных между собой объектов, мыслимое как единое целое.
Множество А есть подмножество множества, если каждый элемент А есть элемент В\ т.е. если (xпринадлежит А), то (х принадлежит В). В частности, каждое множество есть подмножество самого себя. Таким образом, A не принадлежит В, если существует элемент А, не принадлежащий В.
Пустое множество, обозначаемое перечеркнутый 0 или {}, есть множество, которое не содержит элементов. Универсальное множество U есть множество, обладающее таким свойством, что все рассматриваемые множества являются его подмножествами.
Диаграмма Венна.
Диаграммы Венна —инструмент, позволяющий изображать множества и иллюстрировать операции над ними. Множества в диаграммах Венна изображаются внутренними частями кругов, их пересечениями, объединениями и
т.д. Прямоугольник изображает универсальное множество. На рис. 2.1 приведена диаграмма Венна для множества А которое изображено внутренней частью круга. Внешняя часть круга, находящаяся внутри прямоугольника, изображает А1.
На рис. 2.2 приведена диаграмма Венна для двух множеств, скажем, A и В каждое множество изображено кругом, и круги пересекаются.
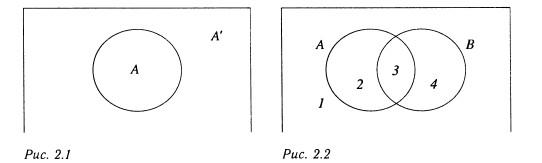
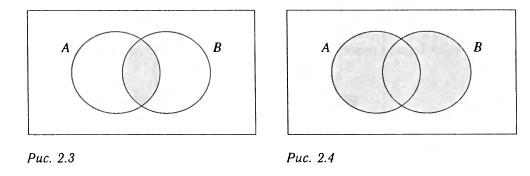
Как показывает диаграмма, внутренняя часть прямоугольника разделена на четыре части. Множеству А и В соответствует закрашенная часть диаграммы на рис. 2.3. Закрашенная область на рис. 2.4 представляет А или В.
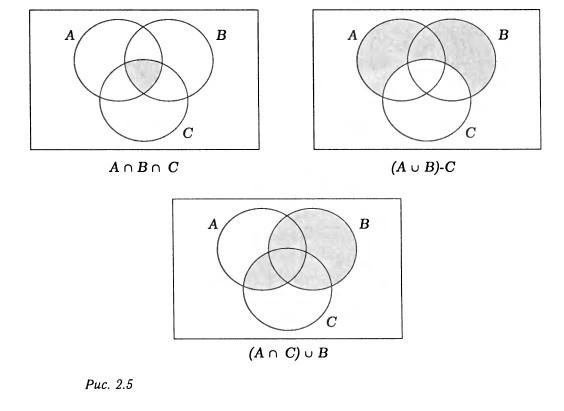
Закрашенные области на рис. 2.5 изображают множества АиВ, (АилиВилиС),
(АиВиС), (АилиВ) —С и (АиС)илиВ. (тут символы были заменены на буквенное обозначение) Множество А-В представлено закрашенной областью на рис. 2.6. Диаграмма Венна для трех множеств, например, А, В и С, показана на рис. 2.7. Эта диаграмма состоит из восьми частей.
Используя диаграммы Венна, можно показать
равенство двух множеств.

Число подмножеств конечного множества
 _____________________________________________________________________________________
_____________________________________________________________________________________
3. Операции объединения, пересечения множеств, определения и свойства коммутативности и ассоциативности. Взаимная дистрибутивность операций пересечения и объединения.
Объединением множеств А и В называется множество, состоящее из всех тех элементов, которые принадлежат хотя бы одному из множеств А или В. Объединение множеств А и В обозначается Аи В. Сформулированное выше определение можно записать так: А и В = {х : х принадлежит А или х принадлежит В}.
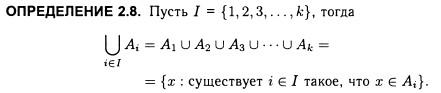

_____________
Если для любых элементов aиbмножестваMсправедливо равенствоab=ba, то операцию называют коммутативной.
Свойство коммутативности: A&B=B&A
A U B=B UA
______________
Если для любых элементов a,b,cмножестваMсправедливо равенствоa(bc)=(ab)c, то операцию называют ассоциативной.
Свойство ассоциативности: A& (B&C) = (A&B) &C
A U (B U C) = (A U B) U C
_______________
Взаимная дистрибутивность операций пересечения и объединения.
Теорема(закон дистрибутивности)

