2. Интерполяция экспериментальных (табличных) данных

2.1 Задание:

1. Представить контур развёртки детали швейного изделия в виде совокупности точек c координатами по осям абсцисс и ординат, сведя их в таблицу.

2. Осуществить интерполяцию контура, представленного со-вокупностью точек, заданной функцией, используя средст-ва MathCad.

3. Дать графическую интерпретацию результатов.

2.2. Постановка задачи интерполяции

На отрезке [a; b] заданы n+1 точки x₀, x₁, x₂,…, x_n-1, x_n

(x₀ < x₁ < x ₂<… < x_{n- 1}< x_n ), называемые узлами интерполяции, и значения некоторой функции f(x) в этих точках, такие что f(x₀) = y₀, f(x₁) = y₁, f(x₂) = y₂,…, f(x_n-1) = y_n-1, f(x_n) = y_n .

Требуется построить такую непрерывную функцию F(x), на-зываемую интерполирующей и принадлежащую к некоторо-му классу функций, которая принимала бы в узлах интерпо-ляции те же значения, что и функция f(x) , т.е. F(x₀) = f(x₀), F(x₁) = f(x₁), F(x₂) = f(x₂),… , F(x_n-1) = f(x_n-1) , F(x_n) = f(x_n).

Процесс вычисления значений функции F(x) называется ин-терполированием.

2.2.1. Интерполяция полиномиальной зависимостью

Для интерполяции используется полиномы вида:

F(x)= a₀ + a₁x + a₂x² + … + a_n-1x^n-1 + a_nxⁿ ,

где коэффициенты a₀, a₁, a₂, …– корни системы линейных алгебраических уравнений:

1 x0 x0^2x0^3… x0^n-1x0^n 1 x1 x1^2x1^3… x1^n-1x1^n 1 x2 x2^2x2^3… x2^n-1x2^n … ……………………….. ………………………….. 1 xn xn^2xn^3… xn^n-1xn^n

∙

a0 a1 a2 . . an

=

y0 y1 y2 . . yn

В этом уравнении x_0, x_1, x₂, …, x_n и y_0, y_1, y₂, …, y_n значения координат n+1 точки контура, отложенные соответственно по осям абсцисс и ординат.

2.2.2. Использование встроенных функций MathCad

Для решения задач интерполяции могут использоваться сле-дующие функции MathCad:

1) linterp(X,Y,x) – функция, интерполирующая точки контура кусочно-линейной зависимостью.

2) interp(S,X,Y,x)- функция, интерполирующая точки контура сплайнами.

S – вектор значений коэффициентов соответствующих сплайнов, вычисляемых с помощью одной из функций:

● lspline(X,Y)- для линейных сплайнов;

● pspline(X,Y) - для квадратичных сплайнов;

● cspline(X,Y) –для кубических сплайнов.

X и Y – векторы-столбцы, элементы которых определяют зна-чения координат точек соответственно по осям абсцисс и ординат. x – значение аргумента при котором вычисляется интерполирующая функция.

2.3. Примеры

В рассматриваемых примерах значения координат точек даны в сантиметрах.

2.3.1. Для криволинейного контура развёртки оката рукава, заданного координатами точек по осям абсцисс и ординат соответственно x, у

x	-15	-14	-13	-8,2	-3	0	3	7,4	11	13	15
y	0,5	0,7	1,2	6	10,2	10,8	10	6	1,5	0,5	0

осуществить интерполяцию квадратичными сплайнами.

Решение задачи в среде MathCad.

Исходные данные – координаты точек из приведённой таб-лицы задаём как векторы-столбцы, предварительно задав начальные значения индексов:

ORIGIN :=0

Вектор коэффициентов квадратичного сплайна cs и интер-поляционная сплайн-функция F(x)имеют вид:

ps:= cspline(X,Y) F(x):=interp(ps, X, Y, x)

Начальные, конечные значения, шаг изменения аргумента x, при котором вычисляется интерполирующая функция F(x), и сам аргумент х задаём в виде:

x0:=X₀ xk:=X₁₀ Δx:=0.1 x:= x0,x0+Δx..xk

После этого строим график, на который выводим исходные точки (заданные векторами X и Y) и значения функции F(x).

На графике символами ○ обозначены исходные точки, сплошной линией – значения интерполирующей функции.

2.3.2. Осуществить интерполяцию полиномиальной зави-симостью контура фигурного входа в карман, заданного точками с координатами по оси абсцисс x и оси ординат y:

x	0	0,85	3	6	8,6	10,7	13
y	7	6	4	2,5	2,1	2,1	2,6

Для 7-ми точек полиномиальная интерполирующая функция имеет вид: F(x)= a₀ + a₁x + a₂x² + a₃x³ + a₄x⁴ + a₅x⁵ + a₆x⁶. Коэффициенты a₀, a₁, a₂, …, a₆ являются корнями системы линейных алгебраических уравнений: L∙A = Y, где

L=

1 x0 x0^2x0^3x0^4 x0^5x0^6 1 x1 x1^2x1^3x1^4x1^5 x1^6 1 x2 x2^2x2^3x2^4x2^5x2^6 1 x3 x3^2x3^3x3^4x3^5x3^6 1 x4 x4^2x4^3x4^4x4^5x4^6 1 x5 x5^2x5^3x5^4x5^5x5^6 1 x6 x6^2x6^3x6^4x6^5x6^6

А=

a0 a1 a2 a3 a4 a5 a6

Y=

y0 y1 y2 y3 y4 y5 y6

Решение задачи в среде MathCad: ORIGIN :=0

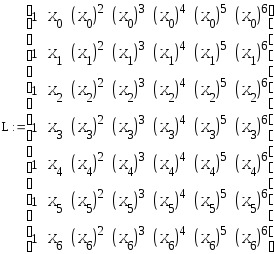
Элементы матрицы L можно вычислить более удобным способом, используя циклы: i :=0..5 j :=0..5 L_i,j :=X_i^j

Систему уравнений решаем с помощью функции lsolve:

A:=lsolve(L,Y)

Функцию F(x) задаём в виде:

x0:= X₀ xk:=X₁₀ Δx:=0.1

x:= x0,x0+Δx..xk

Исходные точки и значения интерполирующей функции

выводим на график:

2.3.3. На рис. 2.3 показан фрагмент развёртки клапана кар-мана.

Рис. 2.3. Контур развёртки клапана кармана.

На рис. 2.3 засечками, пронумерованными числами 1..22, обозначены номера точек контура с координатами x_i, y_i, i=1..22.

Контур развёртки представляет собой кривую линию, у кото-

рой одному значению, отложенному по оси абсцисс, может соответствовать несколько значений на оси ординат.

В этом случае вместо интерполирующей функции F(x ) ис-пользуют параметрические интерполирующие функции x(t) и y(t). t - параметр, в нашем случае 1 ≤ t ≤ 22; 1, 2,3, .. 22 – но-мера точек на рис. 2.3.

Функции x(t), y(t), будучи отложенны-ми на графике соответственно по осям абсцисс и ординат, отображают криволинейный контур развёртки клапана кар-мана.

Решение задачи в среде MathCad на примере интерполяции кубическими сплайнами.

Исходными данными будут три

вектора- столбца:

● вектор N – номера точек, взятые

по порядку;

● векторы X и Y –значения коор-динат точек соответственно по осям абсцисс и ординат.

ORIGIN :=0

Векторы коэффициентов сплайнов sx, sy и параметрические интерпо-

ляционные сплайн-функции x(t), y(t)имеют вид:

sx:=cspline(N,X)

sy:= cspline(N,Y)

x(t):=interp(sx, N, X, t)

y(t):=interp(sy, N, Y, t)

Начальные, конечные значения, шаг изменения аргумента t, при котором вычисляется интерполирующая функция, и сам аргумент t задаются следующим образом:

t0:=N₀ tk:=N₂₁ Δt:=0.1 t:= t0,t0+Δt..tk

После этого на график выводятся исходные точки (задан-ные векторами X и Y) и значения функций x(t)и y(t) со-ответственно по осям абсцисс и ординат:

2.3.4. Фрагмент контура развёртки проймы спинки предс-тавляет собой кривую линию, у которой, как и предыду-

щем случае, одному значению, отложенному по оси абс-

цисс, соответствует несколько значений на оси ординат. Контур задан экспериментальными точками:

N	1	2	3	4	5	6
x	3,4	2,4	1,8	2,1	3,4	5,8
y	14,2	10,7	7,5	4,0	0,7	-1,7

Для интерполяции полиномиальной зависимостью исполь-зуются параметрические функции:

x(t)= a_{x 0} + a_{x 1}t+ a_{x 2}t² + a_{x 3}t³ + a_{x 4}t⁴ + a_{x 5}t⁵

y(t)= a _{y 0} + a_{y 1}t + a_{y 2}t² + a_{y 3}t³ + a_{y 4}t⁴ + a_{y 5}t⁵,

1≤ t ≤ 6; 1 2, .. 6 – номера экспериментальных точек контура.

Коэффициенты a _{x 0}, a _{x 1}, …, a _{x 5}, a _{y 0}, a _{y 1}, …, a _{y 5} определяются из решения двух систем алгебраических уравнений: L∙Ax = X и L∙Aу =Y

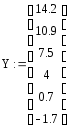
Решение: ORIGIN:=0

Вычисляем элементы матрицы L:

i :=0..5 j :=0..5 L_i,j :=N_i^j

Корни линейных алгебраических уравнений вычисляем

методом обратной матрицы:

Затем вычисляем значения t и строим график:

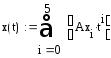
t0:=N₀ tk:=N₅ Δt:=0.02 t:=t0,t0+Δt..tk

2.3.5. Контур развёртки нижнего воротника из ткани, представляющий собой замкнутую кривую линию, задан совокупностью точек.

Нумерацию точек контура будем осуществлять по поряд-

ку по направлению часовой стрелки.

При этом начальная и конечная точки контура должны

совпасть (иметь одни и те же значения координат).

В рассматриваемом примере – это точки 1 и 19.

Решение задачи в среде MathCad на примере интерполя-ции кусочно-линейной зависимостью:

ORIGIN :=0

Параметрические интерполяционные функции имеют вид:

x(t):=linterp(N, X, t) y(t):=linterp(N, Y, t)

Вычисляем значения t :

t0:=N₀

tk:=Nk

Δt:=0.02

t:=t0,t0+Δt..tk

и строим график: