
- •Глава 3. Линии и поверхности второго порядка
- •§1. Исследование уравнения кривой второго порядка
- •§2. Эллипс
- •§ 3. Гипербола
- •§4. Директрисы эллипса и гиперболы
- •§5. Парабола
- •§ 6. Краткое описание различных видов поверхностей второго порядка
- •Двуполостный гиперболоид вращения– это поверхность вращения гиперболы
- •§ 7. Примеры решения типовых задач
- •Вопросы для самопроверки
Глава 3. Линии и поверхности второго порядка
§1. Исследование уравнения кривой второго порядка
Линию второго порядка на плоскости в общем виде можно задать с помощью уравнения:
Ax2 + 2Bxy + Cy2 + 2Dx + 2Ey + F = 0,
в котором коэффициенты А,ВиСне равны нулю одновременно. Систему координат будем предполагать декартовой прямоугольной.
Предположим, что коэффициент В ≠ 0. Для того чтобы упростить общее уравнение, совершим поворот декартовой прямоугольной системы координат на угол φ вокруг начала координат. Старые координаты x и y будут связаны с новыми координатами x′, y′ формулами перехода:
x = x′cosφ – y′sinφ,
y = y′sinφ + y′cosφ.
В новых координатах уравнение примет вид
A(x′cosφ – y′sinφ)2 + 2B(x′cosφ – y′sinφ)( y′sinφ + y′cosφ) +
+ C(y′sinφ + y′cosφ)2 + 2D(x′cosφ – y′sinφ) + 2E(y′sinφ + y′cosφ) + F = 0.
Выпишем коэффициент, получающийся после раскрытия скобок и приведения подобных членов при произведении x′y′:
B′ = –2Acosφ sinφ – 2Bsin2φ + 2Bcos2φ + 2Csinφ cosφ.
Выберем угол φ таким образом, чтобы B′ был равен нулю:
B′ = (C – A)2cosφ sinφ + 2B(cos2φ – sin2φ) = 0
или
2Bcos2φ = (A – C)sin2φ.
Если
А
= С,
то в качестве угла поворота φ можно
положить
![]() .
ЕслиА
≠ С,
то получаем
.
ЕслиА
≠ С,
то получаем
![]() и угол
и угол![]() .
Важно, что такой угол существует, и после
поворота системы координат на этот угол
рассматриваемое уравнение заменяется
на уравнение
.
Важно, что такой угол существует, и после
поворота системы координат на этот угол
рассматриваемое уравнение заменяется
на уравнение
A′x′2 + C′y′2 + 2D′x′ + 2E′y′ + F ′ = 0.
Если в это уравнение входит с ненулевым коэффициентом квадрат одной из координат, то при помощи переноса начала координат вдоль соответствующей оси, можно обратить в нуль член с первой степенью этой координаты.
В самом деле, пусть, например, A′ ≠ 0. Перепишем уравнение в виде
A′(x′2
+
![]() x′)
+ C′y′2
+ 2E′y′
+ F
′ = 0.
x′)
+ C′y′2
+ 2E′y′
+ F
′ = 0.
Дополним выражение в скобках до полного квадрата, получим
A′ –
–![]() +C′y′2
+ 2E′y′
+ F
′
= 0
+C′y′2
+ 2E′y′
+ F
′
= 0
или
A′![]() + C′y′2
+ 2E′y′
+ F
′ –
+ C′y′2
+ 2E′y′
+ F
′ –
![]() = 0.
= 0.
Если мы сделаем перенос начала координат, определенный формулами
x′′
= x′
+
![]() ,
,
y′′ = y′,
то уравнение примет вид
A′x′′2 + C′y′′2 + 2E′y′′ + F′′ = 0.
Если С′ ≠ 0, то выделяем полный квадрат со слагаемыми, содержащими y′′ и, делая перенос начала координат вдоль оси Oy, получим еще более упрощенное уравнение.
Рассматривая в упрощенных уравнениях различные комбинации знаков коэффициентов, приходим к следующей теореме.
Теорема. Пусть в декартовой системе координат задано уравнение второго порядка
Ax2 + 2Bxy + Cy2 + 2Dx + 2Ey + F = 0.
Тогда существует такая декартова прямоугольная система координат, в которой это уравнение принимает один из девяти канонических видов:
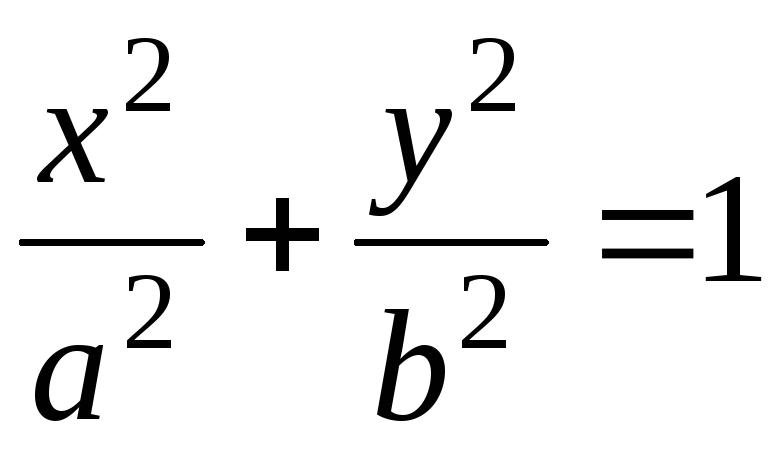 –уравнение
эллипса;
–уравнение
эллипса;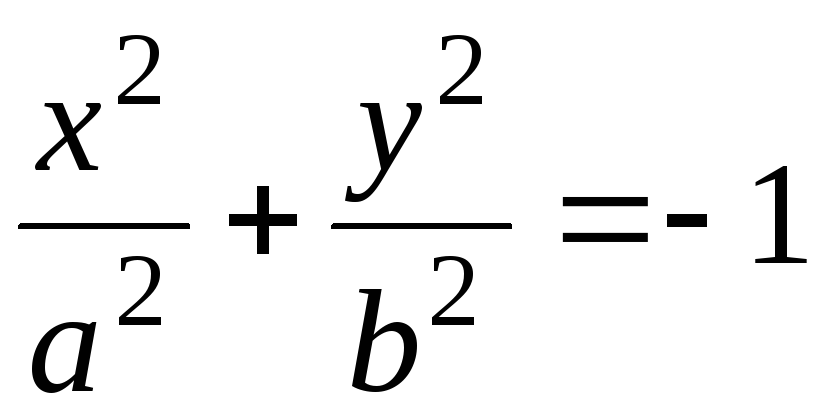 –уравнение
мнимого эллипса;
–уравнение
мнимого эллипса;a2x2 + c2y2 = 0 – уравнение пары мнимых пересекающихся прямых;
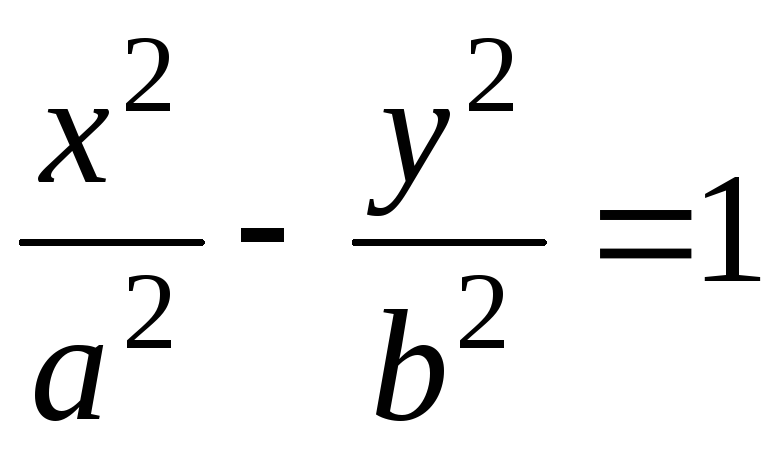 –уравнение
гиперболы;
–уравнение
гиперболы;a2x2 – c2y2 = 0 – уравнение пары пересекающихся прямых;
y2 = 2px – уравнение параболы;
y2 – a2 = 0 – уравнение пары параллельных прямых;
y2 + a2 = 0 – уравнение пары мнимых параллельных прямых;
y2 = 0 – уравнение пары совпавших прямых.
Заметим, что уравнению мнимого эллипса и уравнению пары мнимых параллельных прямых не удовлетворяет ни одна точка на действительной плоскости.
Собственно линиями второго порядка являются эллипс,гипербола,парабола. Другие случаи линий второго порядка называютсявырожденными. Окружность рассматривается как частный случай эллипса.
В следующих параграфах подробнее остановимся на невырожденных случаях кривых второго порядка, которые определим через их геометрические свойства и покажем, что линии с этими свойствами сводятся к перечисленным в теореме уравнениям.
