−

1.ФИЗИЧЕСКИЕ ОСНОВЫ МЕХАНИКИ

1.1.КИНЕМАТИКА МАТЕРИАЛЬНОЙ ТОЧКИ

1.1.1.Общие понятия механики.

Механика – раздел физики, который рассматривает простейшую форму движения материи – механическое движение.

Под механическим движением понимают изменение положения изучаемого тела в пространстве со временем относительно некоторого тела или системы тел, условно считаемых неподвижными. Такую систему тел вместе с часами, в качестве которых может быть выбран любой периодический процесс, называют системой отсчета. Систему отсчета часто выбирают из соображений удобства. Для математического описания движения с системой отсчета связывают систему координат, часто прямоугольную.

Простейшее тело в механике – материальная точка. Это тело, размерами которого в условиях данной задачи можно пренебречь.

Всякое тело, размерами которого пренебречь нельзя, рассматривают как систему материальных точек.

Механика подразделяется на кинематику, динамику и статику. Кинематика занимается геометрическим описанием движения, не изучая его причин. Динамика изучает законы движения тел под действием сил. Статика изучает условия равновесия тел.

	1.1.2. Кинематика точки
	Кинематика изучает пространствен-			r12 = r2 – r1 = r
	но-временное перемещение тел. Она опе-	z
	рирует такими понятиями, как переме-		1	2
	щение r, путь S, время t, скорость	r1
	движения V, ускорение a.			r2
	Линию, которую описывает при сво-
				x
	ем движении материальная точка, назы-
	вают траекторией. По форме траектории	y
	движения делятся на прямолинейные и	Рис. 1.1.1
	криволинейные. Вектор r12, соединяю-
	щий начальную 1 и конечную 2 точки,

называют перемещением (рис. 1.1).

Каждому моменту времени t соответствует свой радиус-вектор r(t): r(t) = x2 + y2 + z2 .

Таким образом, движение точки может быть описано векторной функцией
r(t)= x(t)i + y(t)j + z(t)k ,	(1.1.1)

которая определяет векторный способ задания движения, или тремя скалярными функциями

	−
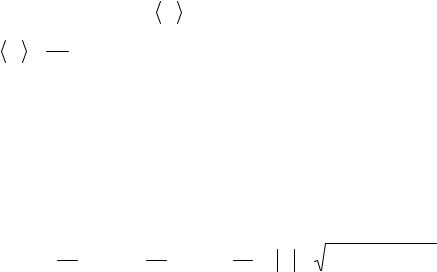
x = x(t); y = y(t); z = z(t),	(1.1.2)

которые называют кинематическими уравнениями. Они определяют задание движения координатным способом.

Движение точки будет также определено, если для каждого момента вре-

мени будет установлено положение точки на траектории, т.е. зависимость
S = f (t).	(1.1.3)

Она определяет задание движения естественным способом.

Каждая из указанных формул представляет собой кинематический закон движения точки.

1.1.3.	Скорость
Если моменту времени					t1	соответствует радиус-вектор r1, а	t2 – r2, то за
промежуток		t = t2 − t1		тело получит перемещение r = r2 −r1.			В этом слу-
чае средней скоростью				V	за	t называют величину
V =	r ,						(1.1.4)
	t
которая по отношению к траектории представляет секущую, проходящую
через точки 1		и 2. Скоростью в момент времени t называют вектор
V = lim		r	= dr .				(1.1.5)
t→0		t	dt

Из этого определения следует, что скорость в каждой точке траектории направлена по касательной к ней. Из (1.1.5) следует, что проекции и модуль вектора скорости определяются выражениями:

V = dx		;	V	= dy ;	V	= dz ; V =	V2	+ V2	+ V2 .	(1.1.6)
X	dt		Y	dt	Z	dt	X	Y	Z

Если задан кинематический закон движения (1.3), то модуль вектора скорости определится так:

V

= V =

lim

r

= lim

r

= lim

S

= dS

(1.1.7)

t→0

t

t→0

t

t→0

t

dt

Таким образом, зная закон движения (1.1.1), (1.1.2), (1.1.3) можно вычислить вектор и модуль вектора скорости и, наоборот, зная скорость из формул (1.1.6), (1.1.7), можно вычислять координаты и путь.

1.1.4. Ускорение

При произвольном движении вектор скорости непрерывно меняется. Величина, характеризующая быстроту изменения вектора скорости, называется ускорением a.

Если в момент времени t1 скорость точки V1, а при t2 – V2, то приращение скорости составит V = V2 − V1 (рис. 1.1.2). Среднее ускорение при

этом

								−
a =			Vt ,					(1.1.8)
а мгновенное
a =	dV			=	d2r
							.	(1.1.9)
		dt			dt	2

Для проекций и модуля ускорений имеем:

ax =	dV	d2x		; ay =	dV	d2y		; az =	dV	d2z	;
	x =		2		x =		2		zx =	dt2
	dt	dt			dt	dt			dt		(1.1.10)

a = a22 + a2y + a2z

Если задан естественный способ движения, то ускорение можно определить и так. Скорость меняется по величине и по направлению, приращение скорости

V	раскладывают	на	две	величины:
Vτ − направленный вдоль		V (приращение скорости

по величине) и Vn – направленный перпендикулярно

	α	V1
		V
		V2
		V2
		Рис. 1.1.2

V (приращение		скорости	по направлению), т.е.		V1	Vτ
V = Vτ +	Vn	(рис. 1.3).		M
					α	p
a = dVτ	+ dVn		(1.1.11)				N
				R		V
dt	dt
aτ = dVτ .			(1.1.12)	α		0
dt							V2
Тангенциальное (касательное) ускорение харак-
теризует быстроту изменения V по величине.					Рис. 1.1.3
an = dVn ,			(1.1.13)
dt
нормальное (центростремительное ускорение) характеризует быстроту из-
менения V по направлению. Для вычисления an				рассмотрим		0MN и MP0

при условии малого перемещения точки по траектории. Из подобия этих треугольников находим P0:MP = MN:0M

V

S

V

dV

V2

n =

V

=

S;

a

n

=

n

=

.

(1.1.14)

V

R

n

R

dt

R

Полное ускорение в этом случае определится так:

a = a

2

+ a2

=

dV 2

V2

2

(1.1.15)

+

.

τ

n

dt

R

1.1.5. Примеры

Равнопеременное прямолинейное движение. Это движение с постоянным ускорением (a = const). Из (1.1.8) находим