II. Экспериментальный раздел работы

Пример 1. Вычисление факториала. Факториал числа n! определяет количество способов размещения n предметов в некотором ряду. Так, при n=3 имеется три способа для размещения первого предмета. Если он уже зафиксирован, то существует два способа установки второго предмета и один для третьего. Таким образом, 3!=3*2*1=6. Приведем таблицу для нескольких первых значений факториала: 4!=24; 5!=120; 6!=720; 7!=5040; 8!=40320 … Характерной особенностью этой величины является ее экспоненциальное возрастание. При больших значениях n справедлива следующая оценка Стирлинга:

. (2)

Некоторые важные свойства факториала можно найти в справочной литературе, а мы подробнее остановимся на рекурсивном алгоритме его вычисления. Запишем факториал в виде

n! = n (n-1)! (3)

В такой записи задача вычисления факториала сводится к ней самой же, путем изменения исходных данных, т.е. «новое» значение n! выражено через «старое» (n-1)!. Кроме того, условие 0! =1 позволяет завершить вычислительный процесс. Составим рекурсивную функцию:

double Factorial(int number)

{

if (number > 1)

return number * Factorial(number - 1);

return 1;

}

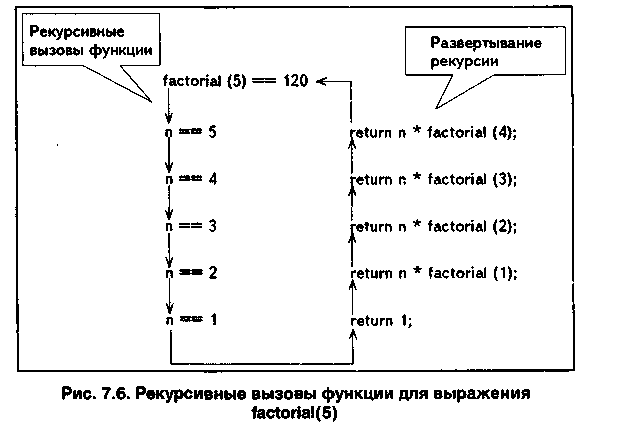
Рис 1. Рекурсивные вызовы функции для выражения factorial(5).

Пример 2. Алгоритм Евклида. Построим рекурсивные алгоритмы вычисления наибольшего общего делителя НОД (n,m) двух целых чисел n и m. Говорят, что два целых числа делятся (или n кратно m), если n=k*m, где k – целое число. Наибольший общий делитель – это максимальное значение числа k, которое делит и n и m. Например,

НОД (39, 15)=3, НОД (18, 12)=6.

Геометрическая трактовка НОД (n, m) – это набольшая общая мера двух соизмеримых отрезков, т.е. отрезков, каждый из которых в n и m-раз соответственно длиннее, чем некоторый выбранный отрезок - масштаб. Такая геометрическая иллюстрация НОД подсказывает простейший, буквально следующий определению, алгоритм его нахождения. Действительно, выберем из двух отрезков наименьший и проверим, не укладывается ли он целое число раз в другом. Если да, то цель достигнута. Если нет, то возьмем половину меньшего отрезка и проверим, не укладывается ли он целое число раз в другом. В случае неудачи перейдем к трети отрезка и т.д. Условие соизмеримости отрезков гарантирует успешное окончание этого процесса. Представим описанный алгоритм в виде подпрограммы-функции

int Nod(int n,int m)

{

int i,k,rez;

if(n>m) k=m;

else k=n;

for(i=1;i<=k;i++){

if((m%i==0)&&(n%i==0)) rez=i;}

return rez;

}

Нетрудно заметить, что такой алгоритм неэффективен, поскольку предполагает выполнение многих лишних действий по перебору нужного варианта (при n>m необходимо выполнить m - действий). Существенно более выгодным является метод, предложенный Евклидом более 2300 лет назад. Рассмотрим две его трактовки в связи с возможностью их рекурсивной реализации. Алгоритм Евклида строится, опираясь на свойства наибольшего общего делителя. Сформулируем их:

1. НОД (n, m) = НОД (-n, m) = НОД (n,-m);

2. НОД (n, m) = НОД (n - m, m) = НОД (n, m - n);

3. НОД (n, 0) = n, при n 0;

4. НОД (n, m) = НОД ( m, n mod m);

В записи этих свойств уже заложена рекурсивная трактовка. Рассмотрим сначала более подробно свойства 3 и 4. Пусть a₀ = n, а₁= m. Основываясь на указанных свойствах можно сформировать последовательность остатков от деления а₂, а₃,…, используя рекуррентное соотношение

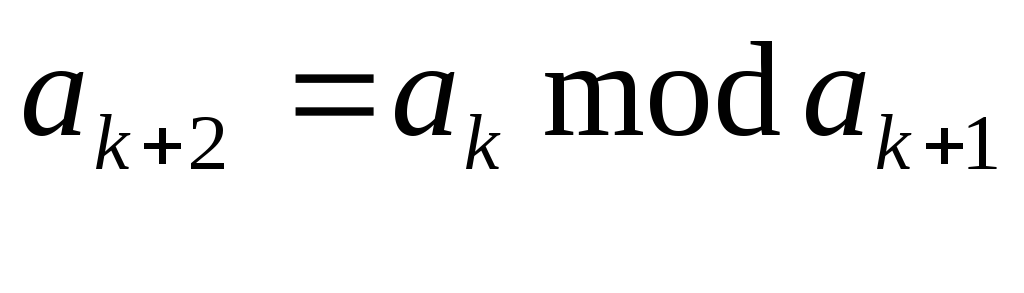(4)

Продолжая этот процесс до тех пор, пока a_n+1 =0, получим

НОД (a₀,a₁) = НОД (a₁,a₂) = …= НОД (a_n,0) = a_n (5)

Данную последовательность можно записать в более привычном виде:

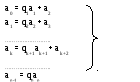
где q_k - целые числа.

Например,

НОД (39,15) = НОД (15,9) = НОД (9,6) = НОД (6,3) = НОД (3,0) = 3

Действительно, разложив на множители эти числа 39 = 3*13 и 15 = 3*5, получим

НОД (39,15)= 3.

Поскольку нет необходимости запоминать промежуточные результаты и, следовательно, вводить массив целых чисел, запишем алгоритм Евклида так:

1. Ввод исходных данных: n,m;

2. Повторить r = n mod m; n = m; m = r пока r = 0;

3. Вывод результата: НОД (n,m) = n.

Составим подпрограмму-функцию:

int Nod_2(int n,int m)

{

int r=n%m;

if(r==0) return m;

else return Nod_2 (m,r);

}

Составьте подпрограммы вычисления НОД на основе свойств 1 и 2.

Настоятельно рекомендуется поэкспериментировать с приведенными функциями, сравнить их по количеству действий, эффективности действий, наглядности и т.д.

Пример 3. Решение нелинейных уравнений. Рассмотрим задачу нахождения корней нелинейного уравнения

f(x)=0 (6)

Алгоритм нахождения корней приближенными методами можно разбить на два этапа. На первом – изучается расположение корней и проводится их разделение. Находится область [a,b], в которой существует корень уравнения или начальное приближение к корню x₀. Простейший способ выделения корней – табуляция функции и анализ ее графика.

Существование на найденном отрезке [a,b], по крайней мере, одного корня уравнения (6) следует из условия, что знаки функций на концах отрезка различны:

f(a) ∙ f(b) < 0 (7)

При этом подразумевается, что функция f(x) непрерывна и монотонна на данном отрезке

На втором этапе решения, используя полученное начальное приближение, стоится итерационный процесс, позволяющий уточнять значение корня с некоторой, наперед заданной точностью .

(8)

Рассмотрим простейший метод уточнения значения корня с заданной точностью - метод деления отрезка пополам. Если определен интервал нахождения корня [a,b], то этот алгоритм состоит из:

1. Задания значений величин и вычисления значений функции u=f(a), v:=f(b).

2. Последовательно выбранный отрезок делится пополам и осуществляется выбор того из двух отрезков, на котором функция меняет знак.

3. Вычисление заканчивается, если выполнено условие (8), иначе возврат к шагу 2.

Приведем рекурсивный вариант программы-функции, реализующей описанный метод:

double X_Dich(double a, double b, double eps){

double x;

if (f(a)*f(b)> 0.0) {cout<<”error”};exit;}

else

{ x=0.5*(a+b);

if (abs(f(x)) > eps)

{ if (f(a)*f(x) <0.0)

Return X_Dich(a,x,eps);

Else Return X_Dich(x,b,eps);

Return x;

}

}

Изучите приведенный алгоритм, проведите отладку программы и сделайте её тестирование. В качестве теста используйте любое уравнение с известным решением. В частности, можно рекомендовать уравнение Валлиса , имеющего один вещественный корень 2.09455.

Полезно в своей библиотеке иметь не только подпрограммы-функции, но и процедуры, составленные на основе приведенных алгоритмов. Напишите их, выполните отладку и тестирование. Составьте подпрограммы с использованием рекурсии и без нее.

Выбор очередной точки в середине отрезка не является единственным вариантом. Можно в качестве такой точки выбрать случайное число, заменив оператор x:=0.5*(a+b) на x:=a+(b-a)*random, предварительно инициализируя датчик случайных чисел Randomize. Проведите соответствующие расчеты и сравните требуемое число итераций для достижения заданной точности.

Более совершенный метод выбора точки деления отрезка [a,b] – метод хорд, в котором в качестве x выбирается точка пересечения с осью абсцисс прямой y=Ax+B (хорды), проведенной через концы интервала u=f(a) и v=f(b).

, где . (9)

Сделайте корректировку программы и проведите вычислительный эксперимент, сравнивая число итераций, требуемых для достижения заданной точности.

Определите количество итераций разных методов, требуемых для достижения точности .

Детальнее проанализировав этот алгоритм, нетрудно заметить, что выполняются лишние действия. Действительно, когда проводится повторный расчет с уменьшенным вдвое шагом, происходит повторное вычисление значений функции в некоторых из узлов.

Проведите экспериментальные расчеты и проанализируйте их.

Пример 5. Рассмотрим рекуррентную числовую последовательность Фибоначчи, играющую важную роль в математике:

f(0) = 0; f (1) = 1

f (n) = f (n-1) + f (n-2), (12)

Запишем несколько первых значений последовательности чисел Фибоначчи:

f(2)=1; f(3)=2; f(4)=3; f(5)=5; f(6)=8; f(7)=13;…..

Простейшее рекуррентное соотношение второго порядка (12), в котором каждое следующее значение вычисляется по двум предыдущим, может быть естественным образом реализовано в виде рекурсивной функции:

int Fib(int n){

if (n= = Ø) return Ø;

if (n = = 1) return 1;

else return Fib(n – 2) + Fib(n-1)

}

Приведем не рекурсивный вариант решения данной задачи:

int Fib(int n){

int i,j,k,m;

m=Ø; k=1;

for(i=2; i<=n; i++){

j=k;

k+=m;

m=j;

end;

return k;

}

Сравнение этих подпрограмм показывает, что рекурсивный вариант организован не лучшим образом, он менее экономичен по числу обращений к функции. Это и понятно, вычисление слагаемого f(n) требует ссылки на f(n-1) и f(n-2). А вычисление слагаемого f(n-1), в свою очередь, на f(n-2) и f(n-3), т.е. происходит два независимых вычисления f(n-2). Это можно проиллюстрировать в виде следующего дерева графа для n = 4:

4

3 2

1 0

2 1

Из девяти вызовов функции f(n) - четыре сделаны повторно. Это неэффективно.

Приведем аналитическое решение рекуррентного соотношения (6):

(13)

Нетрудно показать, что вычисление по рекурсивному алгоритму требует обращений к функции, в отличие от N₁ = (n – 2) обращений во второй программе, использующей цикл. Зависимость N₁ от n - линейная, а N₂ от n - показательная с основанием , т.е. .

Данный пример показывает неудачное применение рекурсии и указывает на необходимость тщательного анализа используемых алгоритмов. Красиво не всегда означает эффективно. Кстати и циклические вычисления не застрахованы от плохой реализации, где могут, например, повторяться уже проделанные операции. Но, как правило, итерационные алгоритмы более прозрачны с точки зрения их анализа, в отличие от рекурсивных, где заметить дефекты бывает значительно труднее. Несмотря на сказанное, рекурсия это мощный инструментарий, позволяющий легко реализовывать многие сложные алгоритмы. Но об этом еще разговор впереди, а сейчас нужно освоить простейшие навыки составления рекурсивных подпрограмм.