
- •Глава 6. Неопределённый интеграл
- •Задачи для самостоятельного решения
- •6.5 Интегрирование простейших функций, содержащих квадратный трехчлен.
- •Задачи для самостоятельного решения
- •6.6. Рациональные дроби
- •6.7 Интегрирование простейших рациональных дробей
- •6.8 Интегрирование рациональных дробей
- •Задачи для самостоятельного решения
- •6.9 Интегрирование некоторых тригонометрических функций.
- •Задачи для самостоятельного решения
- •6.10 Интегрирование некоторых иррациональных функций.
- •Задачи для самостоятельного решения
- •Ответы к задачам главы 6:
Задачи для самостоятельного решения
72.![]() .
73.
.
73.![]() .
74.
.
74.![]() .
75.
.
75.![]() .
76.
.
76.![]() .
77.
.
77.![]() .
.
78![]() .
79.
.
79.![]() .
80.
.
80.![]() .
81.
.
81.![]() .
82.
.
82.![]() .
83.
.
83.![]() .
.
84.![]() .
85.
.
85.![]() .
86.
.
86.![]() .
87.
.
87.![]() .
88.
.
88.![]() .
89.
.
89.![]() .
.
90.![]() .
91.
.
91.![]() .
92.
.
92.![]() .
93.
.
93.![]() .
.
6.9 Интегрирование некоторых тригонометрических функций.
 .
(9.1)
.
(9.1)
Интеграл всегда берется в конечном виде
подстановкой
![]() .
.
![]() .
.
Эта подстановка является универсальной
для интегралов (9.1). Особенно удобно ею
пользоваться, если под интегралом стоит
дробь, в числителе и знаменателе каждой
стоят многочлены относительно
![]() и
и![]() ,
степени не более первой.
,
степени не более первой.
Пример.Найти интеграл![]() .
.
Сделаем подстановку
![]() .
. =
=
![]()
![]() .
.
Заметим, что подстановка
![]() ,
приводит иной раз к сложным выкладкам.
Ниже указаны случаи, когда цель может
быть достигнута с помощью более простых
подстановок.
,
приводит иной раз к сложным выкладкам.
Ниже указаны случаи, когда цель может
быть достигнута с помощью более простых
подстановок.
 .
.
Если имеет место тождество
![]() ,
то удобнее сделать подстановку
,
то удобнее сделать подстановку![]() ,
,![]() .
.
Пример.Найти интеграл![]() .
.
Т.к.![]() ,
,
то делаем подстановку
![]() ,
тогда
,
тогда ;
;![]() ;
;
![]() ;
; .
.
=
![]()
=![]()
![]() =
=
 .
.
3)![]() . Для нахождения этих интегралов
применяется подстановка
. Для нахождения этих интегралов
применяется подстановка
![]() .
.
![]() . Подстановка
. Подстановка![]()
Пример.Найти интеграл![]()
Сделаем подстановку
![]()
![]() #
#
4)
![]() ,
,
![]()
Интеграл берётся понижением степени
![]() с помощью формул
с помощью формул![]() ;
;![]()
Пример.Найти интеграл![]() .
.
![]()
![]()
 .
.
5)![]() .
Хотя бы одно из чисел
.
Хотя бы одно из чисел![]() – целое положительное нечетное. Например,
– целое положительное нечетное. Например,![]() .
.![]()
![]()
![]() .
.
Дальше можно сделать подстановку
![]() .
.
Пример.Найти интеграл![]() .
.
![]()
![]()
6) Интегралы вида
![]()
Подынтегральные выражения преобразуются в сумму тригонометрических функций с помощью формул:
![]()
![]()
![]()
Пример.Найти интеграл![]() .
.
![]()
![]() .
.
Задачи для самостоятельного решения
94.![]() .
95.
.
95.![]() .
96.
.
96.![]() .
97.
.
97.![]() .
98.
.
98.![]() .
99.
.
99.![]() .
100.
.
100.![]() .
.
101.
![]() .
102.
.
102.![]() .
103.
.
103.![]() .
104.
.
104.![]() .
105.
.
105.![]() .
106.
.
106.![]() .
107.
.
107.![]() .
108.
.
108.![]() .
109.
.
109.![]() .
110.
.
110.![]() .
111.
.
111.![]() .
112.
.
112.![]() .
113.
.
113.![]() .
114.
.
114.![]() .
115.
.
115.![]() .
116.
.
116.![]() .
117.
.
117.![]() .
118.
.
118.![]() .
.
6.10 Интегрирование некоторых иррациональных функций.
Основной приём интегрирования таких функций заключается в рационализации подынтегрального выражения
 .
.
Интеграл берется с помощью подстановки
![]() ,
где
,
где![]() – наименьший общий знаменатель дробей
– наименьший общий знаменатель дробей![]() .
.
Пример.Найти интеграл![]() .
.
Сделаем подстановку
![]() .
.
![]()
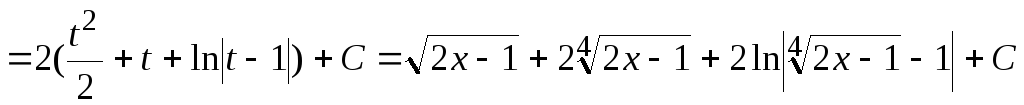 .
.
 .
.
Интеграл рационализуется с помощью тригонометрических подстановок
![]() -
подстановка
-
подстановка![]() ;
;
![]() -
подстановка
-
подстановка![]() ;
;
![]() -
подстановка
-
подстановка![]() .
.
Пример.Найти интеграл![]() .
.
Сделаем подстановку
![]() .
.
![]()
![]()
![]()
![]() .
.
3)
Интегрирование дифференциальных
биномов. Дифференциальным биномом
называется выражение
![]() .
Интегралы
.
Интегралы![]() берутся в элементарных функциях только
в следующих трёх случаях: а)
берутся в элементарных функциях только
в следующих трёх случаях: а)![]() -целое,
-целое,
б)
![]() -
целое. В этом случае делается подстановка
-
целое. В этом случае делается подстановка![]() ,
где
,
где![]() .
.
в)
![]() -
целое. Подстановка
-
целое. Подстановка![]() .
.
Пример.Найти интеграл![]() .
.
![]() .
Здесь
.
Здесь![]() поэтому
имеем второй случай. Подстановка
поэтому
имеем второй случай. Подстановка
![]() ,
,
![]() .
.

Пример.Найти интеграл![]() .
.
 .
.![]() .
Имеем третий случай. Подстановка
.
Имеем третий случай. Подстановка![]() ,
,![]()
![]()
![]() .
.
![]() =
=![]()
![]()
![]()
![]()
4) Интегрирование выражений вида
![]() .
Подстановки Эйлера.
.
Подстановки Эйлера.
а) Если
![]() ,
то применяется первая подстановка
Эйлера:
,
то применяется первая подстановка
Эйлера:![]() ;
;
б) Если
![]() ,
то делается вторая подстановка Эйлера:
,
то делается вторая подстановка Эйлера:![]()
в) Если
![]() имеет различные действительные корни
имеет различные действительные корни![]() и
и![]() ,
то применяется третья подстановка
Эйлера:
,
то применяется третья подстановка
Эйлера:![]()
Пример.Найти интеграл![]() .
.
Т.к.
![]() ,
то применимIподстановку
Эйлера:
,
то применимIподстановку
Эйлера:![]()
![]() ,
,![]()
![]()
![]()
![]()
![]() .
.
Задачи для самостоятельного решения
119.![]() 120.
120.![]() 121.
121.![]() .
.
122.![]() 123.
123.![]() 124.
124.![]() 125.
125.![]() .
.
126.![]() 127.
127.![]() .128.
.128.![]() 129.
129.![]() .
130.
.
130.![]() 131.
131.![]() .
132.
.
132.![]() .
133.
.
133.![]() .
.
134.![]() 135.
135.![]() .
136.
.
136.![]() .
137.
.
137.![]() .
138.
.
138.![]() .
139.
.
139.![]() .
140.
.
140.![]() 141.
141.![]() .
.
