16
,	(3.4)

где – любое число. Причем интеграл слева сходится, если сходятся оба интеграла в правой части.

Пример. Вычислить интеграл

.

►По определению 1

.

Поскольку

то

(3.5)

Таким образом, интеграл расходится при

1

и сходится при 1◄

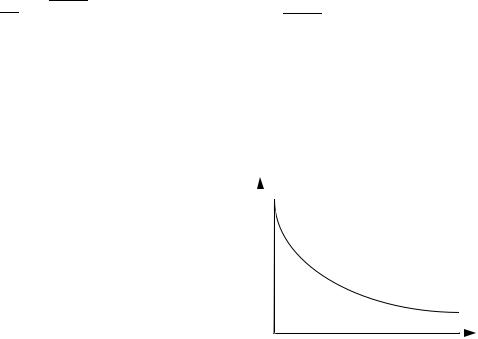
3.1.2. Геометрический смысл несобственных интегралов первого рода

Если функция

неотрицательна на интерва-

y

f (x) 0

ле

:

,

то

y f (x)

f (x) dx S ,

где

- площадь

неограниченной

a

криволинейной трапеции, заключенной между

кривой

, осью абсцисс и прямой

(рис. 3.1).

Аналогично для несобственных интегралов

x

и

.

O

a

Задание.

Сформулировать геометрический

Рис. 3.1

смысл для интегралов

и

.

Для некоторых функций с помощью геометрического смысла интеграла можно определить, является ли интеграл расходящимся.

Пример.	.
►Графиком подынтегральной функции является парабола		. Очевидно, что
площадь фигуры, ограниченной этой параболой и осью абсцисс, равна		. Следовательно,
	◄

3.2.Несобственные интегралы второго рода (от неограниченных функций)

Определение 4. Пусть функция f (x) непрерывна на	интервале [a,b) , а в точке
x b либо не определена, либо терпит разрыв. Точка b	называется особой точкой
функции f (x) . Если существует предел

					17
		b
	lim	f (x) dx ,			(3.6)
	0	a
то его называют несобственным интегралом второго рода от функции				f (x)	на отрезке
	b
[a, b] и обозначают f (x) dx :
	a
	b	def	b
	f (x) dx lim		f (x) dx .		(3.7)
	a	0	a
	Если предел (3.6) конечен, то интеграл называют сходящимся, в противном случае -
расходящимся.
	Определение 5. Пусть функция	непрерывна на интервале		(	– особая
точка функции). Тогда
			.		(3.8)
	Определение 6. Пусть функция	непрерывна на интервале		( и	– особые
точки функции). Тогда
			,		(3.9)
где	. Интеграл в левой части (3.9) сходится, когда сходятся оба интеграла в пра-
вой части.
	Замечание. Если внутри отрезка	есть особые точки функции		, то интеграл

записывается в виде суммы интегралов таким образом, чтобы особые точки были преде-

лами интегрирования. Например, пусть x c - особая точка функции	( a c b ), то-
гда
.	(3.10)

Интеграл слева сходится, если сходится каждый из интегралов в правой части. Это замечание верно и для несобственных интегралов первого рода.

3.3. Применение основной формулы интегрального исчисления (формулы Ньютона-Лейбница)

	Пусть функция	f (x) непрерывна в промежутке [a, ) . Тогда по определению 1 и
по формуле Ньютона-Лейбница:
		B
	f (x) dx lim	f (x) dx lim F (x)		aB lim F (B) F (a) F ( ) F (a) ,
	B	B		B
	a	a
где	F(x) - первообразная функции f (x) ,			F( ) lim F(B) .
				B
	Пусть функция непрерывна на [a,b) ,			x b - особая точки функции. Тогда
		b
		f (x) dx F (b) F (a) ,
		a
где	F(b) lim F(b ) .
	0

Задание. Вывести формулу

							18
1				1		1,
	dx				,
x		1					(3.11)
						1.
0		,

3.4. Свойства несобственных интегралов

Свойства сформулируем для несобственных интегралов первого рода. Для всех остальных несобственных интегралов свойства аналогичны.

1.	Свойство линейности. Пусть функции и непрерывны на промежутке			.
	Тогда
			.
2.	Формула интегрирования по частям. Пусть функции		и	непре-
	рывно дифференцируемы на	. Тогда
		.
3.	Формула замены переменной. Пусть функция		непрерывна на промежутке
	, функция x (t) непрерывно дифференцируема на отрезке [ , ] . Причем
	,	. Пусть, кроме того, функция (t) отображает отре-
	зок [ , ] на промежуток	. Тогда верна формула
	f (x) dx f (t) (t) dt .
	a

Причем оба интеграла либо одновременно сходятся, либо одновременно расходятся.

3.5. Несобственные интегралы от неотрицательных функций Первый признак сравнения. Пусть

1.	b - особая точка функций f (x) ,		g(x) или	b .
2.	f (x), g(x) 0	x [a, b) .
3.		,	.	(3.12)

Тогда:

			b	b
1) если интеграл			g(x) dx	сходится, то сходится и интеграл f (x) dx ;
			a	a
			b	b
2) если интеграл			f (x) dx	расходится, то расходится и интеграл g(x) dx .
			a	a
Второй признак сравнения (предельный). Пусть
1.	b - особая точка функций f (x) , g(x) или b .
2.	f (x) 0,	g(x) 0 x [a, b) .
3.	Существует предел

	lim	f (x)	K .	(3.13)
		g(x)
	x b

Тогда:

19

b

1)

если

интеграл

g(x) dx

сходится

и

, то

сходится

интеграл

a

b

f (x) dx ;

a

b

2)

если

интеграл

g(x) dx

расходится

и

, то расходится

интеграл

a

b

f (x) dx ;

a

b

b

3)

если

0 K ,

то интегралы g(x) dx и

f (x) dx одновременно сходятся или

a

a

одновременно расходятся.

В частности, если

f (x) ~ g(x)

при x b

, то интегралы

b

b

g(x) dx и

f (x) dx одновременно сходятся или одновременно расходятся.

a

a

Аналогичные признаки сравнения можно сформулировать для случая, когда a -

особая точка функций

f (x) ,

g(x)

и когда a .

Часто функция

f (x) сравнивается с функцией

g(x)

1

, так как нам известно, ко-

x

dx

1

dx

гда сходятся интегралы

и

(см. формулы (3.5) и (3.11)).

x

x

1

0

b

Определение. Несобственный

интеграл

f (x) dx называется

абсолютно сходя-

a

b

щимся, если сходится интеграл

f (x)

dx .

a

Поскольку

, то из первого признака сравнения следует, что если несоб-

ственный интеграл сходится абсолютно, то он сходится.

Примеры. Исследовать на сходимость следующие интегралы.

x

3 / 2

1.

dx .

Подынтегральная

функция

непрерывна для любого

1 x

2

0

1

. При x

. Сравним функцию

f (x) с функцией g(x)

.

x1/ 2

1

1

1

1

Рассмотрим

dx

dx

dx . Так как расходится второй интеграл в

x

1/ 2

x

1/ 2

x

1/ 2

0

0

1

				20
			1
правой части, то расходится и интеграл				dx . Следовательно, по следствию к
		x	1/ 2
0

предельному признаку сравнения исследуемый интеграл также расходится.

2.

.

Рассмотрим первый

интеграл в правой части

. Сравним функцию

с

функцией

при

:

. Поскольку

, то по следствию к предельному признаку сравнения интеграл

также расходится. Следовательно, расходится и исследуемый интеграл.

3.

. Поскольку

, то

. Как из-

вестно,

расходится. Тогда расходится и интеграл

. Следовательно, по первому признаку сравнения расходится и исследуемый интеграл◄