Індивідуальні завдання_2011

Міністерство освіти і науки України Дніпропетровський національний університет ім. О. Гончара

Кафедра математичного аналізу і теорії функцій

ІНДИВІДУАЛЬНІ ЗАВДАННЯ З МАТЕМАТИЧНОГО АНАЛІЗУ ЗА ТЕМОЮ

«IНТЕГРАЛЬНЕ ЧИСЛЕННЯ ФУНКЦIЙ ОДНІЄЇ ЗМІННОЇ»

Дніпропетровськ РВВ ДНУ

2012

Наведені основні методи розв’язування задач із інтегрального числення функцій однієї змінної. Для студентів ДНУ, які вивчають курси “Вища математика” і “Математичний аналіз”.

Темплан 2010, поз.

ІНДИВІДУАЛЬНІ ЗАВДАННЯ З МАТЕМАТИЧНОГО АНАЛІЗУ ЗА ТЕМОЮ

«IНТЕГРАЛЬНЕ ЧИСЛЕННЯ ФУНКЦIЙ ОДНІЄЇ ЗМІННОЇ»

Укладачі: канд. фіз.-мат. наук, канд. фіз.-мат. наук, канд. фіз.-мат. наук,

доц. Вакарчук М. Б. доц. Руденко О. О. доц. Чурілова М. С.

Редактор А. Я. Пащенко Техредактор Л. П. Замятіна Коректор

Підписано до друку		.	Формат 60 84/16.	Папір друкарський.
Друк плоский. Ум. друк. арк.			. Ум. фарбовідб.	.
Обл.-вид. арк.		. Тираж 100 пр. Зам.

РВВ ДНУ, просп. Гагаріна, 72, м. Дніпропетровськ, 49010. Друкарня ДНУ, вул. Наукова, 5, м. Дніпропетровськ, 49050.

Передмова

Методи інтегрального числення функцій однієї змінної широко застосовуються у рішенні прикладних задач природничих і технічних наук.

Перша частина видання являє собою опорний конспект, який складається з основних формул і понять. Головну увагу приділено формуванню практичних навиків розв’язування задач. Згідно з цим матеріал систематизовано й поділено на частини таким чином, що можна легко знайти необхідну формулу або визначення. Варто підкреслити, що таке викладення сприяє засвоєнню лекційного матеріалу, але не замінює його.

У другій частині видання вміщені варіанти завдань для індивідуального виконання.

1.Невизначений інтеграл

1.1.Означення, властивості, основні інтеграли та методи інтегрування

Первісна

Первісною функції f на проміжку І називається функція F, така, що

F (x) f (x) x I .

Невизначений інтеграл

f (x)dx F(x) C ,

де F– первісна функції f, С– довільна стала.

Властивості

2. d f (x)dx f (x)dx .

1. f (x)dx f (x) .

4. df (x) f (x) C .

3. f (x)dx f (x) C .

5. kf (x)dx k f (x)dx .

6. (f (x) g(x))dx f (x)dx g(x)dx .

7. Якщо f (x)dx F(x) C , u u(x) – диференційована функція, то

f (u)dx F(u) C .

Основні інтеграли

0 dx C ,

1 dx dx x C ,

xdx

x2

C ,

x

dx

x 1

C,

1,

2

1

dx

dx

1

x ln

x

C ,

x2 x C ,

a x dx

a x

C ,

ex dx ex C ,

ln a

cos xdx sin x C,

sin xdx cos x C ,

tgxdx ln

cos x

C ,

ctgxdx ln

sin x

C ,

3

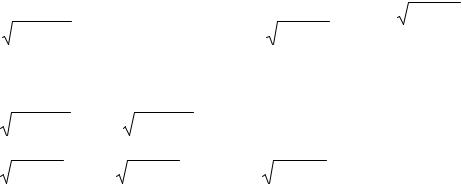
1

dx ctgx C ,

1

dx tgx C ,

sin2 x

cos2 x

1

dx

ln

tg

x

C ,

1

ln

x

C,

dx

tg

sin x

2

cos x

2

4

shxdx chx C ,

chxdx shx C ,

1

dx cthx C ,

1

dx thx C ,

sh2x

ch2x

dx

x

dx

x2

arcsin a C ,

ln

x

C ,

a2 x2

x2

x a

dx

1

x

dx

1

a arctg a C,

ln

C ,

x2 a2

a2

x2 a2

2a

x a

a2 x2 dx x

a2 x2

arcsin x

C ,

2

2

a

x2 dx x

x2

ln

x x2

C .

2

2

Деякі рекурентні формули

2n 3

dx

x

dx

.

(x2 a2 )n

(2n 2)a2 (x2 a2 )n 1

(2n 2)a2

(x2 a2 )n 1

xn ex dx xn ex n xn 1ex dx .

xn sin xdx xn cos x n xn 1 cos xdx .

xn cos xdx xn sin x n xn 1 sin xdx .

Деякі інтеграли, що не є елементарними функціями

ex 2 dx ,

e x 2 dx ,

sin x2dx ,

cos x2dx ,

sin x

dx,

n N,

cos x

dx,

n N

ex

dx, n N,

xn

xn

xn

x

dx ,

x

dx ,

tgxdx ,

ctgxdx ,

xtgxdx ,

xctgxdx ,

sin x

cos x

x

x

arcsin x

dx ,

arccos x

dx ,

arctgxdx ,

arcctgxdx ,

x

x

x

x

dx

,

xdx

,

x2dx

,

dx

,

ln x

ln x

ln x

x2 ln x

ex ln xdx ,

lnsin xdx ,

ln cos xdx ,

lntgxdx .

Заміна змінної у невизначеному інтегралі

1.f (u(x))u (x)dx f (u)du F(u) C F(u(x)) C .

2.Якщо x (t), (t) 0 , F– первісна для (g ) , то

g(x)dx g( (t)) (t)dt F(t) C F( 1(x)) C .

4

Інтегрування частинами

udv uv vdu .

Вінтегралах xn eax dx , xn sin bxdx , xn cosbxdx за u позначають xm , а за dv – решту виразу. В інтегралах xn lnm dx , xn arcsin xdx , xn arccosxdx , xn arctgxdx

за dv позначають dx, а за u – решту виразу. В інтегралах eax sin bxdx ,eax cos bxdx формулу інтегрування частинами застосовують двічі.

1.2. Інтегрування раціональних функцій

Інтегрування елементарних раціональних функцій

1.

A

A ln

x

C .

x

2.

A

A

C,

k 1.

(x )k

(1

k)(x )k 1

3.

Mx N

dx,

p2 4q 0 , заміною x p t зводиться до лінійної комбінації

x2 px q

2

інтегралів

tdt

1 ln(t2

a 2 ) C та

dt

1 arctg

t

C .

t

2 a2

t2 a2

a

2

a

4.

Mx N

dx,

p2

4q 0,

k 1,

заміною x p

t

зводиться до лінійної

(x2 px q)k

2

комбінації

інтегралів

tdt

1

C та

dt

.

(t2 a2 )k

2(1 k)(t2

a2 )k 1

(t2 a2 )k

Останній обчислюється за рекурентною формулою.

Розклад правильної дробово-раціональної функції на елементарні дроби

Якщо P(x), Q(x) – многочлени, степінь P(x) менше ніж Q(x) і Q(x) (x 1)k1

(x 2 )k 2 ... x2 p1x q1 l1 x2 p2x q2 l2 ..., де pi2 4qi 0, то

		P(x)					A	1						A	2				...		Ak	1	...+
		Q(x)			(x 1)								(x )2							(x )k1
																1						1
	M		x N							M		2	x	N		2					Ml x Nl			1
	1			1															...			1				...
	x2 p x			q					(x	2 p x q							)2				(x2 p x q
						1																			)l1
			1										1			1						1		1

Після множення на Q(x) невідомі коефіцієнти знаходять із умові тотожної рівності двох многочленів.

Інтегрування раціональної функції у загальному випадку

Будь-яку раціональну функцію можна подати у вигляді S(x) QP((xx)) , де S, P, Q –

многочлени і степінь P менше ніж Q. Після розкладу P(x) / Q(x) інтегрування раціональної функції зводиться до інтегрування елементарних дробів.

5

1.3. Метод раціоналізації

Нехай R(u,v,…,s) – раціональна функція від u,v,…,s.

Інтегрування ірраціональностей від дробово-лінійної функції

n

ax

b

n

ax b

R

раціоналізує підстановка t

.

x,

cx d

dx , (ad bc)

cx

d

m1

m2

mk

R

ax b n1

ax b n2

ax b nk

раціоналізує підстановка

x,

,

,...,

dx , (ad bc)

cx d

cx d

cx d

tn

ax b

, де n – найменше спільне кратне чисел n1 ,n2 ,...nk .

cx d

m1

m2

mk

R

n1

, x

n2

,..., x

nk

підстановка

t

n

x ,

де n – найменше

x, x

dx раціоналізує

спільне кратне чисел n1 ,n2 ,...nk .

Інтегрування біноміальних диференціалів

xm (a bxn )p dx, m,n,p Q, ab 0

раціоналізується лише у трьох випадках:

1. р Z; підстановка x tk , де k– спільний знаменник m и n;

2. m 1 Z; підстановка a bxn tk , де k–знаменник p; n

3. m 1 p Z; підстановка ax n b tk , де k–знаменник p. n

Інтегрування раціонально-тригонометричних функцій

R(sin x,cos x)dx завжди раціоналізує універсальна підстановка tg(x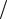2) t

		2t		1 t2		2dt
	sin x		, cos x		, dx		.
		1 t2		1 t2		1 t2

Спеціальні підстановки

1.Якщо R( sin x,cos x) R(sin x,cos x) , то раціоналізує підстановка cos x t .

2.Якщо R(sin x, cos x) R(sin x,cos x) , то раціоналізує підстановка sin x t .

3.Якщо R( sin x, cos x) R(sin x,cos x) , то раціоналізує підстановка tgx t .

Обчислення інтегралів виду R( x , ax2 bx c )dx

Підстановки Ейлера:

1.a 0 ; раціоналізують підстановки ax2 bx c ax t;

2.c 0 ; раціоналізують підстановки ax2 bx c tx c ;

3.b2 4ac 0, ax2 bx c t(x x1 )(x x2 ) ; раціоналізують підстановки

ax2 bx c t(x xi ) , де i 1 або i 2 .

В окремих випадках доцільні наступні тригонометричні підстановки:

6

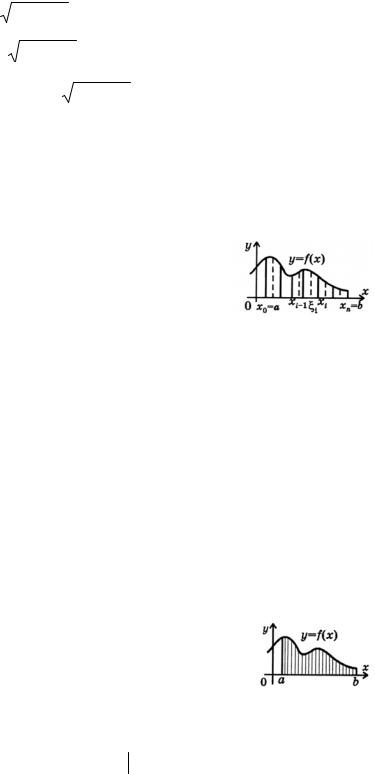
	R(x,	a2 x2 )dx,		x a sin t			або x a cos t ,
	R(x,	x2 a 2 )dx,		x		a	або x	a	,
					cos t			sin t
		R(x,	x2 a2 )dx,			x a tgt .

2.Визначений інтеграл

2.1.Означення, властивості, методи інтегрування

Визначений інтеграл

b

n

f (x)dx lim

f ( i ) xi

, де

a

max

xi 0 i 1

xi 1 i xi ,

xi xi xi 1

(рис. 1).

Рис. 1

Властивості

b

b

b

b

b

a

1.

Cf (x)dx C f (x)dx .

2. (f (x) g(x))dx f (x)dx g(x)dx

3.

f (x)dx 0.

a

a

a

a

a

a

b

a

b

c

b

b

4.

f (x)dx f (x)dx .

5.

f (x)dx f (x)dx f (x)dx .

6

dx b a .

a

b

a

a

c

a

b

b

b

7. f (x) 0 f (x)dx

0, a b .

8. f (x) g(x) f (x)dx g(x)dx, a b .

a

a

a

b

b

b

9.

f (x)dx

f (x)

dx, a b .

10.

m(b a) f (x)dx M(b a) ,

де m min f (x) ,

a

x a,b

a

a

M max f (x) .

11.

b

f (x)dx f ( )(b a), a,b (теорема про середнє значення).

x a,b

a

Геометричний зміст

b

Якщо f (x) 0 S f (x)dx – площа

a

криволінійної трапеції (рис. 2).

Рис. 2

Формула Ньютона-Лейбніца

b f (x)dx F(x) ab F(b) F(a) .

a

Заміна змінної у визначеному інтегралі

b			( ) a, ( ) b .
f (x)dx f ( (t)) (t)dt ;
a

Інтегрування частинами

b			b	b
u(x)v (x)dx u(x)v(x)			a	v(x)u (x)dx .
a				a

7

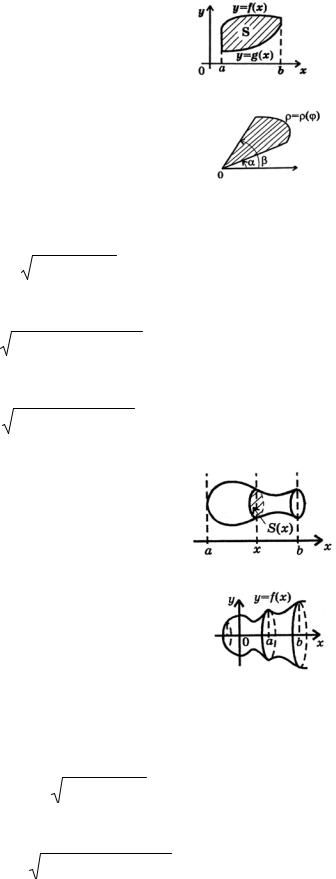
2.2. Застосування визначеного інтеграла у геометрії

Обчислення площі

Площа у прямокутних координатах (рис. 3)

b
S (f (x) g(x))dx
a
Площа криволінійного сектора у полярних координа-		Рис. 3
тах. ( ) –рівняння кривої, (рис. 4).
S 1
	2 ( )d .
2

Рис. 4

Обчислення довжини плоскої кривої

Довжина кривої у прямокутних координатах. y=f(x) – рівняння кривої, a x b ,

	b				2
l						dx .
		1 (f (x))
	a
Довжина кривої, заданої параметрично: x=x(t), y=y(t); t 0 t t1 ,
t1			2				2	dt .
l	(x (t))			(y (t))
t0

Довжина кривої у полярних координатах. ( ) – рівняння кривої,

2

2

l

d .

( )

(

( ))

Обчислення об’єму тіла

Об’єм тіла з відомою площею

перерізу (рис. 5).

b

V S(x)dx .

a

Об’єм тіла обертання навколо

Рис. 5

осі Ох (рис. 6).

b

Vx f 2 (x)dx .

a

Об’єм тіла обертання навколо осі Оy

b

Vy 2 xf (x)dx .

Рис. 6

a

Обчислення площі поверхні обертання

Одержаної обертанням кривої y=f(x) a x b навколо осі Ох

b

2

dx

S 2 f (x) 1 (f (x))

a

t t1 , навколо осі Ох

Одержаної обертанням кривої x=x(t), y=y(t); t 0

t1

2

2

S 2 y(t)

dt

(x (t))

(y (t))

t0

8

Завдання для самостійної роботи

1. Обчислити інтеграл за допомогою заміни змінної.

1.а)						dx			;
			1 x2 arcsin x
2.а)			dx					;
		x sin		2	ln x
3.а)		earctgx			dx ;
	1		x	2
4.а)		3x 1 dx				;
	1		9	x 1

5.а) x arccos3 x2 dx ; 1 x4

6.а) 5 2 3cos x sin xdx ;

7.а) sincostgx2 x dx ;

8.а) x6dx ; x14 49

9.а) x sin 2x2dx ;

10.а) 4ctgxdxsin 2 x ;

б) 2x 3 10 dx ;

б) 3 1 3xdx ;
б)				dx				;
				5
	5x 2					2
б) ex3 x2dx ;
б)				dx	;
		2		2
				3x
б)				dx			;
				2 5x
б)		5		1 2x		x2			dx ;
				1 x

б) e x e 2x dx ;

б)			dx		;
		2	3x	2
б)			dx			;
		2 3x2

в)

xe x3 dx .

ex dx

в)

.

2

e

x

в)

ln2 x

dx .

x

в)

sin5 x cos xdx .

в)

dx

.

e

x

x

e

в)

dx

.

x ln x ln ln x

в)

dx

.

1 e2x

в)

arctgx2 dx .

1 x

в)

dx

.

arcsin2 x

1 x2

ln x

1 x2

в)

dx .

1 x

2

9

11. а)			dx				;
		sh2 x3			thx
12.а)			dx			;
	1		x		x
13.а)	e		x dx	;
			x

					1 x2
		5	ln x
14.а)
									dx ;
			1	x2
15.а) sh arctg2							x 1 dx ;
			x 2x 2
16.а) shxdx3					;
		ch x
17.а)		arctg2x 3									;
										dx
			1 x			2

18.а) ln2 x			1 x2 dx	;
		1 x2
19.а)	x	3dx	;
	1	x8

20.а) arcsin x 1 dx ; 2x x2

21.а) 3 arctg x 2 dx ; x2 4x 5

б) 3xdx2 2 ;

б) sin 5x sin 5 dx ;

б)

dx

;

sin

2

2x

4

б)

xdx

;

3

2x

2

б)

dx

;

1

cos x

б)

xdx

;

1 x2

б)

xdx

;

1

x2

2

б)

dx

;

1 cos x

б) sin 1

dx2 ;

x

x

б) 3 1 x3 x2dx ;

б) xx83dx2 ;

в) x5x4 1 4 dx .

	в)		ln xdx	.
		x	1 ln x

в) x 1 x 10 dx .

в) tgxdx .

в)

dx

.

1 ex

в)

sin x

dx .

cos3 x

в)

dx

.

sin

2

x4

ctgx

в)

dx

.

e

x

2 ex

в)

arctg x

dx

.

x

1 x

в)

1

ln

1 x dx .

1

x

2

1 x

в) ctgxdx .

10