
- •Практикум
- •Занятие 7.
- •Задачи для самостоятельного решения
- •Занятие №9.
- •Правило Лопиталя.
- •Производная функции, заданной параметрически.
- •Примеры
- •Как определять интервалы выпуклости (вогнутости) и точки перегиба графика функции:
- •Задачи для самостоятельного решения
- •Перечень вариантов домашней контрольной работы по теме «Исследование функций и построение их графиков»
- •Список литературы
- •Скворцова Мария Ивановна Мудракова Ольга Александровна Кротов Герман Сергеевич
Задачи для самостоятельного решения
Написать уравнения касательной и нормали к кривой в заданной точке
 :
:
а)
![]() ;
;
б)
![]() ;
;
в)
![]() .
.
В какой точке касательная к параболе

а)
параллельна прямой
![]() ?
?
б)
перпендикулярна прямой
![]() ?
?
Найти дифференциал
 следующих функций :
следующих функций :
а)
![]() ;б)
;б)
![]() ;в)
;в)
![]() .
.
Вычислить приближённо:
а)
![]() ;б)
;б)
![]() .
.
Ответы
а)
 ;
б)
;
б) ;
в)
;
в) .
.а)
 ;
б)
;
б) .
.
4) а) 2,25; б) 1.
Занятие №9.
Правило Лопиталя для вычисления пределов. Производная функции, заданной параметрически.
Правило Лопиталя.
1)
Пусть надо найти
![]() ,
где
,
где![]() (или
(или![]() ),
т.е. имеет место неопределённость вида
),
т.е. имеет место неопределённость вида![]() или
или![]() .Тогда:
.Тогда:
![]() .
.
(Предполагается,
что существуют производные
![]() в окрестности точки
в окрестности точки![]() ,
а также существует предел, стоящий
справа).
,
а также существует предел, стоящий
справа).
2)
Пусть надо найти
![]() ,
где
,
где![]() ,
,![]() ,
т.е. имеется неопределённость вида
,
т.е. имеется неопределённость вида![]() .
Тогда следует сделать преобразование:
.
Тогда следует сделать преобразование: ,
получив неопределённость вида
,
получив неопределённость вида![]() ,
и воспользоваться указаниями в п.1).
,
и воспользоваться указаниями в п.1).
3)
Пусть надо найти
![]() ,
где
,
где![]() ,
,![]() ,
т.е. имеется неопределённость вида
,
т.е. имеется неопределённость вида![]() .
Тогда сделать подходящее преобразование
выражения
.
Тогда сделать подходящее преобразование
выражения![]() и прийти к случаю 1) или 2).
и прийти к случаю 1) или 2).
4)
Пусть надо найти
![]() ,
где имеется неопределённость вида
,
где имеется неопределённость вида![]() .
Пользуясь свойствами логарифма,
преобразуем данный предел:
.
Пользуясь свойствами логарифма,
преобразуем данный предел:
![]()
Таким образом, вычисление исходного предела сводится к вычислению предела
![]() .
.
Замечание.
Возможна ситуация, когда существует
![]() ,
но не существует
,
но не существует![]() .
Тогда правило Лопиталя не применимо.
.
Тогда правило Лопиталя не применимо.
Производная функции, заданной параметрически.
Пусть
функция
![]() задана параметрически:
задана параметрически:

Тогда
её производная
![]() находится по следующей формуле:
находится по следующей формуле:
![]() .
.
Примеры
Найти пределы, используя правило Лопиталя:
 ;
; ;
;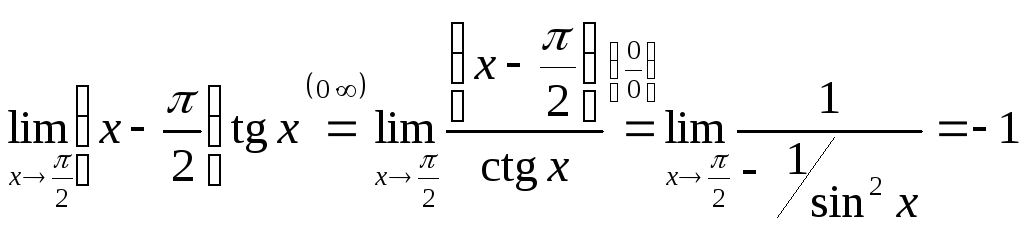 ;
;
 ;
; ;
; ;
; ;
;Найти
 для функции
для функции ,
заданной параметрически:
,
заданной параметрически:
а)
 ;
;
 ;
;
б)
 ;
;
 .
.
Задачи для самостоятельного решения
Найти пределы:
1)
 ;2)
;2)
![]() ;3)
;3)
![]() ;4)
;4)
![]() ;5)
;5)
![]() ;6)
;6)
![]() ;7)
;7)
![]() ;8)
;8)
![]() ;9)
;9)
![]() ;10)
;10)
![]() ;11)
;11)
![]() ;12)
;12)
![]() ;13)
;13)
![]() ;14)
;14)
![]() ;15)
;15)
![]() .
.
16)
Найти
![]() :
а)
:
а) ,
б)
,
б) ,
в)
,
в) .
.
Ответы
1)
![]() ;
2) –2; 3)
;
2) –2; 3)![]() ;
4) 1; 5)
;
4) 1; 5)![]() ;
6)
;
6)![]() ;
7) 0; 8) 1; 9) 0; 10) 0; 11)
;
7) 0; 8) 1; 9) 0; 10) 0; 11)![]() ;
12)
;
12)![]() ;
13) 1; 14)
;
13) 1; 14)![]() ;
15) 1; 16) а)
;
15) 1; 16) а)![]() ;
б)
;
б)![]() ;
в)
;
в)![]() .
.
Занятие №10
Контрольная работа №2 по теме
«Производная функции одной переменной».
Вариант-образец
Написать уравнения касательной и нормали к параболе
 в точке с абсциссой
в точке с абсциссой .
.
Уравнения касательной и нормали в общем виде:
![]() ,
,
![]() .
.
Здесь
![]() ;
;![]() .
Поэтому уравнения касательной и нормали
имеют следующий вид:
.
Поэтому уравнения касательной и нормали
имеют следующий вид:
![]() или
или
![]() ;
;
![]() или
или
![]() .
.
Найти производную
 для заданной функции
для заданной функции :
:
а)
![]() ;
;
 ;
;
б)
 ;
;

 .
.
в)
![]() ;
;
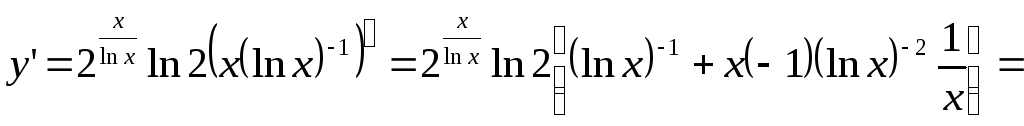
 .
.
г)
![]() ;
;
Используем логарифмическое дифференцирование:
 ;
;
![]() ,
,
![]() .
.
д)

Производная функции, заданной параметрически, вычисляется по формуле:
 .
.
Так
как здесь
![]() ,
то
,
то![]() .
.
Занятие №11
Исследование функций:
нахождение интервалов возрастания (убывания) функции, экстремумов, интервалов выпуклости (вогнутости), точек перегиба, асимптот графика функции
Определение.
Точка
![]() называетсяточкой
максимума
(минимума)
функции
называетсяточкой
максимума
(минимума)
функции
![]() ,
если
,
если![]() окрестность точки
окрестность точки![]() вида
вида![]() ,
такая что
,
такая что![]()
![]() для
для![]() из этой окрестности. Точки максимума и
минимума называютсяточками
экстремума функции
из этой окрестности. Точки максимума и
минимума называютсяточками
экстремума функции
![]() .
.
Определение.
Функция
![]() называетсявозрастающей
(убывающей)
на числовом промежутке
называетсявозрастающей
(убывающей)
на числовом промежутке
![]() ,
если для
,
если для![]() таких, что
таких, что![]() :
:
![]()
![]() .
.
Определение.
Точка
![]() ,
в которой функция
,
в которой функция![]() определена, но либо
определена, но либо![]() ,
либо
,
либо![]() ,
либо
,
либо![]() не существует, называетсякритической
точкой 1-го рода.
не существует, называетсякритической
точкой 1-го рода.
Как определять интервалы возрастания (убывания) функции и точки экстремума:
1)
Найти
![]() ;2)
определить критические точки 1-го рода
для
;2)
определить критические точки 1-го рода
для
![]() ;3)
нанести эти точки, а также точки разрыва
функции, на числовую ось; 4)
определить знак
;3)
нанести эти точки, а также точки разрыва
функции, на числовую ось; 4)
определить знак
![]() в каждом из интервалов, на которые эти
точки разбивают числовую ось.
в каждом из интервалов, на которые эти
точки разбивают числовую ось.
Если
![]()
![]() на рассматриваемом интервале, то
на рассматриваемом интервале, то![]() возрастает (убывает) на этом интервале.
Если при переходе аргумента
возрастает (убывает) на этом интервале.
Если при переходе аргумента![]() через критическую точку
через критическую точку![]() слева направо
слева направо![]() меняет знак с «+» на «—» (с «+» на «—»),
то
меняет знак с «+» на «—» (с «+» на «—»),
то![]() — точка максимума (минимума). Если смены
знака
— точка максимума (минимума). Если смены
знака![]() не происходит, то в точке
не происходит, то в точке![]() нет экстремума. Заметим, что все
вышеуказанные данные можно поместить
в таблицу, как это сделано в приводимых
далее примерах.
нет экстремума. Заметим, что все
вышеуказанные данные можно поместить
в таблицу, как это сделано в приводимых
далее примерах.

