Тема 5. Выборочное наблюдение

Задача 5.1.

Имеется информация о выпуске продукции (работ, услуг), полученной на основе 10% выборочного наблюдения по предприятиям области:

Группы предприятий	Число
по объему продукции,	предприятий
тыс. руб.	(f)
1	2
До 100	28
100-200	52
200-300	164
300-400	108
400-500	36
500 и >	12
	400
Итого

Определить: 1) по предприятиям, включенным в выборку: а) средний размер произведенной продукции на одно предприятие; б) дисперсию объема производства; в) долю предприятий с объемом производства продукции более 400 тыс. руб.; 2) в целом по области с вероятностью 0,954 пределы, в которых можно ожидать: а) средний объем производства продукции на одно предприятие; б) долю предприятий с объемом производства продукции более 400 тыс. руб.; 3) общий объем выпуска продукции по области.

Решение.

По исходным данным составим таблицу 1

			Таблица 1
	Группы
	предприятий по	Среднее в	Число
	объему		предприятий
		группе (xi)
	продукции, тыс.		(ni)
	руб.
	0-100	50	28
	100-200	150	52
	200-300	250	164
	300-400	350	108
	400-500	450	36
	500-600	550	12
	Итого		400

106

1. Средний размер произведенной продукции на одно предприятие равен

∑xi ni

50 28 +... +550

12

110800

x = ∑ni

=

=

= 277,0 тыс. руб.

28 +... +12

400

Дисперсия объема производства равна

σ2 = ∑

(xi − x)2 ni

=

(50 − 277)2 28 +... + (550 − 277)

2 12

=

4948400

=12371,0 .

∑ni

28 +... +12

400

Доля предприятий с объемом производства продукции более 400 тыс. руб. составляет

∑ni

36 +12

48

w =

xi >400

=

=

= 0,12 .

∑ni

400

400

2. Предельная ошибка признака равна

х = t

σ2

−

n

= 2

12371

(1

−0,1)

= 2 27,835 =10,552

тыс. руб.,

n

1

400

N

t = 2, при р = 0,954.

х − х ≤ μx ≤ х + х,

277 −10,552 ≤ μx ≤ 277 +10,552 , 266,448 ≤ μx ≤ 287,552 ,

т.е. с вероятностью 0,954 можно утверждать, что средний объем производства продукции на одно предприятие генеральной совокупности (по всем предприятиям области) не ниже

266,448 тыс.руб. и не выше 287,552 тыс. руб.
2. Предельная ошибка доли равна
w = t	w (1 − w)		−	n	0,12 (1 −0,12)	(1	−0,1)	= 2 0,0002376 = 0,0308 ,
	n	1		= 2	400
				N
w − w ≤ p ≤ w +		w ,

0,12 − 0,0308 ≤ p ≤ 0,12 + 0,0308 ,

0,0892 ≤ p ≤ 0,1508 , или 8,92% ≤ p ≤15,08% ,

т.е. с вероятностью 0,954 можно утверждать, что доля предприятий с объемом производства продукции более 400 тыс. руб. в генеральной совокупности (по всем предприятиям области) будет находиться в границах не ниже 8,92% и не выше 15,08%.

Общий объем выпуска продукции по области равен

	V =	x n	=	277 400	=1108000	тыс. руб.
		n		0,1

N

107

Задача 5.2.

По результатам контрольной проверки налоговыми службами 400 бизнес-структур, у 140 из них в налоговых декларациях не полностью указаны доходы, подлежащие налогообложению. Определите в генеральной совокупности (по всему району) долю бизнесструктур, скрывших часть доходов от уплаты налогов, с вероятностью 0,954.

Решение.

Доля бизнес-структур, скрывших часть доходов от уплаты налогов, в выборочной совокупности составляет

w =	m	=	140	= 0,35 .
			400
	n
Предельная ошибка доли равна
w = t			w (1 − w) = 2		0,35 (1 −0,35)	= 2 0,00056875 = 0,048 ,
				n	400

t = 2, при р = 0,954. w − w ≤ p ≤ w + w ,

0,35 − 0,048 ≤ p ≤ 0,35 + 0,048 ,

0,302 ≤ p ≤ 0,398 , или 30,2% ≤ p ≤ 39,8% ,

т.е. с вероятностью 0,954 можно утверждать, что доля бизнес-структур, скрывших часть доходов от уплаты налогов в генеральной совокупности (по всему району) будет находиться в границах не ниже 8,92% и не выше 15,08%.

Задача 5.3.

В целях изучения стажа рабочих одного из цехов завода проведена 10%-ная механическая выборка, в результате которой получено следующее распределение рабочих по стажу работы:

Стаж рабочих, лет		Число рабочих, чел
До	5	5
От 5 до 10		10
От 10 до 15		35
От 15 до 20		25
От 20 до 25		15
Свыше 25		10
Итого		100

На основании этих данных вычислите: 1. Средний стаж рабочих цеха.

108

2.Средний квадрат отклонений (дисперсию) и среднее квадратическое отклонение.

3.Коэффициент вариации.

4.С вероятностью 0,997 предельную ошибку выборочной средней и возможные границы, в которых ожидается средний стаж рабочих цеха.

5.С вероятностью 0,997 предельную ошибку выборочной доли и границы удельного веса числа рабочих со стажем работы от 10 до 20 лет.

Сделайте выводы.

Решение.

Запишем исходные данные в виде таблицы 1.

										Таблица 1
	Стаж рабочих, лет						В среднем в группе xi, лет		Число рабочих ni, чел
		0	- 5				2,5			5
		5 - 10					7,5			10
		10	- 15				12,5			35
		15	- 20				17,5			25
		20	- 25				22,5			15
		25	- 30				27,5			10
		Итого								100
Средний стаж рабочих цеха определим по формуле средней арифметической
взвешенной
x =		∑xi ni	=	2,5 5 +7,5 10 +12,5 35 +17,5 25 + 22,5 15 + 27,5 10						=	1575		=15,75 лет.
		∑ni				5 +10 +35 + 25 +15 +10						100
Дисперсия равна
σ2x		= ∑(xi	− x)2 ni =		4068,75			= 40,69 .
		∑ni				100

Среднее квадратическое отклонение равно

σx = σ2x = 40,69 = 6,38 лет.

Коэффициент вариации равен

v = σxx = 156,,3875 = 0,405 , или 40,5%.

Определим с вероятностью 0,997 предельную ошибку выборочной средней и возможные границы, в которых ожидается средний стаж рабочих цеха.

По условию задачи имеем 10% бесповторную, собственно-случайную, механическую выборку. Т.к. обследовано 10% рабочих, то

109

Nn = 0,1,

где n = 100 – объем выборочной совокупности, N – объем генеральной совокупности.

При доверительной вероятности p = 0,997 коэффициент доверия t = 3. Тогда предельная ошибка выборки равна

		= t	σ2x		−	n	= 3	40,69	(1	−0,1)	= 3 0,3662 =1,815 .
			n	1				100
x
						N

Определим возможные границы, в которых находится средний размер прибыли в генеральной совокупности:

x − x ≤ μx ≤ x + x .

Подставив имеющиеся данные, получим

15,75 −1,815 ≤ μx ≤15,75 +1,815 , или 13,935 ≤ μx ≤17,565 .

Определим с вероятностью 0,997 предельную ошибку выборочной доли и границы удельного веса числа рабочих со стажем работы от 10 до 20 лет.

Выборочная доля числа рабочих со стажем работы от 10 до 20 лет составляет

W = 60/100 = 0,6 или 60%.

Отсюда дисперсия доли равна:

σW2

=W (1 −W ) = 0,6 0,4 = 0,24 .

Тогда предельная ошибка выборки равна:

= t

σW2

n

0,24

n

1 −

= 3

100

(1

−0,1)

= 2

0,004838

= 0,1391.

W

N

Определим возможные границы удельного веса числа рабочих со стажем работы от 10 до 20 лет:

W − W ≤ Ω ≤W + W .

Подставив имеющиеся данные, получим

0,461 ≤ Ω ≤ 0,739 , или 46,1% ≤ Ω ≤ 73,9% .

Задача 5.4.

Для определения средней величины заработной платы работников малых предприятий необходимо провести выборочное обследование методом случайного повторного отбора. Какое количество работников нужно отобрать, чтобы ошибка выборки с вероятностью 0,954 не превышала 2 тыс. руб. при среднем квадратическом отклонении 10 тыс. руб.

Решение.

110

Предельная ошибка признака для случайного повторного отбора равна

	х = t	σ2	,
		n

отсюда

( х)2 = t 2 σ2 . n

следовательно, n = tσx .

Т.к. по условию σ =10 и t = 2, при р = 0,954, то имеем n = tσx = 2 210 =10 чел.

Таким образом, необходимо отобрать не менее 10 работников, чтобы ошибка выборки с вероятностью 0,954 не превышала 2 тыс. руб.

Задача 5.5.

Среди выборочно обследованных 13000 семей по уровню дохода-(выборка бесповторная, 2%) малообеспеченных оказалось – 3900 семей. Определите с вероятностью 0,997 долю малообеспеченных семей во всем регионе.

Решение.

Т.к. обследовано 2% семей, то

Nn = 0,02 ,

где n – объем выборочной совокупности, N – объем генеральной совокупности. При доверительной вероятности p = 0,997 коэффициент доверия t = 3. Выборочная доля малообеспеченных семей составляет

W = 3900/13000 = 0,3 или 30%.

Отсюда дисперсия доли равна:

σW2 =W (1 −W ) = 0,3 0,7 = 0,21.

Тогда предельная ошибка выборки равна:

		= t	σW2		−	n	= 3	0,21	(1	−0,02)	= 0,012 .
			n	1				13000
	W
						N

Определим возможные пределы доля малообеспеченных семей:

W − W ≤W ≤W + W .

111

Подставив имеющиеся данные, получим

0,298 ≤W ≤ 0,312 , или 29,8% ≤W ≤ 31,2% .

Задача 5.6.

Для определения среднего возраста студентов вуза с числом студентов 1250 был зафиксирован возраст 87 студентов (см. табл.)

Возраст	17	18	19	20	21	22
Число студентов	23	25	5	8	3	23

Определите:

1)средний возраст студентов выборки;

2)среднеквадратическое отклонение возраста по выборке;

3)99% доверительный интервал для среднего возраста студентов вуза.

Решение.

Средний возраст студентов выборки равен

n

x

∑xi ni

17 23 +... + 22

23

1665

=

i=1

=

=

=19,14 .

n

23 +... + 23

87

∑ni

i=1

Среднеквадратическое отклонение возраста по выборке равно

n

∑

(xi

− x)2 ni

(17

−19,14)

2

23 +... + (22

−19,14)

2

23

342,345

=1,984 .

σ

x

=

i=1

=

=

n

23 +... + 23

87

∑ni

i=1

По условию задачи

n

=

87

= 0,0696 ,

N

1250

где n – объем выборочной совокупности, N – объем генеральной совокупности.

При доверительной вероятности p = 0,99 коэффициент доверия t = 2,58. Тогда

предельная ошибка выборки равна:
			σ2x			n		1,984	2
		= t	n	1	−		= 2,58	87	(1 −0,0696) = 0,529 .
	x
						N

Определим возможные границы, в которых находится средний возраст в генеральной совокупности:

112

x − x ≤ μx ≤ x + x .

Подставив имеющиеся данные, получим

19,14 −0,529 ≤ μx ≤19,14 +0,529 , или 18,61 ≤ μx ≤19,67 .

Задача 5.7.

В городе проводится обследование семей с целью выявления доли расходов семейных бюджетов на оплату жилья. Предыдущее аналогичное обследование дало результат в 21,6%. Сколько нужно обследовать семей, чтобы с вероятностью 0,99 и точностью не менее 0,5% определить эту долю?

Решение.
Искомое число семей равно
n =	t 2	σ	2	=	2,582 0,216 (1 −0,216)		= 45089 .
		2			0,005	2
		~
		x

Задача 5.8.

Для оценки стоимости основных средств региона проведен 5%-ный механический отбор, в результате чего установлено:

	Группы предприятий по стоимости	Число предприятий
	основных средств, млн. р.
	До 10	131
	10 – 20	227
	20 – 30	294
	30 – 40	146
	40 – 50	128
	50 и выше	74
	Итого	1000

Определить:

1)с вероятностью 0,954 пределы, в которых можно ожидать среднюю стоимость основных средств на одно предприятие и долю предприятий со стоимостью выше 50 млн. р. В целом по региону;

2)ожидаемую сумму налога на имущество (2%) со стоимости основных средств по обследованной группе предприятий и по региону в целом.

Сделать выводы.

113

Решение.

Преобразуем исходную таблицу, сопоставив интервалам стоимости основных средств их средние значения. В результате получим следующую таблицу

	Группы предприятий по стоимости	Число предприятий (ni)
	основных средств, млн. р. (xi)
	5	131
	15	227
	25	294
	35	146
	45	128
	55	74
	Итого	1000

1. Определим вначале среднюю стоимость основных средств на одно предприятие по формуле средней арифметической взвешенной

	L
x =	∑xi ni	=	5 131 +15 227 +K+55 74	=	26350	= 26,35 млн. р.
	i=1
	L
			131 + 227 +K+ 74		1000
	∑ni
	i=1

По формуле моментов дисперсия стоимость основных средств на одно предприятие равна

L

sx2 =

−(x)2

∑xi2 ni

−(x)2

=

5

2

131 +15

2

227 +K+55

2

74

− 26,352 = .

x2

=

i=1

n

1000

= 900 −694,322

= 205,678.

Отсюда среднее квадратическое отклонение равно

sx = D[x] =

205,678 =14,341.

По условию задачи имеем бесповторную, собственно-случайную, механическую выборку.

Т.к. обследовано 5% банков,

то

n

= 0,05 , где n –

объем выборочной совокупности, N –

N

объем генеральной совокупности.

При доверительной вероятности p = 0,954 коэффициент доверия t = 2. Тогда предельная

ошибка выборки равна:

= t

sx2

n

205,678

0,195 = 0,884 .

1

−

= 2

(1

−0,05)

= 2

x

n

N

1000

Определим возможные границы, в которых находится средняя стоимость основных средств на одно предприятие:

x − x ≤ μx ≤ x + x .

114

Подставив имеющиеся данные, получим

26,35 −0,884 ≤ μx ≤ 26,35 +0,884 , или 25,466 ≤ μx ≤ 27,234 .

Выборочная доля предприятий со средней стоимостью основных средств выше 50 млн. р. составляет

W = 74/1000 = 0,074 или 7,4%.

Отсюда дисперсия доли равна:

σW2 =W (1 −W ) = 0,074 0,926 = 0,0685 .

Тогда предельная ошибка выборки равна:

		= t	σW2		−	n	= 2	0,0685	(1	−0,05)	= 0,0051 .
			n	1				1000
	W
						N

Возможные пределы среднего значения доли предприятий со средней стоимостью основных средств выше 50 млн. р. составляют

W − W ≤W ≤W + W .

Подставив имеющиеся данные, получим

0,0689 ≤W ≤ 0,0791 , или 6,89% ≤W ≤ 7,91% .

Ожидаемая сумма налога на имущество (2%) со стоимости основных средств по обследованной группе предприятий составит

R = 0,02nx = 0,02 1000 26,35 = 500 26,35 = 527 млн. р.

Ожидаемая сумма налога на имущество (2%) со стоимости основных средств по региону в целом составит

25,466 500 20 ≤ Rx ≤ 27,234 500 20 , или 25465,9 ≤ Rx ≤ 27234,1.

Задача 5.9.

На оптовую базу поступила партия товара. После тщательного осмотра каждой единицы товара определялось и фиксировалось его качество. К какому виду наблюдения (и по каким признакам) можно отнести это обследование товара.

Решение.

Статистическое наблюдение – это планомерный научно обоснованный сбор данных или сведений о явлениях и процессах общественной жизни.

По организационной форме статистического наблюдения – это специально организованное наблюдение.

По виду статистического наблюдения – это:

115

-единовременное наблюдение (по времени регистрации фактов), т.к. проводилось только для данной партии товара;

-сплошное (по охвату единиц совокупности), т.к. проверялся весь товар из партии.

По способу статистического наблюдения – это непосредственное наблюдение, т.к. каждая единица товара подвергалась тщательному исследованию.

Задача 5.10.

Посредством случайной бесповторной выборки было обследовано 100 рабочих по стажу работы из общей численности 950 чел. На основе обследования был составлен ряд распределения:

Стаж работы, лет	До 5	5−10	10−15	15−20	20−25	Свыше 25	Итого
Количество рабочих	15	30	20	15	12	8	100

Определите с вероятностью 0,997, в каких пределах находится доля рабочих со стажем свыше 20 лет в общей численности рабочих по предприятию.

Решение.

По условию задачи имеем бесповторную, собственно-случайную, механическую выборку.

Из условия известно, что выборочная доля рабочих со стажем свыше 20 лет составляет

W = 20/100 = 0,2 или 20%.

Отсюда дисперсия доли равна:

σW2 =W (1 −W ) = 0,2 0,8 = 0,16 .

Т.к. обследовано 100

рабочих из 950, то

n

=

100

= 0,1053 , где n – объем выборочной

N

950

совокупности, N – объем генеральной совокупности.

При доверительной вероятности p = 0,997 коэффициент доверия t = 3. Тогда предельная

ошибка выборки равна:

= t

σW2

n

0,16

0,4

0,8947 = 0,1135 .

n

1 −

N

= 3

100

(1 −0,1053) = 3

10

W

Определим возможные пределы среднего значения доли рабочих со стажем свыше 20

лет в общей численности рабочих по предприятию:

W −

≤

≤W +

.

W

W

W

Подставив имеющиеся данные, получим

116

0,0947 ≤W ≤ 0,3135 или 9,47% ≤W ≤ 31,35% .

Т.е., с вероятностью 0,997 можно утверждать, что доля рабочих со стажем свыше 20 лет в общей численности рабочих по предприятию находится в пределах от 9,47% до 31,35%.

Задача 5.11.

Для установления среднего возраста 50 тыс. читателей библиотеки необходимо провести выборку из читательских карточек методом механического отбора. Предварительно установлено, что среднее квадратичное отклонение возраста читателей равно 10 годам. Определите необходимую численность выборки при условии, что с вероятностью 0,954 ошибка выборки будет не более трех лет. (Данные условные).

Решение.

Имеем собственно-случайную механическую выборку. Минимально необходимая численность выборки для бесповторного отбора определяется по формуле:

	n =	t 2	σ2 N	,
		2 N +t 2 σ2

где N = 50000 – общее количество читателей; t = 2 – коэффициент доверия для доверительной вероятности 0,954; σ = 10 – среднее квадратичное отклонение возраста читателей; = 3 – предельная ошибка выборки.

Подставив в расчетную формулу исходные данные, получим:

	n =	t 2	σ2 N	=	2	2 10	2 50000	= 44,4 .
		2 N +t 2 σ2			32	50000 + 22 102

Таким образом, необходимо проверить не менее 45 читателей.

Задача 5.12.

Из партии импортируемой продукции на посту Московской региональной таможни было взято в порядке случайной повторной выборки 20 проб продукта A. В результате проверки установлена средняя влажность продукта A в выборке, которая оказалась равной 6% при среднем квадратическом отклонении 1%. С вероятностью 0,683 (t = 1) определите пределы средней влажности продукта во всей партии импортируемой продукции.

Решение.

По условию задачи имеем: x = 6% , σ =1% , n = 20 .

По условию задачи имеем повторную выборку, следовательно, средняя ошибка выборки равна

117

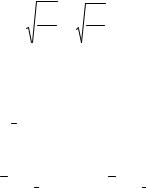
	μ =	σ2	=	1	= 0,2236 .
		n		20

При доверительной вероятности p = 0,683 коэффициент доверия t = 1. Тогда предельная ошибка выборки равна

x = t μ =1 0,2236 = 0,2236 .

Определим возможные пределы генеральной средней влажность продукта A: x − x ≤ M[x] ≤ x + x .

Подставив имеющиеся данные, получим

5,7764 ≤ M [x] ≤ 6,2236 .

Задача 5.13.

Каким должен быть объем случайной бесповторной выборки из генеральной совокупности численностью 10000 единиц при среднем квадратическом отклонении не более 20, предельной ошибке, не превышающей 5? И вероятности 0,997 (t = 3)?

Решение.

Необходимый объем выборки для случая бесповторного отбора равен

	n =	t 2	σ2 N	=	32 20	2 10000	=	36000000	=141,96	≥142	чел.
		2 N +t 2 σ2			52 10000 +32 202			253600

Задача 5.14.

Из 5% опрошенных выпускников университета 30% удовлетворены полученными знаниями за время обучения. Какова должна быть численность выборки, чтобы ошибка доли не превышала 0,05 (с вероятностью 0,954 и количестве выпускников 200 человек).

Решение.

Имеем собственно-случайную бесповторную выборку. Дисперсия доли равна

σW2 =W (1 −W ) = 0,3 0,7 = 0,21.

Минимально необходимая численность выборки определяется по формуле:

n =

t 2

σW2

N

=

2

2 0,21 200

=

168

=

168

=125,4

≥126

чел.

2W N +t 2 σW2

0,052 200 + 22 0,21

0,5 + 0,84

1,34

Задача 5.15.

118

В целях изучения затрат времени на изготовление одной детали рабочими завода проведена 10%-ная случайная бесповторная выборка, в результате которой получено следующее распределение деталей по затратам времени:

	Затраты времени на одну	Число деталей, шт.
	деталь, мин.
	До 20	10
	От 20 до 24	20
	От 24 до 28	50
	От 28 до 32	15
	Свыше 32	5
	Итого	100

На основании данных вычислите:

1.Средние затраты времени на изготовление одной детали.

2.Средний квадрат отклонений (дисперсию) и среднее квадратическое отклонение.

3.Коэффициент вариации.

4.С вероятностью 0,954 предельную ошибку выборочной средней и возможные границы, в которых ожидаются средние затраты времени на изготовление другой детали на заводе.

5.С вероятностью 0,954 предельную ошибку выборочной доли и границы удельного веса числа деталей с затратами времени на их изготовление от 20 до 28 мин.

Сделайте выводы.

Решение.

Приведем группировку к стандартному виду с равными интервалами и найдем середины интервалов для каждой группы. Результаты представлены в таблице:

Затраты времени на	Затраты времени на	Затраты времени на	Число
одну деталь, мин.	одну деталь, мин.	одну деталь, мин.	деталей, шт.
До 20	16 - 20	18	10
От 20 до 24	20 - 24	22	20
От 24 до 28	24 - 28	26	50
От 28 до 32	28 - 32	30	15
Свыше 32	32 - 36	34	5
	Итого		100

1. Средние затраты времени на изготовление одной детали определим по формуле средней арифметической взвешенной

119

y= ∑yi ni = ∑yi ni .

∑ni n

Подставив в последнюю формулу известные значения, получим средние затраты времени на изготовление одной детали

=

18 10 + 22 20 + 26 50 + 30 15 + 34 5

=

2540

= 25,4 мин.

y

100

100

2. Дисперсия определяется по формуле

∑( yi −

)2 ni

s

2

=

y

.

n

Подставив в последнюю формулу известные значения, получим дисперсию

s

2

(18 − 25,4)2 10 + (22 − 25,4)2 20 +K+ (34 − 25,4)

2 5

1484

2

=

=

=14,84 мин .

100

100

Среднее квадратическое отклонение равно

s =

s2

= 14,84 = 3,852 мин.

3. Коэффициент вариации определяется по формуле

v =

s

=

3,852

= 0,152 , или 15,2%.

25,4

y

4. Рассчитаем сначала предельную ошибку выборки. Так при вероятности p = 0,954 коэффициент доверия t = 2. Поскольку дана 10%-ная случайная бесповторная выборка, то

Nn = 0,1, где n – объем выборочной совокупности, N – объем генеральной совокупности.

Считаем также, что дисперсия σ y2 = s2 =14,84 . Тогда предельная ошибка выборочной средней равна

	= t	σ 2			n		14,84
		n	1	−		= 2	100	(1	− 0,1)	= 2 0,1484 0,9 = 0,731мин.
y
					N

Определим теперь возможные границы, в которых ожидаются средние затраты времени на изготовление одной детали на заводе

y − y ≤ my ≤ y + y , или 24,669 ≤ m y ≤ 26,131 .

Т.е., с вероятностью 0,954 можно утверждать, что средние затраты времени на изготовление другой детали на заводе находятся в пределах от 24,669 до 26,131 мин.

5. Выборочная доля w числа деталей с затратами времени на их изготовление от 20 до 28 мин. равна

w = 20100+ 50 = 0,7 = 70 %.

120

Учитывая, что при вероятности p = 0,954 коэффициент доверия t = 2, вычислим предельную ошибку выборочной доли

w = t	w(1 − w)	(1 −	n ) = 2	0,7 0,3	(1 − 0,1) = 2 0,00189 = 0,0869 , или 8,69%.
	n		N	100

Пределы доли признака во всей совокупности:

70% −8,69% ≤ d ≤70% +8,69%, или 61,31% ≤ d ≤ 78,69% .

Таким образом, с вероятностью 0,954 можно утверждать, что границы удельного веса числа деталей с затратами времени на их изготовление от 20 до 28 мин., находятся в пределах от 61,31% до 78,69% от всей партии деталей.

Выводы.

1.Так как коэффициент вариации меньше 33 %, то исходная выборка однородная.

2.Более двух третей деталей имеют время изготовления от 20 до 28 мин. Это свидетельствует о стабильной работе на заводе по выпуску данной детали.

Задача 5.16.

Для определения среднего срока пользования краткосрочным кредитом в банке была произведена 5%-ная механическая выборка, в которую попало 100 счетов. В результате обследования установлено, что средний срок пользования краткосрочным кредитом – 30 дней при среднем квадратическом отклонении – 9 дней. В пяти счетах срок пользования кредитом превышал 60 дней. С вероятностью 0,954 определить пределы, в которых будут находиться средний срок пользования краткосрочным кредитом в генеральной совокупности и доля счетов со сроком пользования краткосрочным кредитом более 60 дней.

Решение.

По условию задачи имеем бесповторную, собственно-случайную, механическую выборку.

1. Определим пределы, в которых будет находиться средний срок пользования краткосрочным кредитом.

Дисперсия и среднее срока пользования краткосрочным кредитом составляют соответственно σ2x = 9 2 = 81, x = 30 . Т.к. обследовано 5% счетов, то Nn = 0,05 , где n – объем

выборочной совокупности, N – объем генеральной совокупности.

При доверительной вероятности p = 0,954 коэффициент доверия t = 2. Тогда предельная ошибка выборки равна

121

= t

σ2x

n

81

=1,754 .

n

1

−

= 2

100

(1−0,05)

= 2

0,9 0,95

x

N

Определим возможные границы, в которых будет находиться средний срок

пользования краткосрочным кредитом:

−

≤ μx ≤

+

.

x

x

x

x

Подставив имеющиеся данные, получим

30 −1,754 ≤ μx

≤ 30 +1,754 , или 28,246 ≤ μx

≤ 31,754 .

2. Определим пределы, в которых будет находиться доля счетов со сроком пользования краткосрочным кредитом более 60 дней.

Выборочная доля счетов, у которых сроком пользования краткосрочным кредитом более 60 дней равна

W = 5/100 = 0,05, или 5%.

Отсюда дисперсия доли равна:

σW2

=W (1−W ) = 0,05 0,95 = 0,0475 .

Тогда предельная ошибка выборки равна:

= t

σW2

n

0,0475

= 0,0212 .

n

1−

= 2

100

(1−0,05)

= 2 0,000451

W

N

Определим возможные пределы, в которых будет находиться доля счетов со сроком

пользования краткосрочным кредитом более 60 дней:

W −

≤

≤W +

.

W

W

W

Подставив имеющиеся данные, получим

0,0288 ≤W ≤ 0,0712 , или 2,88% ≤W ≤ 7,12% .

Задача 5.17.

Заработная плата бригады характеризуется следующими данными:

	Профессия	Число	Месячная заработная плата
		рабочих	каждого рабочего, руб.
	Токари	4	1252; 1548; 1600;	1400
	Слесари	6	1450; 1380; 1260; 1700;	1250; 1372

Проверить правило сложения дисперсии и указать велико ли влияние профессии на различие в уровне заработной платы.

122

Решение.

Правило сложения дисперсии имеет вид:

s 2 = sмод2 + sост2 ,

где используются следующие дисперсии: общая sy2 , межгрупповая sмод2 и внутригрупповая

sост2 .

Средняя зарплата всех рабочих равна:

=

1

∑xi

=

1

(1252 +1548 +K+1372) =

14212

=1421,2 руб.

x

10

n

10

Общая дисперсия равна:

s 2 =

1

∑(xi −

) 2 =

(1252 −1421,2) 2 +K(1372 −1421,2) 2

=

215097,6

= 21509,76 .

x

n

10

10

Средняя зарплата токарей равна:

1 =

1

∑x1i =

1

(1252 +1548 +1600 +1400) =

5800

=1450 руб.

x

n

4

4

1

Средняя зарплата слесарей равна:

2 =

1

∑x2i =

1

(1450 +1380 +K1372) =

8412

=1402 руб.

x

n2

6

6

Межгрупповая дисперсия равна:

1

L

(1450 −1421,2)

2

4 + (1402 −1421,2)

2

6

5529,6

sмод2

=

∑(

x

i −

x

)2 ni =

=

= 552,96 .

10

n i=1

10

Дисперсия зарплаты токарей равна:

1

L

(1252 −1450)

2

+K

+(1400 −1450)

2

73808

s12 =

∑

(x1i −

1 ) 2 =

=

=18452 .

x

4

n

=

4

1

i 1

Дисперсия зарплаты слесарей равна:

1

n

(1450 −1402)

2

+K+(1372 −1402)

2

135760

s22 =

∑2

(x2i −

2 ) 2 =

=

= 22626,67 .

x

6

6

n2 i=1

Внутригрупповая дисперсия равна:

1

L

18452 4 + 22626,67 6

209568

sост2

=

∑si2 ni =

=

= 20956,8 .

n

i=1

10

10

Проверим правило сложения дисперсии:

sмод2

+ sост2

= 552,96 + 20956 ,8 = 21509 ,76 = s 2 , т.е. данное правило выполняется.

Определим влияние профессии на различие в уровне заработной платы. Расчетное значение F-отношения равно:

123

	ψ =	sмод2	=	552,96	= 0,026	,
		sост2		20956,8

это очень малое значение. Поэтому можно сделать вывод о том, что различие в профессии рабочих на их зарплату влияния практически не оказывает.

Задача 5.18.

В городе исследуются затраты времени жителей на ведение домашнего хозяйства. Опрошено 109 мужчин и 191 женщин. При этом выяснилось, что мужчины тратят в среднем 2,5 часа при среднем квадратическом отклонении 20 мин., а женщины – 3,5 часа при среднем квадратическом отклонении 10 мин. Найти 99% доверительный интервал для разности значений среднего времени, затрачиваемого женщинами и мужчинами на домашние работы.

Решение.

Выборка получена при бесповторном отборе. Отсюда предельные ошибки равны

- для мужчин

= t

s2

= 2,623

20

= 5,024 мин.;

x

0,01;107

x

10,440

n

1

- для женщин y

= t0,01;189

sy2

= 2,602

10

=1,883 мин.

n2

13,820

99% доверительный интервал для среднего времени, затрачиваемого мужчинами на

домашние работы равен

(

−

x ;

+

x ) = (150 −5,024; 150 +5,024) = (144,98; 155,02) .

x

x

99% доверительный интервал для среднего времени, затрачиваемого женщинами на

домашние работы равен

(

−

y ;

+

y ) = (210 −1,883; 210 +1,883) = (208,12; 211,88) .

y

y

99% доверительный интервал для разности значений среднего времени, затрачиваемого женщинами и мужчинами на домашние работы найдем как разность между двумя найденными доверительными интервалами для мужчин и женщин (в минутах)

( y − x − y − x ; y + x + y + x ) = (60 −1,883 −5,024; 60 +1,883 +5,024) = (53,09; 66,91) .

Задача 5.19.

Для анализа товарооборота магазинов города выборочным методом было проведено обследование 60% магазинов. Результаты выборки представлены в таблице (цифры условные):

124

Группы магазинов по		Число магазинов
товарообороту, тыс. руб.
До 50		4
50	– 60	6
60	– 70	8
70	– 80	7
80	– 90	12
90 – 100		22
100	– 110	18
110	– 120	10
120	– 130	8
Более 130		5

С вероятностью 0,997 определить для всех магазинов города пределы, в которых находится:

1)средний товарооборот;

2)доля магазинов с товарооборотом более 100 тыс. руб.

Решение.

1. Присвоим каждой группе значение среднегруппового товарооборота. В результате получим таблицу

Группы магазинов по	Число магазинов
товарообороту, тыс. руб.
45	4
55	6
65	8
75	7
85	12
95	22
105	18
115	10
125	8
135	5

Определим вначале выборочное среднее по формуле среднего арифметического взвешенного:

			∑xi ni		45 4 +55 6 +... +135 5		9380
	x =			=		=		= 93,8 тыс. руб.
			∑ni
					4 +6 +... +5		100

Отсюда выборочная дисперсия равна:

125

σ2			= ∑	(xi −	x	)2 ni	=	(45 −93,8)2 4 + (55 −93,8)2 6 +K+ (135 −93,8)	2 5	= 516,56 .
				∑ni
								100
По условию задачи имеем бесповторную, собственно-случайную, механическую
выборку. Т.к. обследовано 60% магазинов, то
	n		= 0,6 ,
	N

где n – объем выборочной совокупности, N – объем генеральной совокупности.

Средняя ошибка выборки равна
μ =	σ2		−	n	=	516,56	0,4	=1,4374 .
	n	1				100
				N

При доверительной вероятности p = 0,997 коэффициент доверия t = 3. Тогда предельная ошибка выборки равна

x = t μ = 3 1,4374 = 4,3123 .

Определим возможные пределы генеральной средней товарооборота

x − x ≤ M[x] ≤ x + x .

Подставив имеющиеся данные, получим

89,488 ≤ M[x] ≤ 98,112 .

2. Выборочная доля w магазинов с товарооборотом более 100 тыс. руб. равна:

w =	18 +10 +8 +5		= 0,41, или 41%.
		100
Учитывая, что при вероятности p = 0,997 коэффициент доверия t = 3, вычислим
предельную ошибку выборочной доли:
w = t		w(1 − w) (1 − n ) = 3		0,41 0,59 (1 −0,6)	= 0,0933 , или 9,33%.
		n	N	100
Пределы доли признака во всей совокупности:
41% −9,33% ≤ d			≤ 41% +9,33%, или 31,67% ≤ d ≤ 50,33% .

Задача 5.20.

Для определения среднего возраста планируется обследование населения города методом случайного поиска. Численность населения города составляет 1704000 человек. Каков должна быть необходимый объем выборочной совокупности, чтобы с вероятностью 0,954 ошибка выборки не превышала 5 лет при среднем квадратическом отклонении 25 лет.

Решение.

126

Необходимый объем выборки для случая бесповторного отбора равен

	n =	t 2	σ2 N	=	2	2 252 1704000	=100	чел.
		2 N +t 2 σ2			52 1704000 + 22 252

127