
Уравнение борна гринна ивонна (Уравнение бти) для парной корреляционной функции:
СВЯЗЬ МЕЖДУ РАЗЛИЧНЫМИ (по количеству переменных) ФУНКЦИЯМ РАСПРЕДЕЛЕНИЯ
![]() ,
,
![]() ,
,![]()
 ,
только в exp
есть зависимость от r1:
,
только в exp
есть зависимость от r1:
![]() ,
таким образом
,
таким образом
![]()
||
![]()
![]()
Теперь
найдем
![]()
UN=U12+U13+…+U23+U24+…
![]()

![]()
![]()
![]()
Одно из уравнений БТИ связывают функции распределения меньшего порядка с функциями распределения большего порядка (последующего).
БОГОЛЮБОВ-КИРКВУД: Предположим, что корреляция между тремя частицами осуществляется также парным образом:
g123 g12g13g23, тогда
![]() -
ББГКИ.
-
ББГКИ.
Делают
замену:
![]() ,
(V12
- это не объем!!!)
,
(V12
- это не объем!!!)
![]() ,
,
E13 - выражается через определенные производные от U13. Таким образом, мы свели уравнение к интегральному.
ЧИСЛЕННЫЕ МЕТОДЫ В ТЕОРИИ ЖИДКОСТИ.
Жидкая система - это система с сильным взаимодействием. Метод молекулярной динамики,
метод Монте-Карло.
Метод молекулярной динамики - попытка описать поведение из большего числа молекул основываясь на:
знании сил, действующих на частицу;
справедливости Ньютоновской механики для движения частиц;
эргодическая гипотеза
Система из N частиц:

![]() ,Ui
- потенциальная энергия, можно предположить
,Ui
- потенциальная энергия, можно предположить
парное
взаимодействие
![]()
![]() ,
зная НУ для каждой из частиц, можно найти
,
зная НУ для каждой из частиц, можно найти
![]() .
.
 Любое
состояние - точка с шестью координатами,
т.е. для каждой частицы
Любое
состояние - точка с шестью координатами,
т.е. для каждой частицы![]() ,т.е.
имеем 6N
- мерное пространство.
,т.е.
имеем 6N
- мерное пространство.
Плотность точек в фазовом пространстве дает вероятность
нахождения системы в данном состоянии. Можно ввести
статистическое распределение вероятности системы находиться в
некоторых состояниях.
ЭРГОДИЧЕСКАЯ ГИПОТЕЗА:
если взять точку, доступную системе и окружить её
окрестностью, то с течением времени фазовая кривая попадет в - окрестность любой точки в доступном фазовом объеме.
Все состояния системы при t будут достигнуты.
Введем бесконечное число систем, накладываем их друг на друга получаем "фазовый портрет" нашей макросистемы. Т.о. наберем много систем, находящихся в различном состоянии; понятно, что среди этих систем есть наиболее вероятностные, т.е. в какой то области плотность точек будет больше можно найти плотность вероятности, это называется УСРЕДНЕНИЕ ПО СТАТИСТИЧЕСКОМУ АНСАМБЛЮ.
Плотность вероятности величины f можно находить так:
можно усреднять по времени <f>
м
 ожно
усреднять по статистическому ансамблю.
ожно
усреднять по статистическому ансамблю.
Эргодическая гипотеза говорит, что эти два подхода равносильны.
Благодаря эргодической гипотезе можно утверждать, что мы можем получить вероятность каждого состояния
fn - плотность вероятности n-го состояния.
можно найти среднее величин в этих состояниях.
ТЕРМОДИНАМИЧЕСКИЙ
ПРЕДЕЛ
![]() при N
и
V
.
при N
и
V
.
Численные методы- попытка выстроить иерархию состояний системы- это метод молекулярной динамики.
Метод Монте-Карло- строит иерархию различных состояний системы, т.е. набор наиболее вероятных систем. Он не следит за временем, а составляет ансамбль.
МЕТОД МОЛЕКУЛЯРНОЙ ДИНАМИКИ.
Выделяется объем, по которому движутся частицы - куб со стороной l, в котором находится n частиц.

N ~103
l ~100Å
Все частицы первоначально бросаются в объем с произвольными
 .
Для каждой частицы пишется уравнение
Ньютона (II
закон F=ma),
.
Для каждой частицы пишется уравнение
Ньютона (II
закон F=ma),
но для этого надо знать системы, действующие на каждую частицу. Выбирается условная область вокруг частицы размером а0 (сфера, если в нее попадают другие частицы- то взаимодействие происходит, если не попадают- то не происходит; а0 d, т.е. взаимодействие с ближайшими соседями)
Считаем систему на частицу, берем малый промежуток t и решаем уравнение II закона Ньютона.
В
момент t
+ t
считаем
![]() (считаем, что ускорение не меняется) и
(считаем, что ускорение не меняется) и
![]()
Считается, что если частица вылетает из объема, то скорость частицы меняется на противоположную по направлению, т.е. заставляет её влетать
t ~ 10-14с.
В результате можно рассчитывать любые параметры характеризующие систему.
Предполагается, что температуру системы мы задаем.
Средняя
на молекулу кинетическая энергия:
![]()
подбираем начальные скорости так, чтобы
соответствовать этому условию.
подбираем начальные скорости так, чтобы
соответствовать этому условию.
![]()
![]()
Считается, что если |T| 1K, то всё в порядке, но если |T| > 1K, то ко всем скоростям добавляем или отнимаем V (в зависимости от знака T).


Любую функцию состояния системы можно рассчитать.
R - время релаксации - переход системы из
неравновесного в равновесное состояние.
" + ": Можно следить за установлением в системе равновесия, найти R .
" - " : 1) количество частиц никак не соответствует 1028. 103<<1028
2) маленький объем.
3) Твнешн задаем вручную (ничего не обосновано).
4) Время слежения на самом деле ограничено, т.к. t 10-14с.
5) Очень трудно решить задачу. Если молекулы не точечные, а имеют конечные размеры.
6) Невозможность учесть квантово-механические эффекты.
МЕТОД МОНТЕ-КАРЛО - найти распределение состояний системы.
Распределение вероятности нахождения системы
![]() ,
QN
- конфигурационный интеграл.
,
QN
- конфигурационный интеграл.
![]() .
.
Предположим, что вся система находится в кубе со стороной l~10Å. Куб делится на 4 ячейки, достаточно маленькие - l ~ d (расстояние между молекулами), т.е. в каждую ячейку по одной молекуле.
 N"1n"
~ 103.
N"1n"
~ 103.
Система может существовать и в другом состоянии N"n" ~ 103.
Задача метода - выстроить картину из череды состояний, т.е. построить ансамбль различных состояний системы и усреднить по нему.
![]()
Выбирается начальное состояние, следующее состояние по цепочке Мартова; новое состояние может быть хорошим ("+") и плохим("-"). Плохие мы отбрасываем.
Иерархия строится так:
задается первое состояние;
берем одну молекулу и перекладываем её в другую ячейку;
- получаем новое состояние; его мы можем либо принять, либо отвергнуть.
Если Uij (изменение энергии системы за счет перехода молекулы из состояния i в j) меньше 0, то состояние "хорошее".
Если
же Uij
<
0,
![]() -
вероятность перехода из состояния iв
j (считаем, что Т задано).Pij
< 1;
если
<
Pij,
тогда
берём;
-
вероятность перехода из состояния iв
j (считаем, что Т задано).Pij
< 1;
если
<
Pij,
тогда
берём;
если > Pij, то отбрасываем.
Таким образом строим систему различных состояний (в принципе, она должна быть бесконечной), получаем распределение вероятности системы находиться в некоторых состояниях.
" - ": 1) ограниченность числа молекул и пространства;
2) сама процедура определения "хорошего" и "плохого";
3) момент выбора частицы, которая должна переходить из состояния в состояние;
4) не можем следить за системой с течением времени.
" + ": 1) элементарно учитывается конфигурация молекулы (размером ячейки);
2) можно учесть квантово-механические требования (например, два электрона не могут находиться в одном состоянии);
3) изначально система в термодинамическом равновесии.
=============================03.12.2002=======================================
Н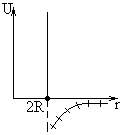 евзаимодействующие
шары:
евзаимодействующие
шары:
Нет притяжения,
поэтому непонятен
скачок в P-

-Как будто
происходит
фазовый F = U - TS, если система на каком-то
 переход
этапе
переход
этапе
Мы бы всё объяснили, если бы доказали, что

Чем больше S, тем больше F, тем
благоприятнее состояние.
( * )
 Когда
плотность газа из частиц круглых мала,
то число конфигурационных состояний
велико, а когда
большое, то число конфигурационных
состояний меньше.
Когда
плотность газа из частиц круглых мала,
то число конфигурационных состояний
велико, а когда
большое, то число конфигурационных
состояний меньше.

S1conf
> S2conf,
т.е.
S1conf
> S2conf,
т.е.
Но молекулы не точечные, значит для них нужно учитывать исключенный объем (здесь он связан так- за исключением самих молекул объем системы Vexcluded= Vсист - Vшаров).
Тогда SLexcl > SVexcl (связано с вероятностью того, что при попадании в объем системы мы наткнемся на исключенный объем). Исключенный объем в случае L распределен более равномерно.
мы объяснили график ( * ).
ВЗАИМОДЕЙСТВИЕ МАКРОСКОПИЧЕСКИХ ТЕЛ.
![]()
 ,
с учетом запаздывания:
,
с учетом запаздывания:
![]()
Взаимодействие за счет сил межмолекулярного взаимодействия -
молекулы одного тела взаимодействуют с молекулами другого.
Представим, что одно из тел имеет плоскую границу:
р адиус
межмолекулярных сил очень не велик,
поэтому границу
адиус
межмолекулярных сил очень не велик,
поэтому границу
можно полагать плоской.
Посмотрим, с какой силой молекула находится на расстоянии l
от тела, взаимодействует с телом. Начало координат в точке
нахождения молекулы.
dN = ndV - число молекул в dV, n - концентрация.
![]() - сила о одной молекулы к другой (их
взаимная сила взаимного объемаdV
и нашей молекулы) в сферических
координатах:
- сила о одной молекулы к другой (их
взаимная сила взаимного объемаdV
и нашей молекулы) в сферических
координатах:
df
= ?
![]() ,
,
0 m
l r <
0 < < 2
dN = r2sin dddr
f -суммарная сила.
![]()

 -
сила, с
-
сила, с
которой одна молекула притягивается к другой с такой границей.
Теперь два тела
 Возьмем
элементарный объемdV
Возьмем
элементарный объемdV
dV = Sdx
dNB = nBSdx
![]()
полная
сила
![]()
![]() ,
,
с
учетом запаздывания
![]()
 Для
тел конечной кривизны:
Для
тел конечной кривизны:
R1>>h
R2>>h
![]() F
= -grad U
F
= -grad U
![]()
Гамакер ввел формулу для двух сфер с помощью своих вычислений:
![]()

прослойка не вакуум, диэлектрическая проницаемость с >1.
На
малых
![]() ,
на больших
,
на больших![]() .
Если у А и В разные диэлектрические
свойства, то
.
Если у А и В разные диэлектрические
свойства, то![]() !!
!!
н
 еполярная
жидкость. Плёнке выгодно разбухнуть,
т.е. превратиться в шар.
еполярная
жидкость. Плёнке выгодно разбухнуть,
т.е. превратиться в шар.
============================================================================
ВЗАИМОДЕЙСТВИЕ МАКРОСКОПИЧЕСКИХ ТЕЛ, ПОМЕЩЕННЫХ В ЖИДКИЙ ЭЛЕКТРОЛИТ (ЖИДКОСТЬ, В КОТОРОЙ ЕСТЬ РАЗРЯЖЕННЫЕ ИОНЫ).
Образование двойного электрического слоя:
 zi
- зарядовое
число иона.
zi
- зарядовое
число иона.
![]()
Так как суммарный заряд всех ионов должен быть равен нулю, заряд объема

![]() -
полный заряд единичного объема.
-
полный заряд единичного объема.
Если в жидкости есть какие-то примеси, в ней и обязательно есть и ионы. Предположим, что в такую жидкость помещается макроскопическое тело. Оно не электронейтральное из-за некоторого массообмена, почти всегда присутствующего в такой системе диффузных электронов, диффузия- адсорбция электронов (они усаживаются на тело), может быть какое -то трение, или специальная электролитация, следовательно на поверхности тела возникает некий избыточный поверхностный заряд, он может быть как положительным, так и отрицательным.
 В
результате возникновения поверхностного
зарядаq0
В
результате возникновения поверхностного
зарядаq0
возникает и поверхностный потенциал 0. Ионы, отличающиеся
по знаку, от знака поверхностного заряда называют
противоионами, а ионы, заряд которых такой же по знаку как и
у поверхностного, называют коионами.
 Возникает
система, называемая двойным
Возникает
система, называемая двойным
электрическим слоем. Этот слой зависит от q0 и 0. Область,
где сконцентрирован заряд поверхности, называется плотной
частью двойного электрического слоя, а участок, который
идет за ним-диффузный участок двойного электрического слоя.
![]() -
-
- условие электронейтральности раствора.
условие электронейтральности раствора.
Описание двойного электрического слоя:
Плотность заряда по определению
![]() ,
,
где qi и ni - соответственно заряд и концентрация i-того иона.
Уравнение
электростатики
![]() ,
,![]() .
Если предположить, что
не зависит от z,
то
.
Если предположить, что
не зависит от z,
то
![]() ,
кроме того, мы знаем, что
,
кроме того, мы знаем, что
![]()
![]() -
уравнение Пуассона.
-
уравнение Пуассона.
![]() .
.
![]() - предположение, что ионы находятся в
тепловом равновесии и справедливо
распределение Больцмана.
- предположение, что ионы находятся в
тепловом равновесии и справедливо
распределение Больцмана.
В конечном случае:
![]()
Wi - потенциальная энергия иона, можно сделать предположение Wi qii(z) (т.е. считаем, что только тот потенциал от поверхности создает Wi, не учитываем взаимодействие между ионами).
Тогда
![]() -
-
уравнение Пуассона-Больцмана в приближении Гуи- Чепмана.
(z = 0) = 0, (z ) = 0.
Можно
сделать разложение, предположив, что
![]() - предположение Дебая -Хюкени.
- предположение Дебая -Хюкени.
![]()
Тогда из Пуассона-Больцмана:
![]()
 ,
или переобозначив
,
или переобозначив
![]() (решение
в одномерном случае
(решение
в одномерном случае![]() )
)
![]() ,
,![]() - дебаевский радиус,
- дебаевский радиус,
Т о
есть вблизи поверхности потенциал
падает и эффективно он падает на
расстоянии дебаевского радиуса (т.е.
это размер двойного электрического
слоя).
о
есть вблизи поверхности потенциал
падает и эффективно он падает на
расстоянии дебаевского радиуса (т.е.
это размер двойного электрического
слоя).
