Переход к хаосу

Пути возникновения хаоса.

Хаос определяют как состояние беспорядка и нерегулярности. Рассматриваются физические системы, поведение которых во времени детерминированно, т.е. существует правило в виде дифференциальных или разностных уравнений, определяющее их будущее исходя из заданных начальных условий.

А.Пуанкаре открыл, что в некоторых механических системах (эволюция которых определяется уравнениями Гамильтона) может появляться хаотическое движение. До этого считалось, что детерминированное движение достаточно регулярно и далеко от хаотичности,

поскольку последовательные состояния непрерывно развиваются одно из другого. Все это не воспринималось серьезно до тех пор, пока в 1963 г. метеоролог Е.Н.Лоренц не обнаружил, что простая система из трех связанных нелинейных дифференциальных уравнений первого порядка может привести к совершенно хаотическим траекториям.

Под детерминированным хаосом подразумевается нерегулярное или хаотическое движение, порожденное нелинейными системами, для которых динамические законы однозначно определяют эволюцию состояния системы во времени при известной

предыстории.	Нелинейность – необходимое, но не достаточное условие для возникновения
хаотического	движения.

Хаос возникает не из-за внешних источников шума, не из-за бесконечного числа степеней свободы. Настоящая первопричина – свойство нелинейных систем экспоненциально быстро разводить первоначально близкие траектории в ограниченной области фазового пространства.

Практически невозможно предсказать длительное поведение таких систем, поскольку реально начальные условия можно задать лишь с конечной точностью, а ошибки экспоненциально нарастают.

Если пытаться решить такую нелинейную систему на ЭВМ, результат на все более дальних временах зависит от все большего количества цифр в числах, представляющих начальные условия. Так как цифры в иррациональных числах распределены нерегулярно,

траектория становится хаотической.

Детермированность подразумевают однозначную взаимосвязь причины и следствия. Если задано некоторое начальное состояние системы при t = t0 , то оно однозначно определяет состояние системы в любой момент времени t > t0 . Если мы говорим о хаосе, мы подразумеваем,

что изменение во времени состояния системы является случайным (его нельзя однозначно предсказать) и невоспроизводимым (процесс нельзя повторить).

Режим функционирования динамической системы называют устойчивым, если малые возмущения затухают во времени, стремясь к нулю. Если этого не происходит и малые отклонения от режима функционирования системы нарастают во времени, такой режим будет неустойчивым.

Основным свойством динамических систем, демонстрирующих режим детерминированного хаоса, является чувствительная зависимость режима функционирования

к сколь угодно малым изменениям начальных условий. Именно это обстоятельство ведет к

потере детерминированной предсказуемости и необходимости вводить вероятностные характеристики для описания динамики таких систем. В этом смысле становится понятным

термин детерминированный хаос, который характеризует рождение случайного,

непредсказуемого поведения системы, управляемого детерминированными законами.

Пути возникновения хаоса.

Анализируем эволюцию диссипативных систем, т.е. систем, приводящих к необратимым процессам.

d X (t ) F ( x t ) - если рассматривается непрерывный случай. dt

x k 1 f ( x k ) - если рассматривается отображение с дискретным временем.

X R m - вектор m-мерного пространства.

F - включает управляющие параметры, определяющие связи с окружающей средой, изменение которых определяет поведение всей системы.

Если системы диссипативные, то траектории всегда сходятся к аттрактору (точки притяжения).

Будем называть динамический режим хаотическим, если спектр мощности содержит широкую полосу независимо от возможного наличия пиков.

Автокорреляционная функция временного сигнала обращается в ноль на некотором конечном интервале времени. Это говорит о потере сигналом памяти о самом себе.

В 1971 году Рюэль и Таккенс ввели понятие странный аттрактор и показали, что для возникновения хаоса достаточно трех степеней свободы.

Странный аттрактор – аттрактор, топологически отличный от тора. Одним из основных свойств странного аттрактора является чувствительная зависимость от начальных условий – ЧЗНУ.

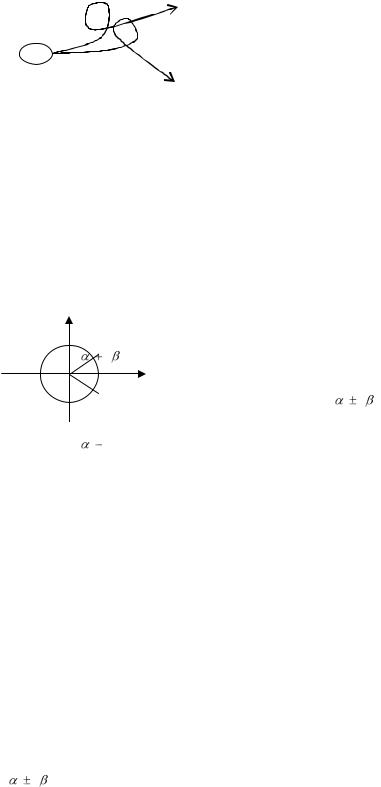
Следствие ЧЗНУ – обращение в ноль автокорреляционной функции и широкополосный спектр Фурье.

н.у.

Индексом этого разбегания является показатель Ляпунова

Задача. Определим	условия, при которых система переходит от регулярного режима к
хаотическому (потеря	периодичности – когда периодический процесс теряет устойчивость).

Потеря устойчивости периодическим движением, сопровождаемым возникновением бифуркации, происходит тогда, когда одна из кривых, при изменении параметра 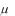, выходит за пределы единичной окружности.

	Im		Есть три возможных варианта потери
		i	периодичности – пути к хаосу:
-1	1	Re	-1, +1,	i

i

Три пути потери периодичности:

Точка пересечения с	Бифуркация		Явление
окружностью
+1	Седло-узел		Перемежаемость	первого
			рода
-1	Субгармоническая:	либо	Субгармонический каскад
	нормальная (суперкритическая);		Перемежаемость	третьего
	либо обратная (субкритическая).
			рода
i	Хопфа: Нормальная;		Квазипериодичность
	Обратная.		Перемежаемость	второго
			рода

Точка (+1) :

При пересечении единичной окружности в точке +1возникает бифуркация седло-узел.

Периодическое движение становится не только неустойчивым, но и полностью исчезает. В

области, параметра немного выше порога бифуркации, наблюдается перемежаемость первого типа. Это фазы регулярного, почти периодического, поведения (ламинарное движение), которые время от времени прерываются турбулентными всплесками (турбулентное = хаотическое движ.)

Точка (-1):

Субгармоническая суперкритическая бифуркация.- новое устойчивое периодическое решение с удвоенным периодом замещает старое, которое становится неустойчивым. Удвоение периода повторяется каждый раз, когда возникает новое периодическое движение, что приводит к бесконечной последовательности бифуркаций, называемой субгармоническим каскадом,

заканчивающейся хаосом.

Субкритическая бифуркация приводит к перемежаемости третьего типа, длинные фазы периодического движения нарушаются хаотическими всплесками. Это похоже на перемежаемость первого типа. Отлчие в том, что тип III характеризуется монотонным увеличением амплитуды субгармоники на протяжении почти периодической фазы из-за того, что все нелинейные эффекты усиливают субгармоническую неустойчивость предельного цикла.

Амплитуда возрастает с каждым колебанием . Постоянно увеличиваются пики - субгармоники,

то есть амплитуды сигналов.

Точки 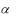i :

Неустойчивость третьего типа возникает, когда два комплексно сопряженных значения 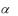i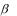

одновременно пересекают единичную окружность. Это бифуркация Хопфа. При нормальной бифуркации приходит к устойчивому аттрактору вблизи предельного цикла, затем предельный цикл сам становится неустойчивым. Этот аттрактор – тор T 2 , на поверхности которого лежит новое решение, соответствующее новому квазипериодическому режиму (две частоты - две основные гармоники).

Обратная бифуркация приводит к порождению странного аттрактора. Перемежаемость второго типа имеет частоту ламинарной фазы, несвязанную с основной частотой предельного цикла.

Как известно, в уравнениях динамических систем обычно присутствуют параметры – величины,

которые считаются постоянными во времени, но от задания которых может зависеть характер реализующегося в системе режима. Можно представить себе, что система заключена в черный ящик, на котором имеется несколько ручек настройки. Предположим, что при одном положении ручек наблюдается регулярный режим динамики, например, периодические колебания, а при другом – хаос. Если мы плавно меняем настройку так, чтобы перейти от первой ситуации ко второй (рис. 1), то какой будет на пути к хаосу последовательность бифуркаций – событий,

состоящих в качественном изменении характера наблюдаемого режима? Об этой последовательности бифуркаций принято говорить как о сценарии перехода к хаосу. При этом подразумевается, что имеется сравнительно немного сценариев, являющихся в определенном смысле слова типичными, так что проблема их классификации и изучения не является необозримой.

рис. 1. К понятию сценариев перехода к хаосу

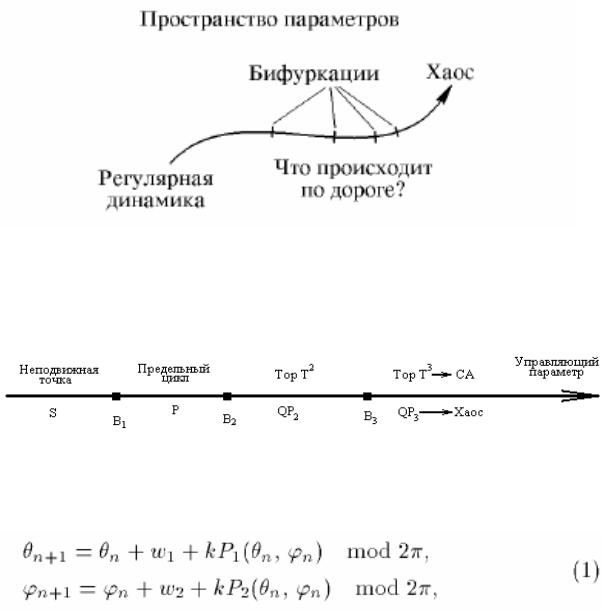
В работе Grebogi et al.[6], 1985 был предпринят численный эксперимент с модельной системой,

описывающей динамику с тремя несоизмеримыми частотами:

где переменные θ и φ имеют смысл фаз, одна частота отвечает шагу дискретного времени, а

вторая и третья задаются, соответственно, параметрами ω1 и ω2 . Функции P1(θ; φ) и P2(θ; φ)

имеют период 2π по каждому аргументу и представляются рядами Фурье. Была проведена большая серия расчетов. Задав величины коэффициентов Фурье и параметры ω1 и ω2 случайным образом, исследователи определяли характер реализующегося режима по показателям Ляпунова:

*Λ < 0 – периодический,

*Λ1 = 0, Λ2 < 0 – 2-x частотный квазипериодический, 2-тор,

*Λ1 = 0, Λ2 = 0 – 3-х частотный квазипериодический, 3-тор,

*Λ1 > 0 – хаос.

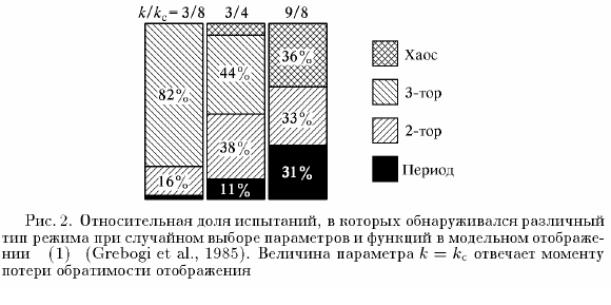
На рис. 2 приведена диаграмма, где сопоставляется относительная доля испытаний, в которых обнаруживался тот или иной тип режима. При малом уровне возмущения k доминирует трехчастотная квазипериодичность. С ростом уровня возмущения растет доля периодических и хаотических режимов. При k > kс, где kс отвечает моменту потери обратимости модельного отображения, трехчастотная квазипериодичность становится невозможной.

В 1980 г. появилось сообщение французских исследователей И.Помо и П. Манневилля,

положившее начало изучению группы сценариев перехода к хаосу через перемежаемость. В

гидродинамике давно известна так называемая перемежающаяся турбулентность, когда течение в определенных пространственных областях имеет плавный, ламинарный характер, но они чередуются с областями нерегулярного, турбулентного течения. Благодаря тому, что турбулентные области перемещаются, меняют форму, возникают и исчезают, перемежающийся

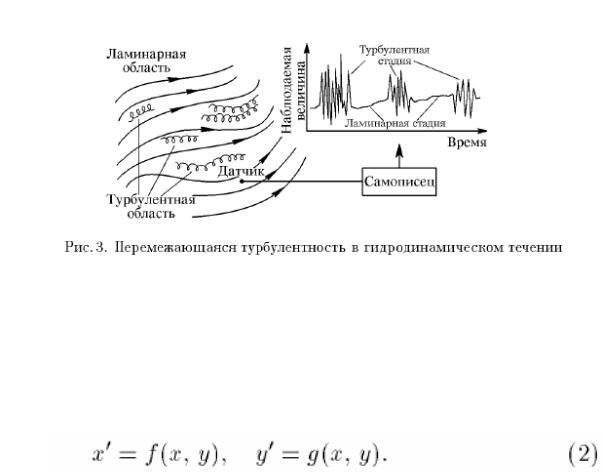
характер носит также зависимость наблюдаемых величин от времени в фиксированной точке пространства (рис. 3). Помо и Манневилль указали несколько возможных ситуаций, когда в ди-

намических системах (в том числе со сравнительно небольшой размерностью фазового пространства) может возникнуть перемежаемость, и наметили классификацию, введя в

рассмотрение три типа перемежаемости.

Итак, в итоге изучения вопроса о переходе динамических систем к хаосу сложилось представление о трех основных сценариях, а именно: через каскад удвоений периода,

перемежаемость и квазипериодические режимы.

Предположим сначала, что в системе реализуется простейший устойчивый периодический режим динамики, т. е. предельный цикл. Чтобы увидеть, что с ним может произойти при изменении параметров, воспользуемся методом сечения Пуанкаре. Пусть для простоты цикл

«живет» в трехмерном фазовом пространстве, тогда имеем двумерное отображение Пуанкаре

Точка, где предельный цикл протыкает поверхность сечения, есть неподвижная точка этого отображения: x0 = f(x0 ; y0), y0 = g(x0 ; y0). Исследование на устойчивость заключается в том, что мы подставляем в (2) x = x0 + x˜, y = y0 + y˜ и, удерживая члены первого порядка,

получаем

Если ввести след и детерминант матрицы Î, соответственно,

то собственные числа получаются как корни квадратного уравнения

А именно,

Произвольный вектор возмущения представляется в виде линейной комбинации двух собственных векторов. При каждом обходе предельного цикла возмущение, отвечающее каждому собственному вектору, умножается на соответствующее собственное число – мультипликатор μ. Поэтому цикл устойчив, если оба мультипликатора по модулю меньше единицы, и неустойчив, если хотя бы один мультипликатор по модулю больше единицы. Две пограничные линии области устойчивости на плоскости (S; J) можно получить из (6), полагая μ = 1 или μ = – 1, что дает, соответственно,

Третья пограничная линия находится из соотношения (7): если под знаком квадратного корня стоит отрицательное число, то модуль мультипликатора будет единичным при

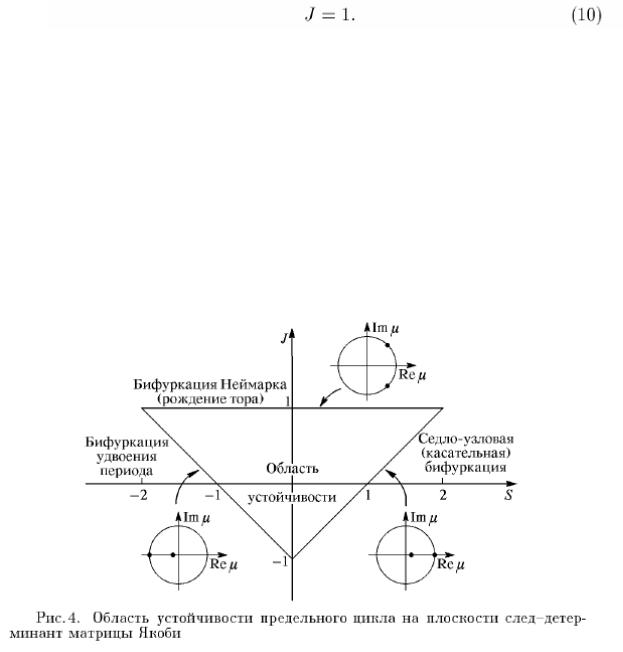
Область внутри треугольника, образованного линиями (8)-(10), есть область устойчивости.

Предположим, что наша система содержит параметр А. Когда мы варьируем этот параметр, будут изменяться координаты неподвижной точки хо, уо, и, соответственно, след и детерминант матрицы Якоби: S = S(A), J = J (А). При этом на плоскости (S, J) мы будем двигаться вдоль некоторой кривой. Ясно, что типичным надо признать выход из треугольника устойчивости через одну из его сторон (рис. 4).

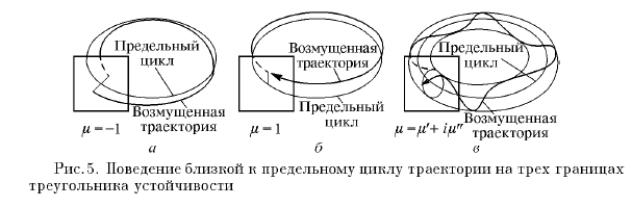
Предположим сначала, что выход осуществляется через левую границу треугольника. На пороге потери устойчивости мультипликатор равен минус единице. Это значит, что при однократном обходе цикла малое возмущение меняет знак (рис. 5). Чтобы траектория замкнулась, нужно совершить еще один обход, так что период вновь возникшего движения оказывается вдвое больше, чем у исходного.

Если присущая системе нелинейность такова, что при увеличении амплитуды возмущения происходит его стабилизация, то результатом бифуркации будет рождение цикла с периодом,

вдвое большим исходного. Это бифуркация удвоения периода. Очень часто при дальнейшем изменении параметра за ней вновь следуют бифуркации такой же природы. Последовательность бифуркационных значений параметра накапливается к определенному пределу, критической

точке, которая является в определенном смысле границей хаоса. Это сценарий перехода к хаосу через каскад бифуркаций удвоения периода — сценарий Фейгенбаума.

Может встретиться другая ситуация, когда нелинейность способствует ускорению роста возмущения и уходу системы от ставшей неустойчивой периодической орбиты. В этом случае,

когда

мы подходим к точке бифуркации, к рассматриваемому циклу приближается неустойчивый цикл удвоенного периода, который сливается с исходным циклом в точке бифуркации и, как говорят,

передает ему свою неустойчивость. После бифуркации наблюдается уход близлежащих траекторий от неустойчивого цикла в удаленные области фазового пространства. Может случиться, что динамика в этих удаленных областях такова, что через некоторое время траектория возвращается в окрестность неустойчивого цикла, тогда она останется вблизи него в течение некоторого времени, вновь уйдет, затем вновь вернется и т. д. Если такая реинжекция траектории в окрестность неустойчивого цикла имеет место, и если динамика в удаленных областях фазового пространства характеризуется наличием неустойчивости по отношению к возмущению начальных условий, то это приводит к возникновению хаотического режима перемежающегося типа. Помо и Манневилль обозначают его как перемежаемость типа III.

Рассмотренные варианты бифуркаций наглядно иллюстрируются с помощью одномерных отображений (рис. 6 и 7). Такая возможность связана с тем, что анализируемая граница потери устойчивости пересекает ось J = О, которую можно трактовать как соответствующую случаю одномерных отображений.