lek2

Продифференцировав это уравнение по времени, можно получить связь между линейной скоростью каждой точки тела с его угловой скоростью:

v = dS = dϕ r = ω r , dt dt

v = ω r .

Линейная скорость движения точки по окружности равна произведению угловой скорости на радиус окружности.

МОМЕНТ ИМПУЛЬСА МАТЕРИАЛЬНОЙ ТОЧКИ

Если материальная точка движется со скоростью v относительно некоторой системы отсчета, то она обладает не только импульсом mv , но и моментом импульса относительно точки 0 – начала координат.

Момент импульса материальной точки – это вектор, равный векторному произведению радиуса – вектора r материальной точки m на вектор ее импульса mv :

L

Вектор момента импульса

	mv			r	r	r
				L = r		× mv
l			α
0		r	m	l – плечо импульса

r

Вектор L момента импульса как результат векторного произведения перпендикулярен векторам – множителям r и mv , а его направление определяется по правилу буравчика ( см. рисунок).

r

Модуль вектора L равен произведению модуля вектора r на модуль вектора mv и на синус угла между ними. На рисунке это угол α.

r	=	r		r	sin α	.
L		r		mv

Как видно из рисунка, l – длина перпендикуляра, опущенного из начала координат на прямую, вдоль которой направлен импульс материальной точки. Этот перпендикуляр, а точнее его длина, называется плечом импульса. В образовавшемся прямоугольном треугольнике этот перпендикуляр находится напротив угла, смежного с углом α, следовательно, плечо импульса равно

l =	r	sin(1800			− α )=	r	sin α .
	r					r
Заменив в уравнении для модуля			r	произведение				r	sin α	на l, получим важ-
			L					r

ное правило: модуль момента импульса материальной точки равен про- изведению модуля ее импульса на плечо:

r

L = mvl .

Пусть материальная точка движется по окружности радиуса r вокруг оси 0z, перпендикулярной этой окружности и проходящей через ее центр. В этом случае проекция момента импульса этой материальной точки на ось 0z будет равна произведению ее импульса на радиус окружности. В этом случае радиус будет плечом импульса.

Lz = mvr .

МОМЕНТ СИЛЫ Пусть момент импульса материальной точки изменяется со временем.

Возьмем производную от момента импульса по времени.

r

r

r

r

r

dL

d

r

r

dr

r r

dv

r

r r

r

r

r

=

(r

× mv ) =

× mv

+ r

× m

= v

× mv + r

× ma

= 0

+ r

× F

= r

× F .

dt

dt

dt

dt

Векторное произведение

r

r

r

r

× F

называется моментом силы M :

r

r

r

.

M = r

× F

Окончательно получим

	dL	r
		= M .

dt

Итак, производная от момента импульса материальной точки по времени равна моменту силы, действующей на эту точку.

Как и в случае вектора момента импульса, можно показать, что модуль вектора момента силы равен произведению силы на ее плечо:

M = F l .

Следовательно, чтобы изменить момент импульса материальной точки только силы недостаточно. У этой силы должно быть плечо!

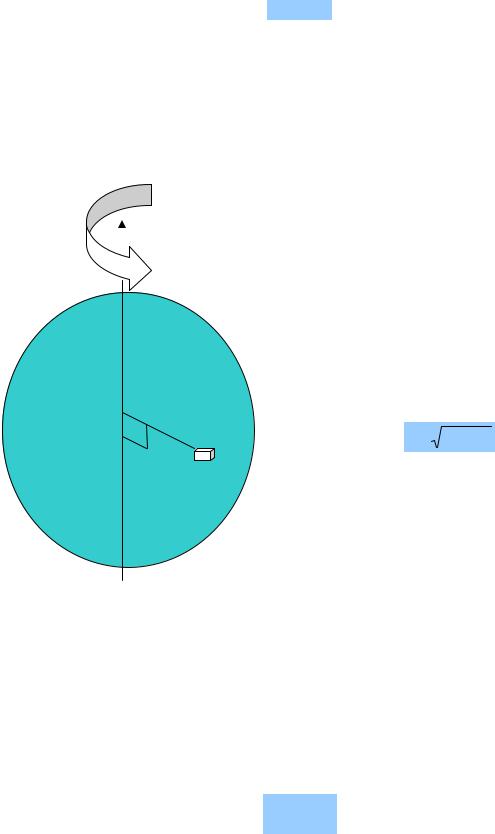
МОМЕНТ ИМПУЛЬСА ТВЕРДОГО ТЕЛА. МОМЕНТ ИНЕРЦИИ Абсолютно твердое тело состо-

ит из бесчисленного множества мате-

z

риальных точек массы dm. Если это ω тело вращается вокруг оси 0z, то каждая материальная точка движется по окружности, расположенной в плоскости (x; y), а радиус этой ок-

ружности равен

0	r	r = x 2	+ y 2 .
	dm

Проекция момента импульса твердого тела на ось 0z будет равна сумме проекций моментов импульсов каждой материальной точки тела,

то есть сумме бесконечно большого числа бесконечно малых слагаемых. Такая сумма является интегралом, который нужно взять по всему объему тела.

Lz = ∫dm v r = ∫dm ω r 2 = ω ∫r 2 dm .

V V V

Последний интеграл называется моментом инерции тела относительно оси 0z:

I = ∫r 2 dm .

V

Величина этого интеграла зависит от распределения массы внутри твердого тел относительно оси вращения. Итак, момент импульса твердого тела от-

носительно оси вращения равен произведению момента инерции этого тела относительно этой оси на угловую скорость вращения тела:

Lz = I z ω .

Путем интегрирования по объему тела можно получить формулы для вычисления момента инерции данного тела:

I = ml 2 – момент инерции материальной точки относительно оси, отстоящей от нее на расстоянии l;

I = mR 2 – момент инерции полого цилиндра массы m и радиуса R относительно оси этого цилиндра;

I = mR 2 момент инерции сплошного однородного цилиндра массы m и ра-

2

диуса R относительно оси этого цилиндра.

УРАВНЕНИЕ ДИНАМИКИ ДЛЯ АБСОЛЮТНО ТВЕРДОГО ТЕЛА

Пусть момент импульса твердого тела изменяет-

ся. Возьмем производную по времени от момента им-

M

пульса, выраженного через произведение момента инерции тела на угловую скорость:

ω	dLz	= I			dω	= I		ε	.
			z				z
	dt				dt

С другой стороны эта производная равна моменту силы, действующей на тело:

dLz = M z . dt

Сравнив эти два уравнения, получим

I z ε = M z

– произведение момента инерции твердого тела относительно некоторой оси на его угловое ускорение равно моменту силы относительно этой оси, действующей на тело. Последнее уравнение является уравнением динамики твердого тела или уравнением второго закона Ньютона для твердого тела.

ЗАКОН СОХРАНЕНИЯ МОМЕНТА ИМПУЛЬСА Вектор момента импульса системы тел равен сумме векторов моментов

импульса всех тел системы, а проекция вектора момента импульса системы тел на ось 0z равна сумме проекций векторов моментов импульса всех тел системы на эту ось:

Lz = ∑Lzi .

i

Производная по времени от проекции вектора момента импульса системы тел на ось 0z будет равна сумме проекций на ось 0z всех моментов сил, как внутренних, так и внешних:

dLdtz = ∑(Fz )внш + ∑(Fz )внтр .

Но все внутренние силы попарно являются взаимно противоположными векторами и имеют одинаковые плечи. Следовательно, суммарный момент всех внутренних сил равен нулю. А это значит, что производная по времени от проекции вектора момента импульса системы тел на ось 0z будет равна сумме проекций на ось 0z только всех моментов внешних сил:

dLdtz = ∑(Fz )внш .

Следовательно, только внешние силы могут изменить момент импульса системы тел.

Таким образом, если внешние силы на систему не действуют, то есть она является замкнутой, то момент импульса такой системы не изменяется, то есть сохраняется.

Мы получили закон сохранения момента импульса: момент им-

пульс замкнутой системы не изменятся, какие бы взаимодействия и превращения ни происходили бы внутри этой замкнутой системы.

Если моменты внешних сил компенсируют друг друга, то момент импульса системы также не изменяется.

Внимание!!! Если известно, что импульс системы сохраняется, а это будет в тех случаях, если система замкнутая или если внешние силы компен-

сируют друг друга, то момент импульса сохраняется только, если система замкнутая. Ведь у внешних сил могут быть разные плечи, и эти моменты не будут компенсировать друг друга. И наоборот, из сохранения момента им-

пульса системы не всегда следует, что и импульс ее сохраняется.

Уравнение закона сохранения момента импульса для системы взаимодействующих тел следует записывать следующим образом:

L1 + L2 = L1' + L'2 ,

гдеL1 и L2 – моменты импульса тел системы до взаимодействия, а L1' и L'2 –

моменты импульса этих тел после взаимодействия.

Уравнение закона сохранения момента импульса для твердого тела следует записывать следующим образом:

ω1 I1 = ω 2 I 2 ,

где ω1 I1 – момент импульса тела до взаимодействия, а ω 2 I 2 – после взаимо-

действия.

ДВИЖЕНИЕ СПУТНИКА Спутник движется под действием гравитационной силы вокруг некото-

рого центрального массивного тела по эллипсу. При этом сила гравитационного притяжения все время направлена к центру. Поэтому она не имеет плеча и не может изменить момент импульса спутника. Таким образом, к спутнику можно применить закон сохранения момента импульса:

r	r	r	r	.
r1	× mv1	= r2	× mv2

КИНЕТИЧЕСКАЯ ЭНЕРГИЯ ТВЕРДОГО ТЕЛА Выражение для кинетической энергии вращающегося абсолютно твер-

дого тела получим путем интегрирования по всему объему тела выражения для кинетической энергии материальной точки массы dm – маленького кусочка твердого тела:

E =	∫	dm v 2	=	∫	ω 2 r 2 dm =	Iω 2	.
		2
k					2
	V			V

Если твердое тело и движется поступательно, и вращается, то его кинетическая энергия состоит из двух слагаемых: кинетической энергии поступательного движения и кинетической энергии вращательного движения.

E		=	mv 2	+	Iω	2	.
	k		2		2

В заключение приведем сравнительную таблицу пар физических величин, являющихся аналогами в кинематике и динамике материальной точки и кинематике и динамике абсолютно твердого тела.

Материальная точка				Твердое тело
Масса		m		Момент инерции			I
Скорость		v		Угловая скорость			ω
Ускорение		a		Угловое ускорение			ε
Импульс		mv		Момент импульса			Iω
Уравнение динамики	ma = F			Уравнение динамики		Iε = M
Кинетическая энергия		mv 2		Кинетическая энергия			Iω 2
	2					2

CИЛОВОЕ ПОЛЕ КОНСЕРВАТИВНЫХ СИЛ Материальная точка, оказавшаяся в силовом поле, обладает в каждой

точке поля потенциальной энергией и подвергается действию консервативной силы со стороны поля, «толкающей» эту материальную точку в сторону уменьшения энергии – принцип минимума энергии. Причем работа по пере-

мещению материальной точки осуществляется за счет потенциальной энергии Ep.

Сила называется консервативной, если работа этой силы не зависит от траектории.

2	Так работа силы	r	на пути 1 – a – 2 равна работе
		Fкнс
a
	этой силы на пути 1 – b – 2:
		r	r	r	r
		∫Fкнс dr =		∫Fкнс dr		.
	1−a −2			1−b −2

b

1

Из определения консервативной силы следует, что работа консервативной силы по любой замкнутой траектории равна нулю.

rr

∫Fкнс dr = 0 .

l

Докажем это:

r	r	r	r	r	r	r	r	r
∫Fкнс dr =		∫Fкнс dr +		∫Fкнс dr		= ∫Fкнс −	∫Fкнс dr = 0.
l		1−a −2		2−b−1		1−a −2	1−b−2
Такой интеграл от вектора по замкнутой траектории называется цирку-
ляцией этого вектора. Здесь это циркуляция вектора силы.
Консервативными являются гравитационная, кулоновская силы и силы
абсолютной упругости.
Потенциальная энергия как функция координат E p								= f (x, y, z ) – пред-
ставляет собой потенциальное числовое поле.
Вектор силы как функция координат
			r	r		r
			F = Fx i + Fy j + Fz k

– векторное поле.

Поскольку работа консервативной силы совершается за счет потенциальной энергии, имеем

δA = −dE p .

Дифференциал потенциальной энергии имеет вид:

dE		=	∂E p	dx +	∂E p	dy +	∂E p	dz .
	p
			∂x		∂y		∂z

Сравнив его с выражением для элементарной работы

δA = Fx dx + Fy dy + Fz dz ,

получим формулы связи консервативной силы с потенциальной энергией в дифференциальном виде:

		= −			dE p
Fx								,
					dx
					dE	p				r	.
Fy		= −							,	F = − gradE p
					dy
			dE p
F		= −						,
	z				dz

где gradE p – вектор, называемый градиентом потенциальной энергии,

и в интегральном виде:

2	r	r
∫F dr			= E p1 − E p 2	.
1

Вслучае так называемого центрального поля сил консервативная сила

ипотенциальная энергия зависят только от радиуса, т.е. от расстояния от центра поля. В этом случае

F = − dE p , E p = −∫F dr + const . dr

МЕХАНИЧЕСКАЯ ЭНЕРГИЯ Кинетическая и потенциальная энергии вместе составляют механиче-

скую энергию тела.

Работа консервативных сил не приводит к изменению механической энергии, «сохраняют» ее. Поэтому эти силы так и называются.

ДИССИПАТИВНЫЕ СИЛЫ Диссипативными называются силы, в результате работы которых меха-

ническая энергия тел превращаются в их внутреннюю (тепловую) энергию. Диссипативными являются все силы трения.

Эти силы всегда направлены прямо противо-

vположно вектору скорости. Их работа всегда зави-

Fтр	сит от траектории движения тела.
		r
			r		.
		δAдсп = F dr		= −F dr

ЗАКОН СОХРАНЕНИЯ И ПРЕВРАЩЕНИЯ ЭНЕРГИИ Среди сил, действующих на тело, есть внутренние консервативные,

внутренние диссипативные и внешние силы. Работа A всех сил будет равна сумме работы Aвнтр.кнс внутренних консервативных сил, работы Aвнтр.дсп внутренних диссипативных сил и работы Aвнш внешних сил. Работа всех сил равна изменению кинетической энергии тела. Работа внутренних консервативных сил равна со знаком «–» изменению его потенциальной энергии. Таким образом, получим:

Ek 2 − Ek1 = E p1 − E p 2 + Aвнтр.дсп + Aвнш

или

(Ek 2 − Ek1 )+ (E p 2 − E p1 ) = Aвнтр.дсп + Aвнш –

закон сохранения и превращения энергии: изменение механической энер-

гии системы тел равно сумме работ внутренних диссипативных и внеш- них сил.

Работа диссипативных сил отрицательна и всегда приводит к уменьшению механической энергии путем ее превращения во внутрен- нюю.

Механическая энергия замкнутой консервативной системы тел не изменяется.

Ek1 + E p1 = Ek 2 + E p 2 .

ЗАКОНЫ СОХРАНЕНИЯ И СТРУКТУРА ПРОСТРАНСТВА – ВРЕМЕНИ

Все основные законы сохранения связаны со свойствами простран- ства и времени: