lek2

ЧАСТЬ 2. ОСНОВЫ КЛАССИЧЕСКОЙ МЕХАНИКИ

Механика – часть физики, изучающая движение и взаимодействие физических тел в пространстве и времени. При этом физика имеет дело не с реальными телами: автомобилями, поездами, пушками, снарядами и т.д., а с физическими моделями, заменяющими эти реальные тела.

Кинематика – часть механики, изучающая характеристики движения: скорость и ускорение физических тел. Динамика – часть механики, изучающая взаимодействие физических тел как причину ускорения.

ПРОСТРАНСТВО И ВРЕМЯ В КЛАССИЧЕСКОЙ МЕХАНИКЕ В классической механике пространство считается абсолютным, то есть

не зависящим от наличия в нем материи. Пространство рассматривается как вместилище для материи. Пространство прямолинейно, трехмерно, бесконечно, безгранично, однородно (одинаково устроено в любой его точке) и изотропно (одинаково устроено по всем направлениям).

Время считается абсолютным, то есть не зависящим от пространства и процессов, происходящих с материей. Время бесконечно и однородно.

КИНЕМАТИКА МАТЕРИАЛЬНОЙ ТОЧКИ Если все точки физического тела движутся одинаково (тело при этом

не поворачивается), это физическое тело можно заменить моделью – материальной точкой.

Движение материальной точки рассматривается по отношению к некоторой системе отсчета – декартовой системе координат, связанной с какой-нибудь точкой пространства или телом отсчета (cм. рисунок).

Некоторая система отсчета К = {x, y, z}, связанная, например, с Землей, считается неподвижной и называется лабораторной. Любая другая система отсчета К′ = {x′, y′, z′}, движущаяся относительно системы К, называется подвижной.

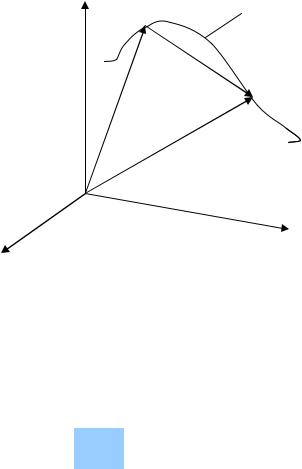
Вдоль осей координат направлены единичные векторы – орты: i –

вдоль оси x, j – вдоль оси y, k – вдоль оси z.

r

=

r

=

r

= 1.

i

j

k

Положение материальной точки в пространстве определяется ее координатами x, y, z в системе отсчета (измеряемыми в метрах) и радиусом – вектором r , проведенным из начала отсчета в данную точку. Координаты материальной точки являются и координатами (проекциями) радиуса – вектора. Координаты являются явными функциями от времени.

	r	r	r
	r	= x i + y j + z k , м.
Пусть в процессе движения материальная точка переместилась из точ-
ки 1 с радиусом – вектором	r	в точку 2 с радиусом – вектором			r	. При этом
	r1				r2
материальная точка совершила перемещение
		r	r	r
		r	= r2	− r1 .

zтраектория

1

r1			r
			2
			r2
0
x			y
r	r	, и r	обозначены без стрелок жирным шрифтом.
На рисунке векторы r1	, r2

Перемещение в единицу времени есть вектор скорости. Вектор мгно-

венной скорости определяется как производная от радиуса – вектора по времени:

r

dx r

dy r

dz r

r

r

r

dr

v

=

=

i +

j +

k = vx i + v y j + vz k , м/с.

dt

dt

dt

dt

Вектор скорости является явной функцией от времени. Модуль вектора скорости можно вычислить по формуле

	r
	v	= v 2		+ v 2	+ v 2	.
			x	y	z

Любое криволинейное движение можно представить в виде векторной суммы трех прямолинейных движений по осям x, y и z.

Материальная точка движется по некоторой линии – траектории. Век-

тор мгновенной скорости направлен по касательной к траектории. Дли-

на пройденной траектории называется пройденным путем S и измеряется в метрах (м). Пройденный путь является монотонно возрастающей функцией времени: S = f (t ).

Производная от пройденного пути по времени есть модуль мгно- венной скорости:

	r	=	dS	, м/с,
	v
			dt

где dS – дифференциал (бесконечно малое приращение) пройденного пути S, а dt– дифференциал времени t. Модуль мгновенной скорости является явной функцией от времени.

Чтобы вычислить пройденный путь, нужно проинтегрировать модуль мгновенной скорости по времени от 0 до t:

t r

S = ∫ v dt .

0

Для вычисления средней скорости нужно пройденный путь за время t разделить на это время:

vср = S .

t

Если движение происходит в плоскости, достаточно двух осей координат. Имеем x = f1 (t ), y = f 2 (t ). Исключив из обоих равенств время t, получим уравнение траектории y = f (x).

Так же для плоской траектории имеем vx

=

dx

и v y

=

dy

, откуда

dt

dt

vx

=

dx

dt

=

dx

.

v y dt dy dy

Если вектор скорости в процессе движения изменяется, то материальная точка движется с ускорением. Ускорение – это изменение скорости в единицу времени. Вектор мгновенного ускорения равен производной от вектора скорости по времени:

			r		r	r
	r		dv				2
	a	=			= a x i + a y j + a z k , м/с .
			dt

Модуль вектора ускорения можно вычислить по формуле

	r
	a	= a 2		+ a 2	+ a 2	.
			x	y	z

Вектор v может изменяться по величине и по направлению. Если вектор скорости по величине не меняется, то движение равномерное, если меняется – то неравномерное. Если вектор скорости по направлению не меняется, то движение прямолинейное, если меняется, то криволинейное. Таким образом, имеют место четыре вида движений:

1)прямолинейное и равномерное, если v = const;

2)прямолинейное и неравномерное;

3)криволинейное и равномерное;

4)криволинейное и неравномерное.

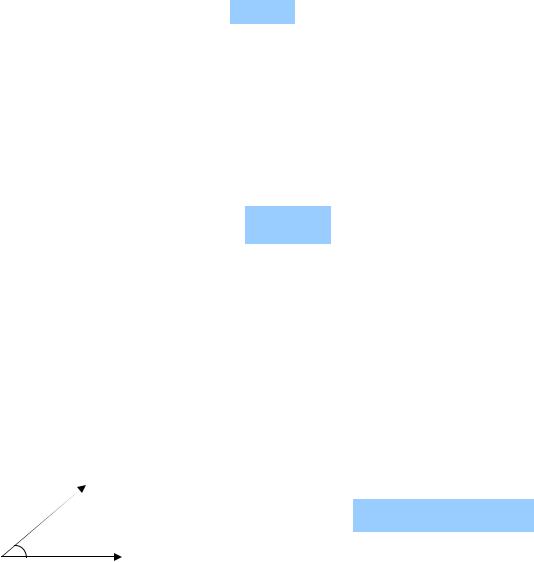
Если вектор a = const, то движение материальной точки является равноускоренным. Можно доказать, что траекторией равноускоренного движения является прямая, если вектор v параллелен вектору a , или парабола, ес-

ли вектор v не параллелен вектору a .
На этом рисунке векторы v	и a	обозначены
r	r

vжирным шрифтом.

	Если вектор v	параллелен вектору a , то движе-
	r	r
	ние прямолинейное.
	a
α	Если угол α острый, то движение криволиней-

ное и ускоренное.

Если угол α тупой, то движение криволинейное и замедленное

Различают две основные задачи механики: прямую и обратную.

1.Если известен закон движения, т.е. известны в явном виде зависимости координат материальной точки от времени, то можно путем взятия производных вычислить проекции векторов скорости и ускорения – прямая задача.

2.Если известны начальные координаты материальной точки, вектор начальной скорости, и зависимость вектора ускорения от времени, то можно путем интегрирования по времени получить закон движения, т.е. зависимости координат от времени – обратная задача:

	r	r	t	r
	v	= v0	+ ∫a		dt	,
			0
	r	r	t	r
	r	= r0	+ ∫v		dt	.
			0

ДИНАМИКА МАТЕРИАЛЬНОЙ ТОЧКИ Причиной изменения скорости тела является действие силы на это те-

ло. Если на материальную точку никакие силы не действуют, то она движется относительно Вселенной прямолинейно и равномерно или покоится. Связанная с такой точкой система отсчета называется инерциальной системой отсчета. Все инерциальные системы отсчета движутся относительно друг друга и относительно Вселенной прямолинейно и равномерно. Существование инерциальных систем отсчета утверждается первым законом Ньютона.

В природе существует только взаимодействие между телами. На каждую силу действия со стороны одного из взаимодействующих тел на другое следует ответ (реакция) – сила противодействия со стороны этого другого тела на первое. Причем сила – это вектор.

Третий закон Ньютона утверждает, что сила действия и сила про- тиводействия всегда направлены по одной прямой навстречу друг другу и равны по величине:

F1−2 = − F2−1 .

Каждое физическое тело обладает массой, которая позволяет ему сохранять свое механическое состояние, т.е. двигаться с постоянной скоростью или покоиться. Масса тела – мера его инертности. Чем больше масса тела, тем меньше ускорение при одном и том же воздействии на это тело:

a1

=

m2

, m a = m

при

r

=

r

,

a

F

F

2

a2

m1

1

1

2

1

2

откуда следует, что вектор силы можно определить как произведение массы тела на вектор его ускорения:

	r	r	,	кг м	.
	F	= m a
				с2

Второй закон Ньютона утверждает, что в инерциальной системе отсчета ускорение тела создается совместным действием всех остальных тел на данное тело. Причем все реальные силы, источником каждой из которых должно быть конкретное тело, складываются как векторы, от- куда

	r	r
		= ∑Fi	.
	m a
		i

Эта формула является аналитическим выражением второго закона Ньютона.

РАБОТА И МОЩНОСТЬ

r

Элементарной работой силы F называется скалярное произведе- ние этого вектора силы на вектор элементарного перемещения:

F

r	r		r		r	cosα	.
δA = F dr		=	F		dr

α

dr

δA – бесконечно малая величина, но не дифференциал, поэтому использован символ δ. Как будет показано, работа может зависеть от траектории, в то время как дифференциал никогда не зависит от траектории.

Как известно, скалярное произведение двух векторов равно сумме произведений одноименных координат этих векторов, откуда

δA = Fx dx + Fy dy + Fz dz .

Чтобы вычислить работу по перемещению материальной точки из точки 1 траектории в точку 2, нужно взять интеграл

2	r	r	, Дж.
A = ∫F dr
1

Работа, совершенная в единицу времени называется мощностью, которая измеряется в Ваттах (Вт):

P = A , Дж/с = Вт.

t

Для вычисления мгновенной мощности нужно взять производную:

		δA		r	r r
				F dr		.
	P =		=		= F v
		dt		dt

КИНЕТИЧЕСКАЯ ЭНЕРГИЯ Согласно второму закону Ньютона, векторная сумма всех сил сообщает

телу ускорение, и скорость тела изменяется. Покажем, что работа всех сил,

действующих на материальную точку, равна изменению ее кинетиче- ской энергии.

2	r r	2			2	r		2			mv 2		mv 2
			r	r		dv	r		r r
A = ∫∑Fi dr		= ∫ma		dr	= ∫m		dr	= ∫m v dv		=	2	−	1	,
						dt					2		2
1	i	1			1			1

где Ek = mv 2 – кинетическая энергия материальной точки.

2

ИМПУЛЬС МАТЕРИАЛЬНОЙ ТОЧКИ

Импульсом материальной точки называется векторная физиче- ская величина, равная произведению массы этой материальной точки на вектор ее скорости:

p = m v .

Покажем, что производная от вектора импульса материальной точки по времени равна векторной сумме сил, действующих на эту материальную точку:

	r		r
	dp	= m	dv
	dt		dt

r	r
= m a	= ∑Fi .
	i

Это уравнение также является уравнением второго законы Ньютона.

Чтобы найти изменение импульса, нужно проинтегрировать векторную сумму всех сил по времени:

r t ∑ r

p = ∫ Fi dt .

0i

Итак, чтобы изменить импульс материальной точки, нужно подей- ствовать на нее некоторой силой в течение длительного времени.

ЗАКОН СОХРАНЕНИЯ ИМПУЛЬСА Взаимодействующие между собой тела – материальные точки – состав-

ляют систему. Импульс системы материальных точек – это векторная сумма

импульсов всех материальных точек, составляющих систему:	r	r
	p = ∑mi vi .

i

Производная от вектора импульса системы материальных точек по времени равна векторной сумме сил, действующих между материальными точками, составляющими систему – внутренних сил, и сил, действующих на материальные точки, составляющие систему, со стороны тел, не входящих в систему, – внешних сил. Но векторная сумма всех внутренних сил как сил действия и противодействия по третьему закону Ньютона равна нулевому вектору. Итак, получим

	r	r	r	r
	dp
		= ∑F	внтр + ∑Fвнш = ∑Fвнш		,
	dt

откуда изменение импульса системы будет равно интегралу от векторной суммы всех внешних сил по времени:

r t ∑ r

p = ∫ Fвнш dt ,

0

то есть изменить импульс системы материальных точек могут только внешние силы, действующие в течение некоторого промежутка времени.

Таким образом, если внешние силы на систему не действуют, а такая система материальных точек называется замкнутой, то импульс такой системы не изменяется, то есть сохраняется.

Мы получили закон сохранения импульса: импульс замкнутой систе-

мы не изменятся, какие бы взаимодействия и превращения ни происхо- дили бы внутри этой замкнутой системы.

Если внешние силы компенсируют друг друга, то импульс системы также не изменяется.

Если внешние силы на систему все же действуют и не компенсируют друг друга, то в ходе процессов внутри системы, происходящих в течение очень малого промежутка времени, как это бывает при ударе тел или при взрыве, импульс системы также можно считать неизменным, т.е. применить к этой системе закон сохранения импульса.

При абсолютно неупругом ударе двух шаров эти шары как бы слипаются, образовав одно тело. В этом случае уравнение закона сохранения импульса имеет следующий вид:

m1v1 ± m2 v2 = (m1 + m2 ) v ,

при этом знак «+» ставится, если шары до удара двигались навстречу друг другу, и знак «–», если в одну сторону.

АБСОЛЮТНО ТВЕРДОЕ ТЕЛО. УГЛОВАЯ СКОРОСТЬ. УГЛОВОЕ УСКОРЕНИЕ

Если физическое тело поворачивается, и это вращение принципиально важно для конкретной задачи, то это тело нельзя считать материальной точкой. В этом случае используется другая модель – абсолютно твердое тело. В дальнейшем слово «абсолютно» будем опускать.

Пусть некоторое твердое тело вращается вокруг оси 0z с угловой скоростью ω. С помощью правила буравчика определяют вектор ϕ угла поворо-

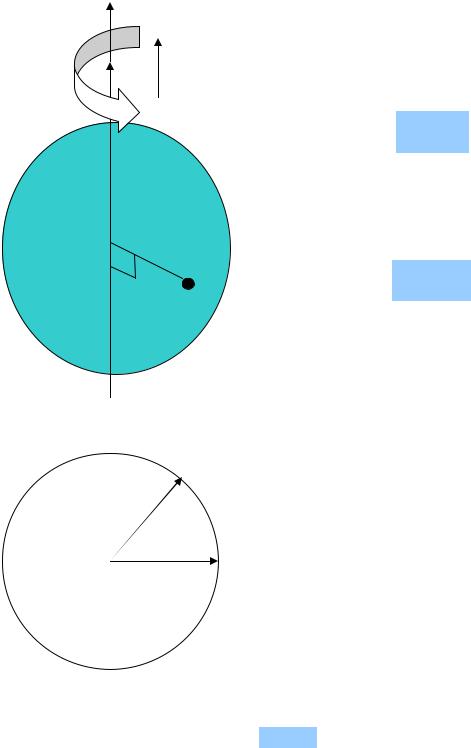
та этого тела (на рисунке вектор ϕ обозначен жирным шрифтом) Этот вектор параллелен оси вращения. Если он направлен на нас, то тело вращается против часовой стрелки, как это и показано на рисунке. Величина этого вектора измеряется в радианах, т.е. в безразмерных единицах.

φ

	ω	Вектор угловой скорости равен
z		производной от вектора угла пово-
		рота тела по времени:
					r	1
			r	=	dϕ				.
			ω			,
					dt		c

0

анах, на радиус r:

Вектор углового ускорения ра- вен производной от вектора угловой скорости тела по времени:

r			r	1
	r	=	dϕ				.
	ε			,
dm			dt		c 2

			Ели тело вращается вокруг оси
			0z, каждая точка этого тела движется
r		S	по окружности радиуса r, перпендику-
	φ
			лярной этой оси, и за некоторое время
			t описывает дугу, длина которой S
			равна произведению угла поворота те-
			ла φ, выраженного обязательно в ради-

S = ϕ r .