lek6

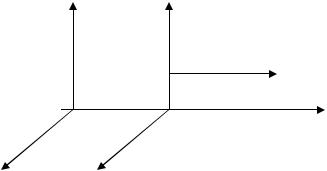
ЧАСТЬ 6.

ОСНОВЫ СПЕЦИАЛЬНОЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ

ПРЕОБРАЗОВАНИЯ ГАЛИЛЕЯ И СКОРОСТЬ СВЕТА

Пусть некоторая система отсчета К = {x, y, z} считается неподвижной, а система отсчета К′ = {x′, y′, z′} движется относительно системы К с постоянной скоростью v0. Оси координат обеих этих инерциальных систем отсчета расположим так, как показано на рисунке ниже.

	y	y′		Оси 0x и 0x′ совпадают и
				расположены параллельно
			v0	вектору скорости v0. Ось 0y
		v0t		параллельна оси 0y′, а ось
	0	0′	x, x′	0z параллельна оси 0z′. В
				момент времени t0 = 0 обе
z	z′			системы совместились.

Спустя промежуток времени t система К′ переместилась на расстояние v0t. Некоторая точка в пространстве имеет в системе К координаты (x, y, z),

а в системе К′ – координаты (x′, y′, z′). Переход от координат точки в системе К′ к ее координатам в системе К имеет вид:

x = x′ + v0 t,

y = y′,

z = z′.

Эта система уравнений называется преобразованиями Галилея. Преобразования Галилея соответствуют представлениям классической механики.

Пусть в момент времени t0 = 0, когда обе системы отсчета были совмещены, в точке х = х′ = 0 произошла вспышка света. Спустя промежуток времени t луч света вдоль оси 0х′ достиг некоторой точки с координатой х′ = сt. Координата этой же точки в системе К согласно преобразованиям Галилея будет равна

x = ct + v0 t .

Получается, что в системе К луч свете достиг этой точки со скоростью

x = c + v0 . t

Таким образом, скорость света оказалась зависящей от скорости наблюдателя, и по отношению к разным системам отсчета скорость света оказалась различной.

Все эксперименты, поставленные с целью обнаружения зависимости скорости света в вакууме от системы отсчета, дали отрицательный результат. С другой стороны, в электромагнитной теории, скорость света в вакууме представляет собой физическую константу, а не скорость какого-то материального объекта. Обнаружилось противоречие между классической механикой и электромагнетизмом. Это противоречие было устранено Альбертом Эйнштейном.

ПОСТУЛАТЫ СПЕЦИАЛЬНОЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ Эйнштейн изменил классические представления о независимых друг от

друга пространстве и времени таким образом, чтобы скорость света в вакууме была одинаковой для всех наблюдателей, а все законы физики имели одну и ту же форму для всех инерциальных систем отсчета. Для этого пространство и время нужно рассматривать как единый пространственно – временной континуум – четырехмерное пространство – время. Время должно зависеть от пространства и в разных системах отсчета идти по-разному.

В основе специальной теории относительности (СТО) лежат два посту-

лата:

1.Все законы природы одинаковы во всех инерциальных системах отсчета, и абсолютное движение обнаружить невозможно – принцип от-

носительности.

2.Скорость света в вакууме одинакова во всех инерциальных сис- темах отсчета и не зависит от движения источника или наблюдателя –

принцип постоянства скорости света.

ПРЕОБРАЗОВАНИЯ ЛОРЕНЦА В представлениях о четырехмерном пространстве – времени любая

точка будет иметь четыре координаты. В качестве четвертой координаты возьмем ct.

Теперь переход от координат точки в системе K ′ = {x′, y′, z′, ct ′} к ее ко-

ординатам в системе K = {x, y, z, ct} должен удовлетворять обоим постулатам.

Согласно принципу относительности переходы от системы K ′ к системе K и наоборот от системы K к системе K ′ должны быть выражены одинаковыми уравнениями. Кроме того, эти уравнения должны удовлетворять и принципу постоянства скорости света. Этим условиям соответствуют преобразования Лоренца:

x = γx′ + γβct ′, (1)

y = y′,z = z ′,

ct = γβx′ + γct ′(2)

	x′ = γx − γβct, (3)
и	y′ = y,
	z′ = z,
	ct ′ = −γβx + γct.(4)

В этих уравнениях

γ =	1			, β =	v0	.
	1 − β 2				c

Видно, что эти системы устроены одинаково. Знак «минус» при членах с β в системе справа учитывает направление скорости v0. Остается доказать, что эти преобразования удовлетворяют и принципу постоянства скорости света, то есть доказать, что из условия x′ = ct ′ следует x = ct . Для этого разделим уравнение (1) на уравнение (2):

						x′
		γ (x′ + βct ′)			ct ′		+ β
x	=			=	ct ′				=	1 + β	= 1,
					βx′
ct γ (βx′ + ct ′)										β + 1
					ct ′			+ 1
					ct ′

что и требовалось доказать. Разделив уравнение (3) на уравнение (4), можно показать, что из условия x = ct следует x′ = ct ′ .

Именно Эйнштейн придал преобразованиям Лоренца новый физический смысл. В соответствии с этими преобразованиями изменяются не размеры физических тел, как это считали раньше, а само пространство – время.

ОТНОСИТЕЛЬНОСТЬ ОДНОВРЕМЕННОСТИ

Если в двух разных точках на оси 0х два события произошли одно- временно, то по отношению ко всем наблюдателям, движущимся отно- сительно оси 0х, эти же события произошли не одновременно. Причиной этому является постоянство скорости света относительно любых инерциальных систем отсчета.

	Для доказательства		отно-
	сительности	одновременности
A	используем	мысленный	экспе-
	B

римент Эйнштейна, схема которого изображена на рисунке сле-

Kва.

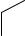
L

M

Пусть в точках A и B произошли вспышки света. Пусть потом в некоторый момент времени все три наблюдателя оказались точно напротив середины отрезка AB. Пусть в этот же момент времени свет от точек A и B одновременно достигнет середины отрезка. С этими условиями согласятся все три наблюдателя.

Теперь встает вопрос о том, когда произошли вспышки света в точках A и B. По этому вопросу наблюдатели не договорятся.

Примем точку зрения наблюдателя К. Вспышки света дошли до середины отрезка AB одновременно. При этом свет с одинаковой скоростью прошел одинаковые расстояния, а значит, затратил одинаковые промежутки времени. Следовательно, вспышки света в точках A и B произошли одновре-

менно.

Теперь примем точку зрения наблюдателя L. И для него вспышки света дошли до середины отрезка AB одновременно. Но, когда произошли эти вспышки, точка В находилась дальше от наблюдателя L, чем точка А. Значит свет, пришедший из точки В затратил больше времени. Следовательно, вспышка света в точке В произошла раньше, чем в точке А. Итак, вспышки света в точках A и B произошли не одновременно.

С точки зрения наблюдателя М вспышка света произошла раньше в точке А. Следовательно и для него вспышки света в точках A и B произошли

не одновременно.

РЕЛЯТИВИСТСКОЕ СОКРАЩЕНИЕ ПРОСТРАНСТВА Законы, открытые Эйнштейном, получили название релятивистских.

Одним из релятивистских эффектов является релятивистское сокращение пространства.

А

l0

В

v

x ′, x

Пусть ось 0x′ проходит через две точки А и В. Пусть отрезок АВ покоится в системе отсчета К′ и движется со скоростью v относительно системы К вдоль оси 0х.

Будем считать, что расстояние между точками А и В равно длине отрезка АВ. Длина этого отрезка будет равна модулю разности координат концов отрезка, но при обязательном условии: координаты начала и конца от-

резка должны быть измерены одновременно.

	Введем следующие обозначения:
l0 = xB	− x A	при t A		= t B	– длина отрезка в системе отсчета К′,
′	′		′	′
l = xB − xA		при t A = t B			– длина отрезка в системе отсчета К.
Но если t A			= t B , то t A ≠ t B и наоборот. Следовательно, расстояния между точ-
		′	′

ками А и В в разных системах отсчета различны.

Получим формулу связи между этими расстояниями. Разность координат точек А и В в системе 0х′ равна l0. Разность координат точек А и В в системе 0х найдем с помощью уравнения (1) из преобразований Лоренца:

x

B

− x

A

= γ (x′

− x′

)+ γβ (ct ′

− ct ′ ).

B

A

B

A

С помощью уравнения (4) получим:

ct ′

− ct ′

= −γβ (x

B

− x

A

)+ γ (ct

B

− ct

A

).

B

A

Если последняя разность равна нулю, то есть t A = t B , то xB − x A = l . Тогда по-

лучим:

l = γl

0

− γ 2 β 2 l .

Далее

l = l0

γ

= l0

γ

=

l0

= l

1 −

v 2

, поскольку

1

+ β 2 = 1 .

1

+ γ 2 β 2

γ 2

0

c 2

γ 2

γ

Итак, мы получили формулу релятивистского сокращения пространст-

ва:

	l = l		1 −		v 2	.
		0			c 2

Согласно этой формуле наблюдатель, движущийся вдоль отрезка, собственная длина которого равна l0 , получит при измерении длины этого отрезка величину l, меньшую, чем l0. Таким образом, для движущегося наблюдателя пространство вдоль направления его движения сокращается.

РЕЛЯТИВИСТСКОЕ ЗАМЕДЛЕНИЕ ВРЕМЕНИ Пусть в некоторой точке пространства одно за другим произошли два

события. И пусть в системе отсчета К′, относительно которой эта точка поко-

ится, промежуток времени между этими событиями будет равен t	0	= t ′	− t ′ .
		2	1

Промежуток времени t между этими же событиями в системе К получим с помощью уравнения (2) из преобразований Лоренца:

c(t	2	− t	1	) = γc(t ′	− t ′ ).
				2	1

Итак, мы получили формулу релятивистского замедления времени:

t =		t	0			.
	1 −			v 2
				c 2

Согласно этой формуле наблюдатель, движущийся относительно системы отсчета, в которой происходят некоторые события с промежутком t0, получит при измерении промежутка времени между этими событиями величину t, большую, чем t0. Таким образом, для движущегося наблюдателя вре-

мя замедляется.

РЕЛЯТИВИСТСКИЙ ИМПУЛЬС И РЕЛЯТИВИСТСКАЯ ЭНЕРГИЯ Если преобразования Лоренца продифференцировать по собственному

времени некоторой движущейся частицы с учетом замедления времени, то мы получим новые, релятивистские выражения для импульса и полной энергии этой частицы, удовлетворяющие соответствующим законам сохранения:

r r mv

p = ,

1 −

v 2

c 2

mc 2

E = ,

1 −

v 2

c 2

где v – скорость частицы относительно данной системы отсчета, а m – ее масса покоя. Поскольку скорость движения относительна, импульс и энергия частицы зависят от системы отсчета.

Если частица покоится в некоторой системе отсчета, то ее энергия в этой системе будет равна величине

E0 = mc 2 ,

называемой энергией покоя частицы. Поэтому энергия Е называется полной, так как включает в себя и энергию покоя, и энергию движения.

Исключив скорость из выражений для импульса и полной энергии, получим формулу связи массы покоя частицы с ее релятивистскими импульсом и полной энергией:

E 2 = p 2 c 2 + m 2 c 4 .

Импульс и полная энергия частицы зависят от системы отсчета, а выражение

E 2 − p 2 c 2 = const ,

поскольку масса покоя частицы неизменна.

ИНТЕРВАЛ И ЧЕТЫРЕХВЕКТОР Как мы уже видели, при переходе от одной системы отсчета к другой

обычное трехмерное пространство и время сами по себе изменяются, но рас-

стояние между двумя точками в четырехмерном пространстве – времени остается неизменным. Это расстояние называют интервалом s. Квадрат интервала обычно записывают так:

s 2 = c 2 t 2 − (x 2 + y 2 + z 2 ).

Постоянство интервала

c 2 t 2 − (x 2 + y 2 + z 2 )= const ,

то есть его независимость от выбора системы отсчета, физики называют инвариантностью. Последнему равенству соответствует и ранее полученное равенство

E 2 − p 2 c 2 = const ,

в котором трем координатам x, y, z соответствуют три проекции вектора им-

пульса px, py, pz, а координате ct соответствует выражение					E	.
					c
Таким образом, в четырехмерном пространстве – времени полная энер-
гия и импульс составляют четырехвектор:
		E		.
	p x , p y , p z ,
		c

Четырехвектор также инвариантен, то есть одинаков, по отношению к любой системе отсчета.

РЕЛЯТИВИСТСКАЯ КИНЕТИЧЕСКАЯ ЭНЕРГИЯ Любая массивная частица в каждой системе отсчета обладает энергией

покоя благодаря своей массе и энергией движения, то есть кинетической энергией. В сумме эти две энергии составляют полную энергию частицы. Следовательно, релятивистская кинетическая энергия частицы равна разности между полной ее энергией и энергией покоя этой частицы:

Ek = E − mc 2 .

Согласно принципу соответствия релятивистское выражение для кинетической энергии должно превратиться в классическое при условии v << c. Покажем это, воспользовавшись приближенным равенством

													v	2			2								v	2			при v << c.
											−										= 1		−
									1				2c		2										c	2
Имеем
		mc	2									mc		2													v		2				mc	2				v	2				mv	2
Ek =							− mc	2	=												1	−	1 −								=						1 − 1 +					=			,
																													2											2
				2												2																			2
	1 −		v								1 −			v													c					1 −		v				2c					2
			c	2										c		2																		c	2

что и требовалось доказать.

РЕЛЯТИВИСТСКИЙ ВТОРОЙ ЗАКОН НЬЮТОНА Уравнение второго закона Ньютона, записанное в виде

	r	r
	dp
		= ∑F	,
	dt

где p – вектор релятивистского импульса. Согласно этому уравнению им-

пульс частицы

r r	t	r
p = p0	+ ∫∑F dt
	0

по величине может расти хоть до бесконечности.

Но при этом скорость частицы, обладающей массой покоя, останется всегда меньше скорости света в вакууме. Покажем это.

Из определения релятивистского импульса

p =

mv

1 −

v 2

c 2

1

m 2

v 2

m 2 v 2

2

p 2

имеем

= 1 −

, потом

v

+

= 1 ,

откуда v = c

и оконча-

2

2

2

2

2

2 2

+ m c

c

p

c

p

p

тельно получим

v = c

1

.

2

1 +

mc

p

Последнее уравнение удобно для анализа поведения скорости в зависимости от импульса. При малых значениях импульса в знаменателе можно пренебречь единицей, и мы получим классическое соотношение

v = c	p 2	=	p	,
	m 2 c 2
			m

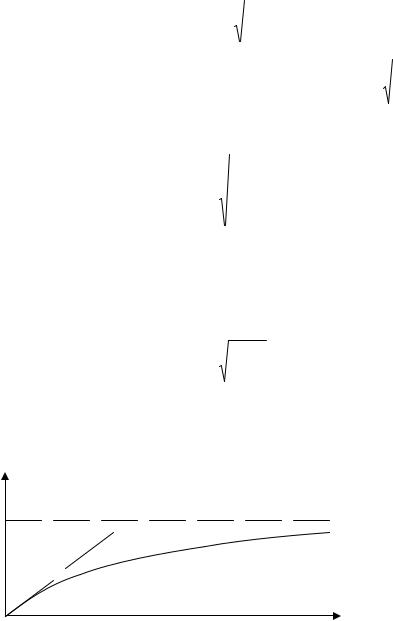
а при очень больших значениях импульса получим v → с, но все равно v < с. График зависимости скорости от импульса изображен ниже на рисунке.

v c

0

p

ПРИМЕР ПРИМЕНЕНИЯ РЕЛЯТИВИСТСКОГО ВТОРОГО ЗАКОНА НЬЮТОНА

Дальше идет необязательный материал, предназначенный для любо-

знательных студентов.