
- •II. Случайные величины и их распределения
- •2.1. Случайная величина
- •2.2. Дискретные случайные величины
- •2.3. Непрерывные случайные величины
- •2.4. Преобразование случайных величин
- •2.5. Математическое ожидание
- •2.6. Дисперсия случайной величины
- •2.7. Моменты случайных величин. Другие числовые характеристики случайных величин
- •2.8. Характеристические функции
- •2.9. Производящие функции
- •Контрольные вопросы
2.2. Дискретные случайные величины
Из теории меры
известно, что любая неубывающая функция
F(x) может быть представлена в виде суммы
трех функций: абсолютно непрерывной
функции
![]() ,
ступенчатой функции
,
ступенчатой функции![]() и сингулярной функции
и сингулярной функции![]() (непрерывной функции, множество точек
роста которой имеет лебегову меру нуль).
Следовательно,
(непрерывной функции, множество точек
роста которой имеет лебегову меру нуль).
Следовательно,![]() .
В реальных задачах теории вероятностей
сингулярная компонента почти не
встречается, она представляет собой
математическую абстракцию, потому будем
полагать
.
В реальных задачах теории вероятностей
сингулярная компонента почти не
встречается, она представляет собой
математическую абстракцию, потому будем
полагать![]() .
Остановимся на двух крайних случаях:
.
Остановимся на двух крайних случаях:![]() и
и![]() .
.
В первом случае
F(x) – ступенчатая функция, имеющая в
точках
![]() cкачки. Величина скачков в этих точках
равна соответственно
cкачки. Величина скачков в этих точках
равна соответственно![]() то есть
то есть![]()
![]()
![]() Случайная величина ξ, для которой F(x)
является функцией распределения,
называется в этом случаедискретной
случайной величиной. Числа
Случайная величина ξ, для которой F(x)
является функцией распределения,
называется в этом случаедискретной
случайной величиной. Числа
![]() –
это те значения, которые случайная
величина принимает при различных
–
это те значения, которые случайная
величина принимает при различных![]() ,
а числа
,
а числа![]() – это вероятности, с которыми сл. величина
принимает соответствующие значения
– это вероятности, с которыми сл. величина
принимает соответствующие значения![]()
Определение
дискретной случайной величины можно
дать и
не опираясь на ее функцию
распределения. Случайная величина ξ
называется дискретной,
если она каждому элементарному исходу
ставит в соответствие одно
число из конечного или счетного множества
чисел
![]() ,
причем вероятность события
,
причем вероятность события![]()
![]()
Обычно дискретные
случайные величины задаются рядом
распределения.
Это может быть таблица из двух строк,
в первой, верхней, строке перечислены
все возможные значения случайной
величины
![]() ,
а во второй строке проставлены вероятности
,
а во второй строке проставлены вероятности![]()
|
Х |
x1 |
x2 |
x3 |
… |
xk |
… |
xn |
… |
|
P |
р1 |
р2 |
р3 |
… |
рk |
… |
рn |
… |
Очевидны ограничения
на числа
![]() :
:
1)
![]()
![]() 0;
2)
0;
2)![]() (2.3)
(2.3)
Часто вместо
таблицы просто указывают для сл. величины
все множество ее значений
![]() ,
k = 1, 2,… , и приводят формулу, по которой
можно вычислять вероятности событий
,
k = 1, 2,… , и приводят формулу, по которой
можно вычислять вероятности событий![]() для
всех
для
всех![]()
![]() .
Такой способ задания дискретной сл.
величины также называют рядом
распределения сл. величины.
.
Такой способ задания дискретной сл.
величины также называют рядом
распределения сл. величины.
Иначе говоря, рядом
распределения сл. величины называют
соответствие
![]()
Если при описании случайной величины ξ применяют какую-нибудь другую ее характеристику вместо функции распределения и при этом по этой характеристике возможно однозначно восстановить функцию распределения, то такая характеристика называется законом распределения случайной величины ξ или просто распределением случайной величины. Ряд распределения – это один из законов распределения случайных величин. В разделе 1.11 мы уже использовали термин «распределение» – называли гипергеометрическое распределение, распределение Бозе–Эйнштейна и т.д.
По ряду распределения можно однозначно восстановить функцию распределения:
![]() . (2.4)
. (2.4)
Пример 1.
Игрок выигрывает очко, если при подбрасывании монеты выпадает герб, и проигрывает очко в противном случае. Записать функцию распределения суммарного выигрыша игрока после двух бросаний монеты.
Решение.
Обозначим суммарный выигрыш игрока
после двух бросаний монеты через S;
возможные значения этой сл. величины
–2, 0 и 2, вероятности, с которыми эти
значения принимаются сл. величиной,
равны
![]() соответственно. Иначе говоря, распределение
сл. величины S выглядит следующим образом:
соответственно. Иначе говоря, распределение
сл. величины S выглядит следующим образом:
|
S |
–2 |
0 |
2 |
|
P |
0.25 |
0.5 |
0.25 |
Тогда
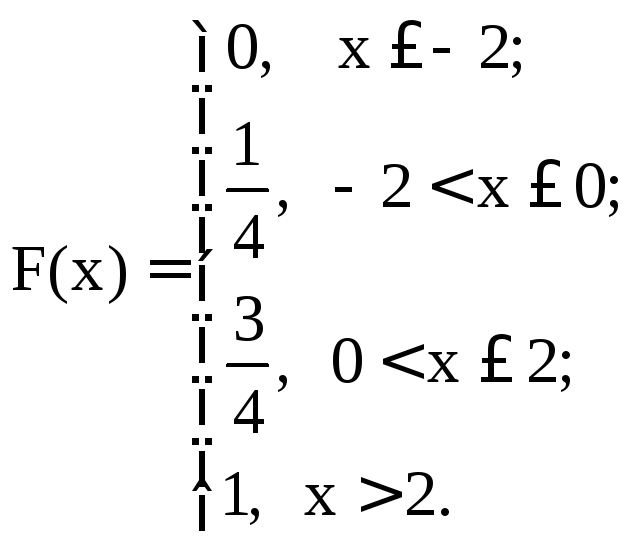
Пример 2. Техническое устройство состоит из трех узлов, работающих независимо друг от друга. Первый узел отказывает с вероятностью 0.1, второй и третий – с равными вероятностями 0.3. Устройство выходит из строя, если откажет первый узел или второй и третий вместе. Производится испытание до первого отказа, но не более четырех раз. Случайная величина Х – число произведенных испытаний. Требуется найти ряд распределения и функцию распределения сл. величины Х.
Решение. Как
следует из условия задачи, сл. величина
Х может принимать значения
![]() Вычислим вероятности
Вычислим вероятности![]() :
:![]() {отказал
первый узел или первый узел не отказал,
но отказали второй и третий узлы}
{отказал
первый узел или первый узел не отказал,
но отказали второй и третий узлы}![]()
![]() {прибор
не отказал в первом испытании, но отказал
во втором испытании}= 0.82 · 0.18 ≈ 0.15;
{прибор
не отказал в первом испытании, но отказал
во втором испытании}= 0.82 · 0.18 ≈ 0.15;![]() {прибор
не отказал в первых двух испытаниях, но
отказал в третьем испытании}=
{прибор
не отказал в первых двух испытаниях, но
отказал в третьем испытании}=![]()
![]() {прибор
не отказал в первых трех испытаниях}
{прибор
не отказал в первых трех испытаниях}![]()
Построим ряд распределения для сл. величины Х:
|
Х |
1 |
2 |
3 |
4 |
|
Р |
0.18 |
0.15 |
0.12 |
0.55 |
Найдем по формуле (2.4) функцию распределения
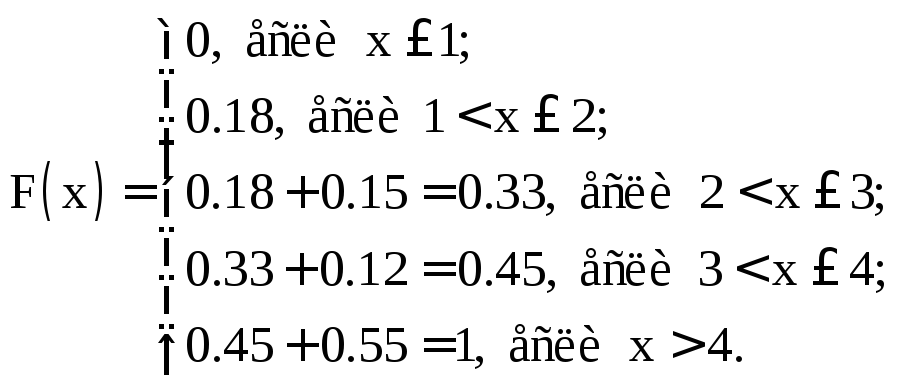
Рассмотрим некоторые дискретные случайные величины, с которыми будем работать в дальнейшем.
1. В качестве самой простой дискретной сл. величины рассмотрим случайную величину, принимающую единственное значение С. Очевидно, что это значение она принимает с вероятностью, равной единице. Тогда функция распределения сл. величины имеет вид:
![]()
2. Не менее простой дискретной сл. величиной является функция, называемая индикатором события А:
![]()
Рассмотрим сначала
один из примеров использования функции
![]() .
Пусть
.
Пусть![]() – дискретное вероятностное пространство
и ξ – некоторая сл. величина, принимающая
конечное множество значений
– дискретное вероятностное пространство
и ξ – некоторая сл. величина, принимающая
конечное множество значений![]() .
Если положить
.
Если положить![]() ,
то ξ можно представить в виде
,
то ξ можно представить в виде![]() ,
где события
,
где события![]() образуют разбиение пространства Ω –
они попарно не пересекаются и их сумма
равна Ω (то есть это полная группа
событий – см. также п.1.8).
образуют разбиение пространства Ω –
они попарно не пересекаются и их сумма
равна Ω (то есть это полная группа
событий – см. также п.1.8).
Ряд распределения
сл. величины
![]() имеет вид:
имеет вид:
|
|
0 |
1 |
|
Р |
|
|
Функция же распределения выглядит следующим образом:
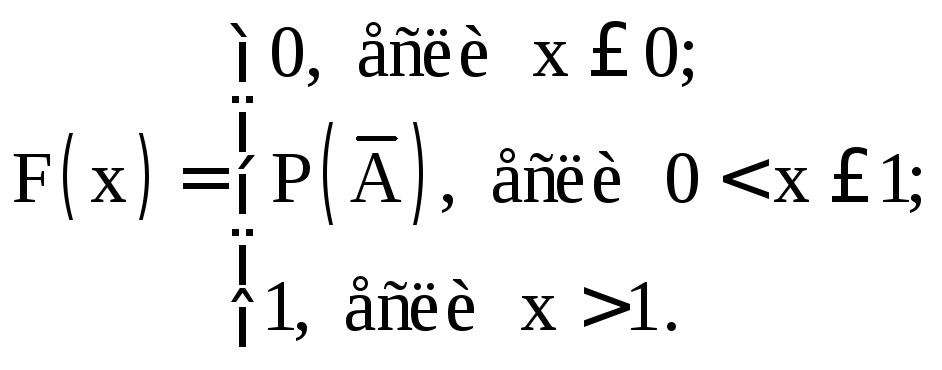
Пример 3.
Выпадение 6 очков при бросании игральной
кости назовем событием А. Тогда сл.
величина
![]() принимает значение 1, если выпадает 6
очков, и 0 – во всех остальных случаях.
Ее ряд распределения имеет вид:
принимает значение 1, если выпадает 6
очков, и 0 – во всех остальных случаях.
Ее ряд распределения имеет вид:
|
|
0 |
1 |
|
Р |
|
|
а функция
распределения имеет вид:
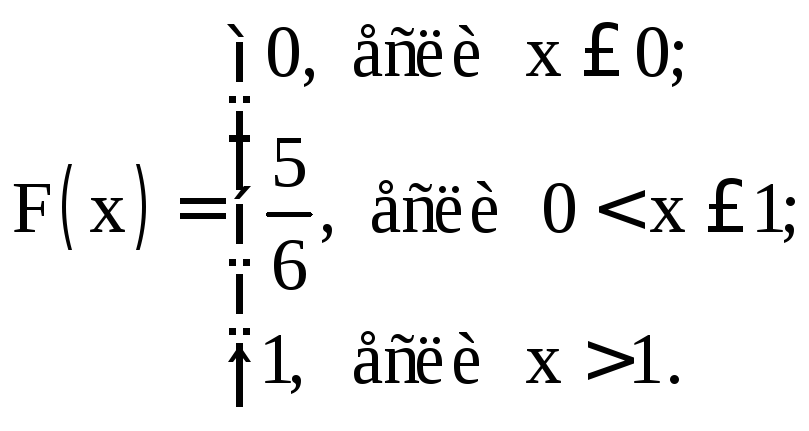
3. Распределение
Бернулли.
Случайная величина ξ имеет распределение
Бернулли с параметром
![]() ,
если ξ принимает только два значения 1
и 0 с вероятностями p и q = 1 – p соответственно.
,
если ξ принимает только два значения 1
и 0 с вероятностями p и q = 1 – p соответственно.
Ряд распределения этой сл. величины имеет вид
-
ξ
0
1
Р
q
p
а функция
распределения:
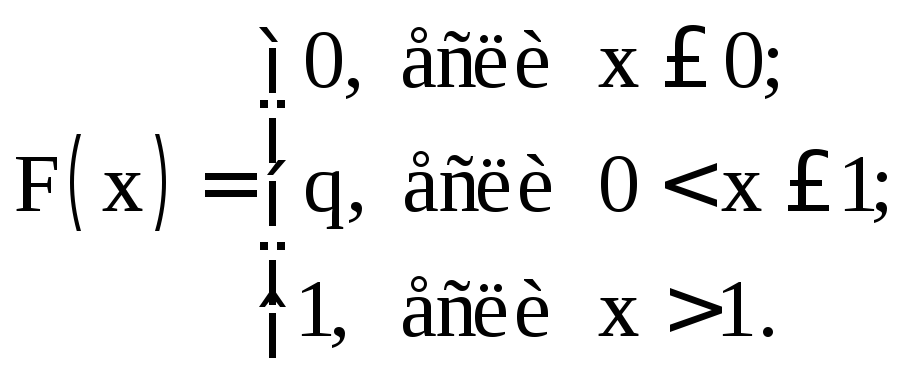 .
.
Условное обозначение
распределения Бернулли –
![]() .
Тот факт, что сл. величина ξ имеет
распределение Бернулли, обозначается
символом:
.
Тот факт, что сл. величина ξ имеет
распределение Бернулли, обозначается
символом:![]() или
или![]() .
.
4.
Биномиальное
распределение.
Обратимся к схеме Бернулли. Пусть в
этом эксперименте случайная величина
ξ – число успехов в серии из n независимых
испытаний. Тогда случайная величина ξ
может принимать значения
![]() .
Вероятность события
.
Вероятность события![]() ранее обозначалась нами как P(n, k), теперь
мы ее будем обозначать просто через
ранее обозначалась нами как P(n, k), теперь
мы ее будем обозначать просто через![]() .
Итак,
.
Итак,
![]() .
(2.5)
.
(2.5)
Формула (2.5)
определяет распределение дискретной
случайной величины, называемое
биномиальным
законом распределения с
параметрами распределения n, p. Для
краткости биномиальное распределение
обозначают символом В(n,p):
![]() имеет
место распределение (2.5).
имеет
место распределение (2.5).
На примере этого
закона распределения рассмотрим более
подробно, как по нему можно однозначно
восстановить функцию распределения
F(x). Поскольку
![]() ,
то для всех
,
то для всех![]() событие
событие![]() – невозможное, значит,
– невозможное, значит,![]() .
Если
.
Если![]() ,
то событие
,
то событие![]() состоит из тех и только тех элементарных
исходов ω, для которых
состоит из тех и только тех элементарных
исходов ω, для которых![]() ,
следовательно,
,
следовательно,![]() Если
Если![]() ,
то событие
,
то событие![]() состоит из тех элементарных исходов ω,
для которых
состоит из тех элементарных исходов ω,
для которых![]() или
или![]() ,
следовательно,
,
следовательно,![]() ,
и т. д.
,
и т. д.
Наконец, при
![]() событие
событие![]() достоверное событие и
достоверное событие и![]() Сведем результаты в одну формулу:
Сведем результаты в одну формулу:
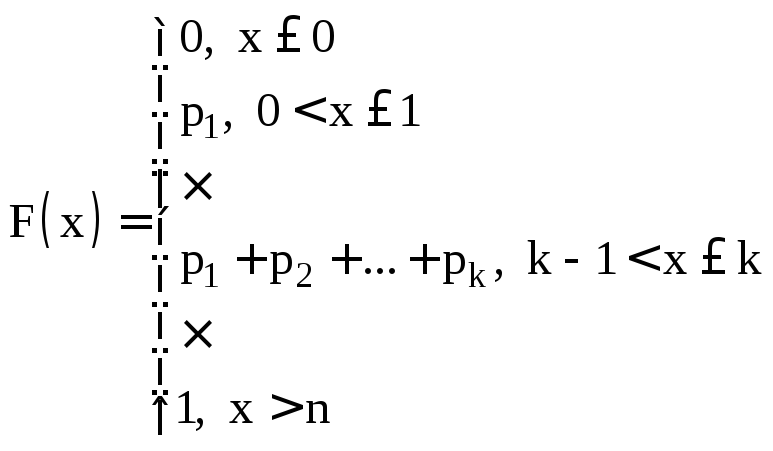
Очевидно, что описание случайной величины формулой (2.5) выглядит проще, чем описание ее с помощью функции распределения.
Пример 4.
На зачете студент получил четыре задачи.
Вероятность решить каждую задачу
правильно равна 0.4. Пусть ξ – число
правильно решенных задач. Описать закон
распределения сл. величины
![]() .
.
Решение. По
содержанию задачи случайная величина
ξ может быть описана биномиальным
законом распределения, решенная правильно
задача – успех. По формуле (2.5)
![]()
![]()
![]()
![]() ,
это ряд распределения сл. величины ξ.
Однако в реальной задаче, когда интерес
представляют значения вероятностей
,
это ряд распределения сл. величины ξ.
Однако в реальной задаче, когда интерес
представляют значения вероятностей![]() ,
ряд распределения удобно представить
таблицей:
,
ряд распределения удобно представить
таблицей:
|
|
0 |
1 |
2 |
3 |
4 |
|
P |
0.1296 |
0.3456 |
0.3456 |
0.1536 |
0.0256 |
5. Геометрическое
распределение.
Снова рассмотрим схему Бернулли. Пусть
ξ – число испытаний, которое необходимо
провести, прежде чем появится первый
успех. Предполагается, что в каждом
отдельном испытании успех достигается
с вероятностью р. Очевидно, что случайная
величина ξ может принимать счетное
множество значений k = 0, 1, 2, 3,…, n,…
Определим вероятность события
![]() .
Если
.
Если![]() ,
то в первых k испытаниях появилась
неудача, а в (k+1)-м испытании – успех. Как
дальше будут развиваться события при
изучении этой случайной величины, нас
не интересует. Элементарный исход
выглядит в этом случае так:
,
то в первых k испытаниях появилась
неудача, а в (k+1)-м испытании – успех. Как
дальше будут развиваться события при
изучении этой случайной величины, нас
не интересует. Элементарный исход
выглядит в этом случае так:![]() .Следовательно,
.Следовательно,
![]() Проверим равенство
Проверим равенство
![]() :
:![]() .
.
Итак,
![]() (2.6)
(2.6)
Случайная величина ξ с законом распределения (2.6) носит название случайной величины, распределенной по геометрическому закону с параметром р. Для краткости закон распределения обозначают символом G(p).
Пример 5.
Вероятность успешно провести физический
опыт (получить ожидаемый эффект) равна
0.8. Пусть ξ – число «пустых» опытов,
прежде чем экспериментатор получит
ожидаемый эффект. Описать закон
распределения сл. величины
![]() .
.
Решение. ξ – дискретная случайная величина, имеющая геометрическое распределение. Формула (2.6) полностью описывает эту случайную величину при p=0.8, это ее ряд распределения. Изобразим его в виде таблицы:
|
|
0 |
1 |
2 |
3 |
4 |
…. |
|
P |
0.8 |
0.16 |
0.032 |
0.0064 |
0.00128 |
…. |
Замечание.
В литературе по теории вероятностей
случайную величину ξ – номер первого
успеха в серии из n независимых одинаковых
испытаний – также считают распределенной
по геометрическому закону:
![]()
Пусть ξ имеет геометрическое распределение. Тогда
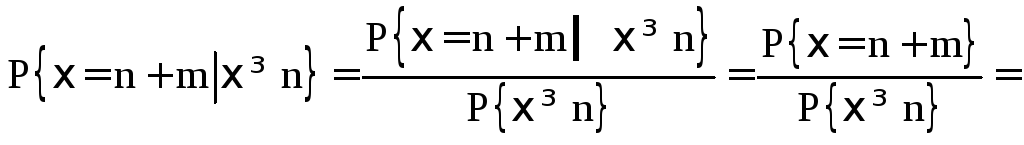
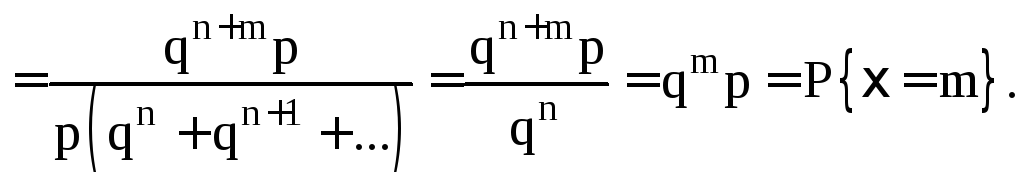
Cвойство сл. величины, выражаемое полученным равенством, называется отсутствием последействия. Его можно интерпретировать следующим образом. Пусть длительность телефонного разговора есть целочисленная величина, и в начале каждой минуты с вероятностью р принимается решение разговор закончить и с вероятностью 1 – р = q принимается решение разговор продолжать. Тогда полученное равенство означает, что условная вероятность того, что разговор будет продолжаться n+m минут, если известно, что он не закончился за n минут, совпадает с вероятностью того, что разговор будет продолжаться m минут. Среди дискретных сл. величин только геометрическое распределение обладает этим свойством.
6. Пуассоновское распределение. В разделе 1.11 мы встречались с формулой Пуассона, ее не надо путать с распределением Пуассона. Случайная величина ξ распределена по закону Пуассона, если она принимает неотрицательные целые значения с вероятностями
![]() (2.7)
(2.7)
где λ > 0 – параметр распределения Пуассона, это среднее значение сл. величины (см. п. 2.5). Обозначается распределение символом Ро(λ).
Равенство![]() выполняется:
выполняется:![]() Это распределение играет важную роль
в теории надежности, теории массового
обслуживания и т.д.
Это распределение играет важную роль
в теории надежности, теории массового
обслуживания и т.д.
Пример
6.
При работе аппарата возникают сбои.
Количество сбоев за сутки – сл. величина
ξ, распределенная по закону Пуассона
или
![]() Среднее число сбоев за сутки равно 1.5.
Определить вероятности событий A = {в
течение суток произошел хотя бы один
сбой},
В = {за двое суток не будет ни
одного сбоя}.
Среднее число сбоев за сутки равно 1.5.
Определить вероятности событий A = {в
течение суток произошел хотя бы один
сбой},
В = {за двое суток не будет ни
одного сбоя}.
Решение. Из
условия задачи и замечания к формуле
(2.7) следует, что λ = 1.5,
![]()
![]()
![]()
7. Гипергеометрическое распределение. С этим распределением мы уже встречались – см. примеры 17, 40 раздела 1.
