2.5. Полнота систем булевых функций

Как уже говорилось выше, система переключательных функций называетсяполной, если всякая переключательная функция является некоторой суперпозицией этих функцийf₁,f₂, ... ,f_n.

Примерами функционально полных систем могут служить следующие системы логических операций:

, ,,,,,,,и др.

Для определения функциональной полноты системы используются так называемые классы Поста.

Классы Поста

1. Класс функций, сохраняющих нуль (P₀). Переключательная функция называетсясохраняющей нуль, еслиf(0,0,...,0)=0.

2. Класс функций, сохраняющих единицу (P₁). Переключательная функция называетсясохраняющей единицу, еслиf(1,1,...,1)=1.

3. Класс самодвойственных функций (S). Функция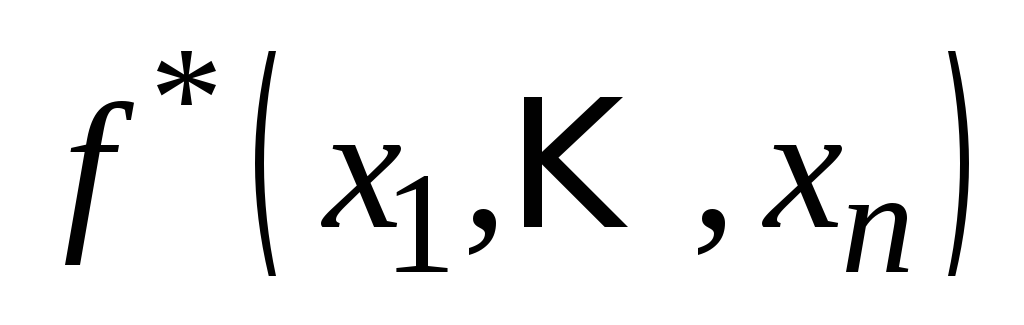называетсядвойственнойк функци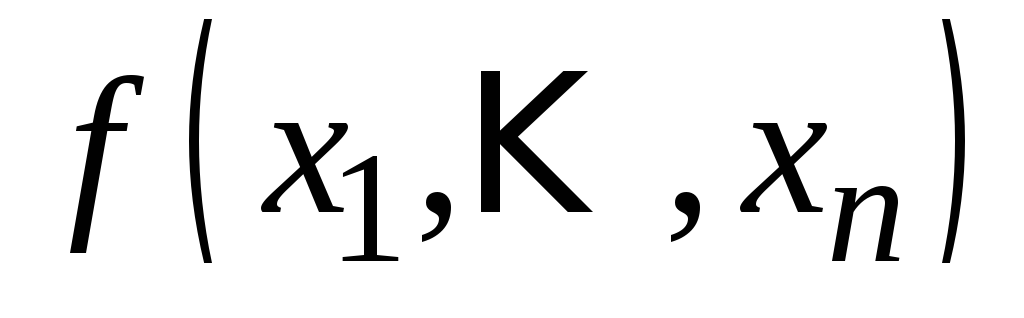и, если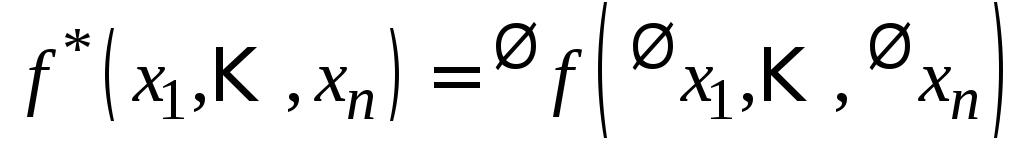. Переключательная функцияназываетсясамодвойственной, если.

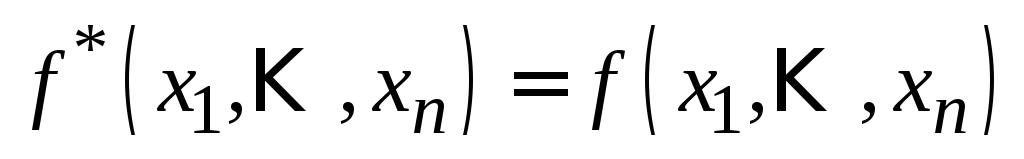4. Класс монотонных функций (M). Переключательная функция называетсямонотонной, еслиf(₁₂ ..._n)f(₁₂..._n) на всех сравнимых наборах, т.е. таких, что (₁₂..._n)(₁₂..._n). Причем (₁₂..._n)(₁₂..._n), если при любомi:_i_i.

5. Класс линейных функций (L). Переключательная функция называетсялинейной, если она представима линейным полиномом Жегалкина.

Теорема 3. Всякая булева функция представимаполиномом Жегалкина, т.е. в виде

f(x₁, x₂,..., x_n)=a₀a₁x₁ a_nx_na_n+1x₁x₂a_2n‑1x₁x_n

a_2nx₂x₃a_kx₁x₂x_n, где a_i{0,1}.

Для доказательства достаточно привести тождества (эквивалентные отношения), позволяющие преобразовать произвольную ДНФ в полином Жегалкина:

1) xy=xyxy,

2)=x1,

3) x=1,

4) x0=x,

5) xx=0,

6) x(yz)=xyxz.

В качестве примера приведем полиномы Жегалкина для конституент 1 функции трёх переменных (см. таблицу 7).

Таблица 7

Полиномы Жегалкина

x y z	Формула конституенты	Полином Жегалкина
0 0 0
0 0 1
0 1 0
0 1 1
1 0 0
1 0 1
1 1 0
1 1 1

Так как конъюнкция конституент разных наборов всегда равна нулю, то справедлива следующая лемма.

Лемма 9. В СДНФ при построении полинома Жегалкина можно все ‘’ заменить на ‘’.

Полином Жегалкина называется линейным, если он не содержит произведения переменных, т.е.a_i=0i>n.

Теорема 4. Если функция принимает значение 1 на нечетном количестве наборов, то она нелинейна.

Доказательство вытекает из таблицы предыдущего примера и леммы 9. Каждая конституента функции «даст» ровно одно слагаемое вида. А сумма по модулю 2 нечетного количества одинаковых слагаемых равна одному слагаемому (так какxx=0), поэтому соответствующий функцииfполином Жегалкина будет содержать конъюнкцию, т.е. будет нелинейным.

Пример 32. Для функцииf(x,y,z,p)=(1000 1101 1111 0100) определить принадлежность классам Поста.

, так как ;

, так как;

, так как;

, так как;

, так как функция имеет нечетное количество единиц.

Лемма 10. Каждый класс Поста замкнут относительно операций подстановки и суперпозиции, т. е. с помощью этих операций можно получить только функции того же класса Поста.

Теорема Поста (сильная).Система переключательных функций тогда и только тогда является функционально полной, когда для каждого классаP₀,P₁,S,M,Lв ней найдется функция, не принадлежащая этому классу.

Теорема Поста (слабая).Система переключательных функций, содержащаяconst0 иconst1, является функционально полной тогда и только тогда, когда она содержит хотя бы одну нелинейную и хотя бы одну немонотонную функцию.

Система функций Fназываетсянезависимой, если никакая функцияfFне представима суперпозициями функций изF\{f}. Независимая система функций называетсябазисом классаK, если всякая функция изKесть суперпозиция функций изF, или, другими словами, система переключательных функций называетсябазисом, если она функционально полная, а удаление любой функции из этой системы делает ее неполной.

Теорема 5. Каждый базис функционально полной системы содержит не более 4 булевых функций.

Для доказательства рассмотрим четыре случая:

1. Система не содержит функций const0 и const1. Но по сильной теореме Поста в ней должна быть функцияf, не сохраняющая 0. Так как это не может бытьconst1, то эта функция является также немонотонной. Поэтому, чтобы получить базис, достаточно кроме функцииfвключить в базис системы одну несамодвойственную, одну нелинейную и одну не сохраняющую 1 функции. А, следовательно, базис функционально полной системы будет содержать не более 4 функций.

2, 3. Система содержит одну из функций const0 илиconst1. Достаточно отметить, что обе функцииconst0 иconst 1 являютсянесамодвойственными. Далее доказательство аналогично случаю 1.

4. Система содержит обе функции const0 и const1. Доказательством в этом случае служит слабая теорема Поста.

Пример 33. Выписать все базисы, содержащие функции из совокупности, если принадлежность классам Поста для этих функций указана в таблице (« + »означает, что функция принадлежит соответствующему классу, а ­ « – » – не принадлежит):

	P0	P1	S	M	L
	+	–	–	–	–
	–	+	–	–	–
	+	–	–	+	+
	+	+	–	+	–
	–	+	–	–	+
	+	–	–	–	+

Базисы:

, ,

, ,

,.