5)Геометрическая интерпретация основной задачи оптимального управления

Основным задачам оптимального управления при закрепленных концах можно дать следующую эквивалентную геометрическую формулировку.

Пусть при t = t0 задано начальное состояние x0 = x(t0) , а при t = t1 – конечное состояние x1 = x(t1) , где t0, t1, x0, x1 – фиксированные значения. Тогда в функционале J[u] (4) слагаемое Φ(t0, t1, x0, x1) является известным числом Φ0 . Введем новую переменную x0, закон изменения которой имеет вид

с начальным условием

Присоединим эту переменную к системе (1). Тогда при t = t0 система находится в точке (x0(t0), x1(t0), ..., xn(t0))T , а при t = t1 – в точке (x0 (t1), x1(t1), ..., xn (t1))T , где

Таким образом, если в (n + 1)-мерном пространстве точек (x0,x) провести через точку (0, x1) прямую П параллельно оси x0 0, то решение системы (1), (10) проходит при t = t1 через точку на прямой П с координатой x0(t1) = J . Теперь основная задача оптимального программного управления формулируется геометрически как на рис. 6.

Рис. 6. Геометрическая формулировка основной задачи

оптимального управления:

1 – оптимальная траектория; 1' – изменение критерия качества J вдоль

оптимальной траектории; 2, 3 – неоптимальные траектории, проходящие через точки (x0, t0), (x1, t1); 2', 3' – изменение критерия качества J

вдоль неоптимальных траекторий

В (n + 1)-мерном фазовом пространстве (x0, x1, ..., xn)T даны:

1) при t = t0 точка (Φ0, x0) ;

2) прямая П, параллельная оси 0x0 и проходящая через точку (0, x1) .

Среди всех допустимых программных управлений u = u(t), обладающих тем свойством, что соответствующее решение xxtt0 (( ,)()) системы (1), (10) с начальным условием (Φ0, x1(t0), ..., xn(t0))T пересекает при t =t1 прямую П, найти такое, для которого точка пересечения с прямой П имеет наименьшую (наибольшую) координату x0(t1) = J .

6) Эквивалентные преобразования озу и условия существования решения

Вместо функционалов J_i (1) введем безразмерные по формулам:

(3)

Величина характеризует относительное удалениеJ_i от границы А_i, а - от границыa_i. Сумма иравняется единице т. е.:

(4)

Из выражения (3) следует, что если

, (5)

то (6)

Используя (4) и (5) получим, что если

, (7)

то (8)

и выполняются неравенства (5).

Аналогично из (8) следуют неравенства (5) и (7). Таким образом, неравенства (5), (7), (8) эквивалентны. Равенство (4) можно записать в виде:

(9)

Это равенство определяет расположение функционалов на числовой оси, а именно: при одинаковом управлении функционалы расположены на числовой оси симметрично относительно точки 0.5, см.

Если, например, при каком-либо управлении окажется, что =3, то должно быть=-2, или если=0,7, то=0,3.

Отсюда видно, что в каждой паре функционалов при одинаковом управлении всегда один больше другого, кроме единственного случая, когда ==0,5. Ясно, что в этом случае фазовая траектория проходит как раз через середину между верхним и нижним ограничением.

В дальнейшем вместо (5) будем пользоваться неравенствами (8). Но предварительно введем обозначения:

Тогда неравенства (8) запишутся в виде:

(10)

Суть этих преобразований в том, что двухсторонние неравенства (5) заменены односторонними, функционалы безразмерными и предел изменения одинаков и равен единице.

Основная задача управления запишется теперь в виде:

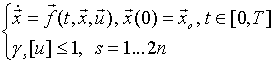(11)

Решение этой задачи, если оно существует, обычно не единственное. Задача может и не иметь решения. При этом ограничения, наложенные на ипротиворечивы.