5. Нестационарные процессы теплопроводности

Выше были рассмотрены условия распространения теплоты при стационарном режиме, когда температурное поле во времени не менялось, оставаясь постоянным. Если же температурное поле меняется во времени, т.е. является функцией времени, то протекающие в таких условиях тепловые процессы, называются нестационарными.

Скорость теплового процесса при нестационарном режиме определяется значением коэффициентом температуропроводности , который здесь имеет такое же важное значение, как и коэффициент теплопроводности при стационарном режиме.

Решить задачу нестационарной теплопроводности – это, значит, найти зависимости изменения температуры и количества переданной теплоты во времени для любой точки тела. Такие зависимости могут быть получены путем решения дифференциального уравнения теплопроводности. Аналитическая теория ставит себе целью получение общего решения задачи. Такие решения получаются достаточно сложными даже для тел простой формы: пластины, цилиндра и шара.

1.5.1. Аналитическое описание процесса

Аналитическое описание процесса теплопроводности включает в себя дифференциальное уравнение и условие однозначности.

Дифференциальное уравнение теплопроводности в декартовой системе координат при отсутствии внутренних источников теплоты имеет вид:

. (1.122)

Условия однозначности задаются в виде:

• теплофизических параметров: ,, и;

• формы и геометрических размеров объекта: ,,…,;

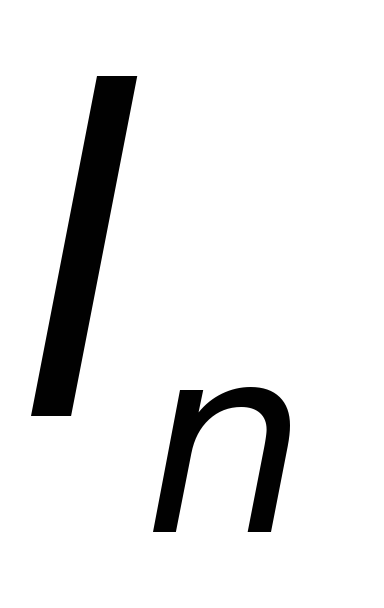• температура тела в начальный момент времени ;

• граничные условия.

Граничные условия могут быть заданы в виде граничных условий третьего рода:

.

Дифференциальное уравнение теплопроводности с условиями однозначности даст законченную математическую формулировку рассматриваемой задачи. Решение ее заключается в отыскании функции:

. (1.123)

Охлаждение (нагревание) неограниченной пластины

Рассмотрим плоскую пластину толщиной (см. рис. 1.16). Заданы теплофизические параметры пластины:,, и. Если толщина пластины мала по сравнению с длиной и шириной, то такую пластину обычно считают неограниченной. При заданных граничных условиях коэффициент теплоотдачиодинаков для всех точек поверхности пластины. Изменение температуры происходит только в одном направлении, в двух других направлениях температура не изменяется, следовательно, в пространстве задача является одномерной. В начальный момент времени пластина имеет по всему сечению одинаковую температуру. Охлаждение происходит в среде с постоянной температурой. На обеих поверхностях отвод тепла осуществляется при постоянном во времени коэффициенте теплоотдачи. Отсчет температуры пластины для любого момента времени будем вести от температуры окружающей среды, т.е.. Так как задача в пространстве одномерная, то дифференциальное уравнение примет вид:

. (1.124)

Рис. 1.16. Охлаждение неограниченной пластины

Для переменной начальные условия примут вид:

. (1.125)

При заданных условиях охлаждения задача становится симметричной и начало координат удобно поместить на оси пластины, как показано на рис 1.16.

При этом

при. (1.126)

Из симметрии температуры следует, что

при. (1.127)

Таким образом, достаточно определить температуру для одной половины, например для правой, а в левой половине воспользоваться условием (1.126) в тот же момент времени.

Граничное условие на поверхности пластины при запишется

при. (1.128)

Решением дифференциального уравнения (1.124) с учетом начальных и граничных условий будет

здесь:

. (1.143)

Характеристическое уравнение (1.143) имеет бесконечное множество решений ,, … ,, … (см рис. 1.17).

Рис. 1.17. К решению уравнения (1.143)

. (1.150)

Иногда бывает удобно уравнение (1.150) записать в безразмерном виде:

, (1.151)

где ;;– число Фурье, представляющее собой безразмерное время.

Анализ полученного решения

Так как ,,, …,, представляют собой ряд возрастающих чисел, то чем больше, тем меньше роль последующего члена ряда по сравнению с предыдущим. Кроме того, чем больше число, тем члены ряда будут убывать быстрее с увеличением номера.

Численные расчеты показали, что уже при ряд становится настолько быстро сходящим, что распределение температуры достаточно точно описывается первым членом ряда:

 . (1.152)

В условиях охлаждения пластины (при ) для любого момента времени при заданных граничных условиях поле температуры имеет вид симметричной кривой с максимумом на оси пластины (). Для каждого последующего момента времени будет своя кривая, монотонно убывающая к поверхности пластины. При этом для любого момента времени касательные к кривым в точкахпроходит через две направляющие точкии, расположенных на расстоянииот поверхности пластины,(см. рис. 1.18).

Для доказательства этого важного свойства рассмотрим температурное поле для произвольного момента времени .

Умножив граничные условие на, получим

. (1.153)

В безразмерном выражение (1.153) запишется

. (1.154)

Из рис. 1.18 следует, что

. (1.155)

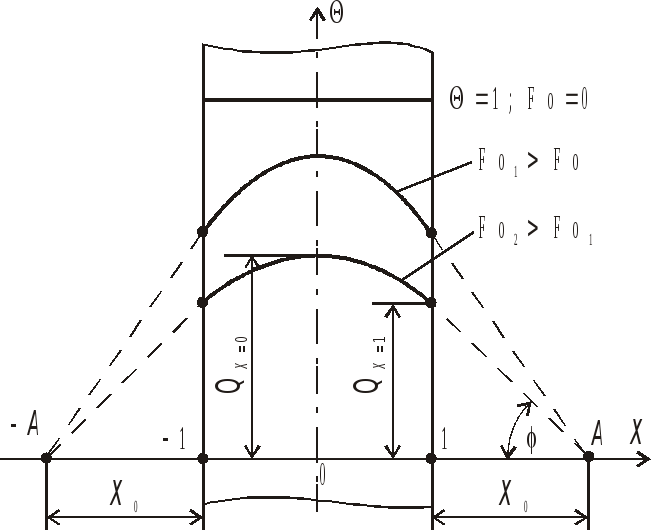
Рис.1.18. Изменение температурного поля в плоской неограниченной стенке при ее охлаждении

Сравнивая выражения (1.154) и (1.155), получаем:

. (1.156)

Из уравнения (1.156) следует, что расстояние от точки до поверхности пластины определяется заданными условиями однозначности, которые справедливы для любого момента времени. Следовательно, касательные ко всем температурным кривым в точке пересечения с поверхностью пластины и неизменных граничных условиях всегда будут проходить через т. . Этот вывод справедлив и для тел других геометрических форм.

При (практически при). Данный режим охлаждения реализуется при. Граничное условие третьего рода вырождается в граничное условие первого рода. Тогда распределение температур будет таким, как это показано на рис.1.19.

Рис. 1.19. Распределение температуры в плоской стенке при ее охлаждении в условиях

При (практически при). Малые значения числамогут иметь место при малых размерах толщины пластины при большихи малых. При малыхтемпература на поверхности пластины незначительно отличается от температуры на оси. Это указывает на то, что температура по толщине распределяется равномерно и кривая температур остается практически параллельной осидля любого момента времени (см. рис. 1.20). На рисунках 1.19 и 1.20.

Когда число находится в пределах,есть некоторая конечная величина (см. рис. 1.18).

Рис.1.20. Распределение температуры в плоской стенке при ее охлаждении в условиях

Регулярный режим охлаждения или нагревания тел

Если безразмерное время (число Фурье ) больше 0,3, то процесс охлаждения из неупорядоченной стадии переходит в стадию регулярного режима.

При регулярном режиме охлаждения изменение температурного поля рассматриваемого тела во времени принимает простой и универсальный вид

, (1.11)

Тогда

. (1.12)

Из уравнения (1.12) следует, что натуральный логарифм избыточной температуры для всех точек тела изменяется во времени по линейному закону.

Величина m, 1/с, есть положительное число, не зависящее от координат и времени. Эта величина характеризует интенсивность охлаждения (нагревания) тела и называется темпом охлаждения (нагревания).

Темп охлаждения однородного тела при конечном значении коэффициента теплоотдачи пропорционален коэффициенту теплоотдачии внешней поверхности телаи обратно пропорционален полной теплоемкости тела:

, (1.13)

здесь – коэффициент неравномерности распределения температуры в теле и зависит от условий охлаждения на поверхности тела,.

Величина определяется по формуле

, (1.14)

где – модифицированное число Био.

, (1.15)

где – коэффициент формы.

Для тел простой формы величина определяются по аналитическим формулам

для шара

;

для цилиндра длиной

;

для параллелепипеда со сторонами ,,

.

Темп охлаждения можно определить: из аналитического решения; графически; по формуле (1.13).

Рис. 1.22. Зависимость от времени при охлаждении (нагревании) тел