17. Обходы графов, эйлеровы и гамильтоновы графы, алгоритм Флери. Укладки графов, изоморфизм, гомеоморфизм, планарность, критерий планарности, формула Эйлера.

Граф – совокупность непустого множества вершин и множества ребер (дуг), объединяющих две вершины.

Виды:

• Двудольный граф – граф, в котором вершины можно разбить на два непересекающихся подмножества V₁ и V₂ так, что всякое ребро соединяет вершину из V₁ с вершиной из V₂.

• Полный граф – граф, в котором любые две (различные, если не допускаются петли) вершины соединены ребром.

• Планарный граф – граф, который можно изобразить на плоскости без пересечений рёбер.

• Связный граф — граф, содержащий ровно одну компоненту связности. Это означает, что между любой парой вершин этого графа существует как минимум один путь.

• Мультиграф – граф, в котором допускаются и кратные ребра, и петли.

Эйлеровым циклом в графе называется цикл, проходящий через все ребра графа ровно по одному разу.

Первая теорема Эйлера. Граф содержит эйлеров цикл тогда и только тогда, когда в нем все вершины имеют четную степень.

Эйлерова цепь – цепь, сединяющая 2 различные вершины, проходящая через все ребра графа ровно по одному разу.

Теорема 2. В графе существует эйлерова цепь тогда и только тогда, когда 2 вершины имеют нечетную степень.

Алгоритм Флери (нахождение эейлрова цикла):

1. Найти вершину нечетной степени и считать ее начальной вершиной обхода/цепи

2. Из начальной вершины выходим по любому ребру, не являющемуся мостом. Удаляем это ребро

3. Из текущей вершины выходим по любому ребру, не являющемуся мостом, удаляем это ребро. Если такого ребра нет, идем по мосту

4. Повторяем в цикле п.3, пока не удалим все ребра

Мост в графе – ребро, после удаления которого увеличивается количество компонент связности графа.

Компонента связности - некоторое множество вершин графа такое, что для любых двух вершин из этого множества существует путь из одной в другую, и не существует пути из вершины этого множества в вершину не из этого множества.

Гамильтонов цикл – цикл, проходящий через все вершины ровно один раз.

Гамиьтонова цепь – аналогично.

Утверждение. Достаточное условие существования гамильтонова цикла: если в связном n-вершинном графе, где n>=3, выполняется неравенство: степень вершины >= n/2, то в графе существует гамильтонов цикл.

Изоморфизм и гомеоморфизм

Графы называются изоморфными, если между множествами их вершин можно установить взаимооднозначное соответствие, сохраняющее смежность вершин.

Двум смежным вершинам 1 графа соответствуют всегда смежные вершины 2 графа, а двум несмежным вершинам 1 графа всегда соответствуют несмежные вершины 2 графа.

Доказательство изоморфности графов: достаточно предъявить хотя бы одно взаимооднозначное соответствие, сохраняющее смежность.

Доказательство неизоморфности графов: достаточно найти существенное отличие между графами (разное число вершин, ребер, разный набор степеней вершин, радиус, диаметр, количество циклов определенной длины).

Два графа гомеоморфны, если в результате их стягивания получаются изоморфные графы.

При стягивании графа исчезают все вершины степени 2.

Если графы гомеоморфны, то либо оба эти графа планарны, либо оба непланарны.

Планарные графы

Граф называется планарным, если его можно нарисовать на плоскости без пересечения ребер.

К₄ – планарный граф

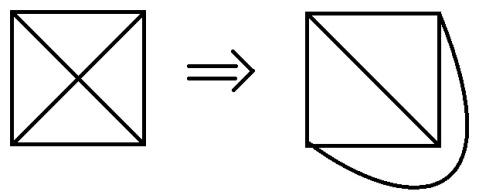
Теорема (критерий планарности):

Граф планарен тогда и только тогда, когда в нем нет подграфов гомеоморфных графу К₅ или К₃₃.

Графы К₅ и К₃₃

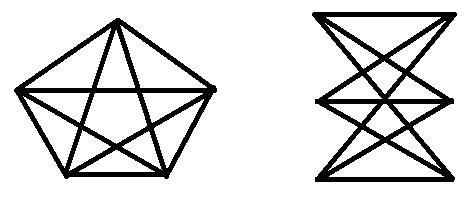
Чтобы доказать, что граф непланарен, нужно найти в нем подграф, гомеоморфный графу К₃₃ или К₅.

Признаки планарности:

• Если граф планарен, в нем обязательно найдется вершина степени не выше 5

• В любом связном планарном графе, содержащем не менее 3 вершин, выполняется неравенство n<=3m-6, где n – число вершин, m – число ребер.

• Формула Эйлера:

n+g=m+k+1, где n – количество вершин

g – количество граней

m – количество ребер

k – количество компонент связности

• Формула для связного графа: n+g=m+2