20. Раскраски графов, «жадный» алгоритм. Хроматическое число, хроматический многочлен, его нахождение и свойства.

Правильная раскраска графа – такое соответствие между множеством вершин и множеством красок, при котором любым 2м смежным вершинам соответствуют разные цвета.

Минимальное количество цветов, достаточное для правильной раскраски графа, называется хроматическим числом графа.

«жадный» алгоритм для вычисления хроматического числа (может дать неправильный ответ).

1. Пронумеруем вершины: берем первый цвет и красим вершину в этот цвет

2. Идем по всем остальным вершинным в порядке их номеров и красим их в 1й цвет

3. К 1й краске больше не возвращаемся

4. Красив в цвет 2 все непокрашенные вершины правильным образом в порядке возрастания номеров

5. дальше берем следующий цвет и повторяем п.4

Хроматический многочлен графа G – это многочлен P(G,x), который при каждом N “x”равен количеству различных правильных раскрасок графа с использованием не более, чем x цветов.

Для n-вершинного дерева:

P(G,x)=x(x-1)^n-1

Например: К₃P(K₃,x)=x(x-1)(x-2)

K₄P(K₄,x)=x(x-1)(x-2)(x-3)

Граф G⁺ получается из графа G добавлением ребра, соединяющего две несмежные вершины.

Граф G^- получается из графа G отождествлением тех же двух вершин.

Для любого графа G его хроматический многочлен удовлетворяет равенству:

P(G,x)=P(G⁺,x)+P(G^-,x)

Свойства:

• Степень многочлена всегда равна количеству вершин

• В n-вершинном графе коэффициент при x^n-1 всегда отрицательный и по модулю равен количеству ребер в графе

• Знаки коэффициентов чередуются

• Хроматическое число графа на 1 больше, чем максимальный корень хроматического многочлена

Теорема о пяти красках. Любой планарный граф можно покрасить правильным образом, используя 5 цветов.

21. Элементарные булевы функции и способы их задания, существенные и фиктивные переменные. Разложение булевых функций по переменным, сднф, скнф, полиномы Жегалкина.

Функция f(x₁, x₂, …, x_n) называется булевой функцией, если каждому набору x₁, x₂, …, x_n, состоящему из 0 и 1, она ставит в соответствие число f(x₁, x₂, …, x_n), равное 0 или 1.

Элементарные функции (самим написать таблицы истинности)

Логическое отрицание (функция НЕ). 

Обозначения: ¬x. Запись ¬x читается «не икс» или «отрицание икс».

Логическое умножение (конъюнкция). Функция минимума

Обозначения: x&y, x⋅y, min(x,y). Запись x&y может читаться так: «икс и игрек» или «икс умножить на игрек».

Логическое сложение (дизъюнкция). Функция максимума.

Обозначения: x∨y, max(x,y). Запись x∨y может читаться так: «икс или игрек» или «сумма икс и игрек».

Эквивалентность

Обозначения: x∼y, x↔y. Запись x∼y может читаться так: «икс эквивалентно игрек» или «икс равносильно игрек».

ИСКЛЮЧАЮЩЕЕ ИЛИ (операция антиэквивалентность или СЛОЖЕНИЕ ПО МОДУЛЮ ДВА). 

Обозначения: x⊕y, x+y. Запись x⊕y может читаться так: «икс плюс игрек».

x	0	0	1	1
y	0	1	0	1
f(x, y)	0	1	1	0

Импликация (логическое следование).

Обозначения: x→y, x⇒y, x⊃y. Запись x→y может читаться так: «из икс следует игрек».

x	0	0	1	1
y	0	1	0	1
f(x, y)	1	1	0	1

Штрих Шеффера (отрицание конъюнкции, логическое «не-и»)

Обозначение: x|y. Запись x|y может читаться так: «не икс или не игрек», «икс и игрек несовместны», «икс штрих Шеффера игрек».

x	0	0	1	1
y	0	1	0	1
f(x, y)	1	1	1	0

Стрелка Пирса (отрицание дизъюнкции, логическое «не-или», функция Вебба)

 Обозначение: x↓y; для функции Вебба - x°y. Запись x↓y может читаться так: «ни икс и ни игрек», «икс стрелка Пирса игрек».

x	0	0	1	1
y	0	1	0	1
f(x, y)	1	0	0	0

Способы задания функции

1. Табличный

2. С помощью формулы

3. Векторный

4. Графический

5. С помощью карты Карно

6. С помощью схем из функциональных элементов

Опр. Переменная x_i называется существенной переменной для булевой функции f(x₁, x₂, …, x_n), если существует набор (a, a₁, …, a_i-1, 0, a_i+1, …, a_n), такой что f(a, a₁, …, a_i-1, 0, a_i+1, …, a_n) не равна f(a, a₁, …, a_i-1, 1, a_i+1, …, a_n).

Опр. Переменная x_i называется фиктивной (несущественной) переменной для булевой функции f(x₁, x₂, …, x_n), если для любого набора (b, b₁, …, b_i-1, b_i+1, …, b_n) верно f(b, b₁, …, b_i-1, 0, b_i+1, …, b_n)=f(b, b₁, …, b_i-1, 1, b_i+1, …, b_n).

Если переменная не существенна, то можно подобрать такую формулу для это функции, в которую не входит эта переменная.

Разложение булевых функций в формулы специального вида.

1. СДНФ (совершенная дизъюнктивная нормальная формула)

СДНФ для булевой функции f(x₁, x₂, …, x_n) – это дизъюнкция, в которой каждое слагаемое имеет вид .

Форма называется совершенной, т.к. все x содержатся в каждом множителе.

Утв. Любую булеву функцию, не равную тождественно нулю, можно представить в виду СДНФ.

2. СКНФ (совершенная конъюнктивная нормальная формула)

СКНФ для булевой функции – это конъюнкция, в которой каждый множитель имеет вид

.

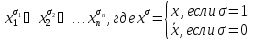Утв. Любую булеву функцию, не равную тождественно 1, можно представить в виду СКНФ.

3. Полином Жегалкина

Сумма по модулю 2, в которой каждое слагаемое является

а) const 1

b) произведением некоторых переменных (отрицание переменных запрещается)

Утв. Любую булеву функцию можно представить в виде полинома Жегалкина (при этом фиктивные переменные в полином Жегалкина не входят).

Полином Жегалкина можно получить помощью эквивалентных преобразований ДНФ

По сравнению с ДНФ в полиноме Жегалкина отсутствуют операции ИЛИ и НЕ. Таким образом, полином Жегалкина можно получить из ДНФ, выразив операции ИЛИ и НЕ через операции сложение по модулю два, и константу 1. Для этого применяются следующие соотношения:

Ниже приведён пример преобразования ДНФ в полином Жегалкина:

При преобразованиях использованы соотношения: