Контрольная работа №1 (30 вариантов)

1. Решить систему уравнений по формулам Крамера, методом обратной матрицы и методом Гаусса. Выполнить проверку для одного из методов решения.

2. Найти пределы функций.

3. Даны координаты вершин пирамиды А_1, А_2, А_3, А₄. Средствами векторной алгебры найти:

1. Объем пирамиды А₁ А₂ А₃ А₄;

2. Длину ребра А₂ А₃;

3. Площадь грани А₁ А₂ А_3;

4. Угол между ребрами А₁ А₂ и А₁ А₄.

4. Даны две системы векторов Определить, какая из этих систем образует базис; разложить вектор по этому базису.

5. Вычислить приближенно с помощью дифференциала.

6. Найти пределы, пользуясь правилом Лопиталя.

7. Исследовать функцию и построить ее график.

Общая схема исследования функции

1. Найти область определения функции (ООФ).

2. Исследовать функцию на четность, нечетность.

3. Исследовать поведение функции на границах ООФ (точки разрыва, характер разрывов, вертикальные асимптоты, пределы функции в граничных точках ООФ или при x → +∞, x → ∞).

4. Найти наклонные и горизонтальные асимптоты.

5. Установить точки пересечения графика функции с осями координат (если возможно), интервалы знакопостоянства функции.

6. Установить интервалы монотонности и экстремумы функции.

7. Найти интервалы выпуклости и вогнутости, точки перегиба.

8. По результатам исследования построить график.

Вариант №1

Вариант №2

Вариант №3

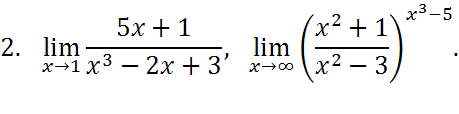
Вариант №4

Вариант №5

Вариант №6

Вариант №7

Вариант №8

Вариант №9

Вариант №10

Вариант №11

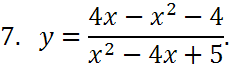
Вариант №12

Вариант №13

Вариант №14

Вариант №15

.

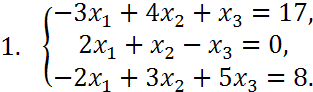
Вариант №16

Вариант №17

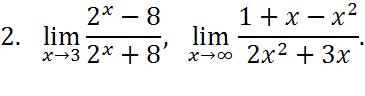
Вариант №18

7.

Вариант №19

Вариант №20

5. 

7. 

Вариант №21

Вариант №22

Вариант №23

Вариант №24

1. 

Вариант №25

Вариант №26

Вариант №27

7.

Вариант №28

Вариант №29

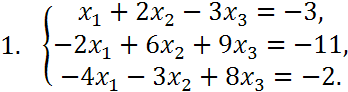
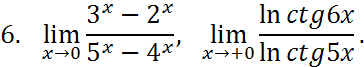
Вариант №30

Методические указания к выполнению контрольной работы №1

Задача 1.

а) Решить систему линейных уравнений по формулам Крамера, выполнить проверку.

Решение. Составим из коэффициентов при неизвестных главный определитель системы:

Вычислим его одним из способов (метод треугольников или метод дополнений):

Главный определитель системы отличен от нуля, значит, система совместна.

Вычислим вспомогательные определители, которые получаются из главного, заменой соответствующих столбцов на столбец свободных членов:

;

;

.

Решение системы находится по формулам Крамера:

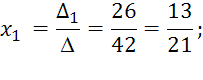
Проверка. Подставим найденное решение в систему уравнений:

Ответ: .

б) Решить систему линейных уравнений с помощью обратной матрицы.

Решение. В матричной форме систему линейных уравнений можно записать так: AX = B, где A – матрица коэффициентов системы; X – матрица-столбец неизвестных; B – матрица-столбец свободных членов. Умножив слева обе части равенства AX = B на A^-1(A^-1существует, если ), получим

A^-1AX=A^-1B; EX=A^-1B; X=A^-1B,

здесь E – единичная матрица.

Следовательно, чтобы найти решение системы n линейных уравнений с n неизвестными при помощи обратной матрицы, нужно матрицу, обратную матрице из коэффициентов системы, умножить на матрицу-столбец свободных членов. В результате получаем матрицу-столбец, которая и будет решением данной системы.

Найдём определитель матрицы A:

, следовательно, матрица A обратима.

,

где A_ij - алгебраические дополнения элементов a_ij данной матрицы.

Найдём алгебраические дополнения для элементов данной матрицы:

;

;

;

;

.

Обратная матрица имеет вид:

.

Необходимо сделать сверку: AA^-1 = E.

.

Найдём решение системы X=A^-1B:

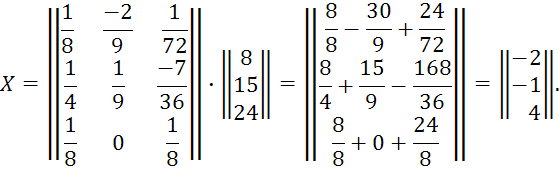
x₁ = 2; x₂ = 1; x₃ = 4.

Ответ:

в) Решить методом Гаусса систему уравнений:

Решение:

1-й шаг – формирование первого столбца.

Первую строку расширенной матрицы умножим на 2 и прибавим ко второй строке, также первую строку умножим на (3) и прибавим к третьей строке рас­ширенной матрицы. После этого все элементы первого столбца матрицы, кроме первого, окажутся равными нулю:

x1	x2	x3		(2)(-3)	x1	x2	x3
1	1	1	6		1	1	1	6
2	1	4	8	~	0	1	6	20
3	2	1	4		0	1	4	14

2-й шаг – формирование второго столбца.

Вторую строку, умноженную на (1), прибавим к первой строке, вторую строку прибавим к третьей строке расширенной матрицы. После этого все элементы второго столбца матрицы, кроме диагонального, окажутся равными нулю:

x1	x2	x3			x1	x2	x3
1	1	1	6		1	1	5	14
0	1	6	20	(1)(1)	0	1	6	20
0	1	2	6	~	0	0	2	6

3-й шаг – формирование третьего столбца.

Третью строку разделим на 2, чтобы ее диагональный элемент равнялся единице. После этого третью строку, умноженную на (6), прибавим ко второй, и третью строку, умноженную на 5, прибавим к первой строке:

x1	x2	x3			x1	x2	x3			x1	x2	x3
1	0	5	14		1	0	5	14		1	0	0	1
0	1	6	20	~	0	1	6	20		0	1	0	2
0	0	2	6	:(2)	0	0	1	3	(6)(5) ~	0	0	1	3

Система, которая соответствует полученной расширенной матрице, имеет вид:

и решение ее очевидно:

Ответ:

Задача 2.

Найти пределы функций:

Решение:

1) вначале убеждаемся, что предел функции нельзя найти непосредственной подстановкой, что при указанном изменении аргумента она представляет отношение двух бесконечно малых величин (неопределенность вида ). Затем делаем преобразования, чтобы сократить дробь на множитель, стремящийся к нулю.

Разлагаем числитель и знаменатель на множители. Затем сокращаем дробь на (x  5). Аргумент x стремится к своему предельному значению, но не совпадает с ним, поэтому множитель (x  5) отличен от нуля при x → 5

2) при основание стремится к 1, а показатель степени (4x + 1) стремится к бесконечности. Следовательно, имеем неопределённость вида Представим основание в виде суммы 1 и некоторой бесконечно малой величины:

Положим 2x + 3 =  4y при x → + ∞ переменная y →  ∞. Выразим показатель степени через новую переменную y.Так как 2x =  4y  3, то 4x + 1 =  8y 5. Таким образом,

3) при x → 2 основание стремится к единице, а показатель степени стремится к бесконечности.

Положим , где Тогда

Задача 3.

Средствами векторной алгебры найти:

1. объём пирамиды с вершинами A₁ A₂ A₃ A _4;

2. длину ребра A₂ A_3;

3. площадь грани A₁ A₂ A_3;

4. угол между рёбрами A₁ A₂ и A₁A _4.

Даны координаты вершины пирамиды:

A₁ (5,1,4); A₂ (1,2,1); A₃ (3,3,4); A ₄(2, 2, 2).

Решение. Построим схематически данную пирамиду (рис.1).

1. Рассмотрим векторы , и . Зная координаты точек, вычислим координаты этих векторов:

;

;

.

Объём пирамиды равен модулю одной шестой доли смешанного произведения векторов , и .

=

2. Найдём длину ребра

3. Вычислим площадь грани A₁ A₂ A_3.

Площадь A₁ A₂ A₃ равна половине площади параллелограмма, построенного на векторах и . Площадь параллелограмма, построенного на векторах и совпадает с модулем векторного произведения а поэтому площадь ∆A₁ A₂ A₃:

4. Найдём угол между рёбрами A₁ A₂ и A₁A _4. Угол φ между векторами и вычислим по формуле:

По таблицам

Ответ: Vпир. = 4 куб. ед.; ;

Задача 4.

Даны две системы векторов:

Определить, какая из этих систем образует базис; разложить вектор по этому базису.

Решение. Используем признак линейной независимости для векторов с числовыми координатами. Найдём определитель:

следовательно, система векторов линейно независима и образует базис.

Вычислим определитель для второй системы:

Система линейно независима.

Проведём разложение вектора .

Запишем разложение вектора в координатной форме:

Получаем систему линейных уравнений:

Систему можно решать любым методом. Решим методом последовательного исключения неизвестных:

Итак, координаты вектора в новом базисе будут а разложение вектора по базису имеет вид .

Ответ: .

Задача 5.

Вычислите приближенно с двумя десятичными знаками .

Решение. Введем функцию f(x) = и в качестве х возьмем число, наибо­лее близкое к 7,28, но такое, чтобы легко вычислялся, и х было бы достаточно малым.

В нашем случае удобно взять х = 8, тогда х = 7,28  8 =  0,72.

Найдем

Вычислим

Тогда по формуле

Ответ:

Задача 6.

Решение.

Имеем неопределенность вида, так как под знаком предела стоит отношение двух бесконечно малых функций. Применяем пра­вило Лопиталя.

Ответ: .

Решение.

Под знаком предела стоит отношение двух бесконечно малых, то есть имеет место неопределенность вида . Применяем правило Лопиталя.

Неопределенность вида сохранилась. Применяем правило Лопиталя еще раз:

Ответ:.

Решение.

Под знаком предела стоит разность двух бесконечно больших од­ного знака, то есть имеет место неопределенность вида . Преобразуем ее к виду и применим правило Лопиталя.

Ответ: 0.

Задача 7.

Исследуйте функцию и постройте ее график.

Решение.

1. Область определения функции D(y) = ( ∞,0) U (0,+ ∞).

2.

Следовательно, данная функция ни четная, ни нечетная.

3. Функция непрерывна в области определения, как частное двух непрерывных функций. Исследуем точку х = 0:

Поэтому х = 0 – точка разрыва функции с бесконечным скачком, а прямая х = 0 – вертикальная асимптота графика функции.

4. Вычислим пределы у (х) при .

Следовательно, прямая у = 0 – левосторонняя горизонтальная асимптота гра­фика.

Правосторонней горизонтальной асимптоты не существует. Будем искать правостороннюю наклонную асимптоту.

При x→∞ нет асимптоты ни горизонтальной, ни наклонной.

5. Находим

Производная равна нулю в точке х = 1.

Составляем таблицу.

x	(∞,0)	(0,1)	1	(1,+∞)
y'			0	+
y			e
			min

6. Найдем вторую производную.

у" не обращается в нуль ни в одной точке, так как е^х > 0, при всех х. Но у" не существует в точке х = 0.

Составляем таблицу.

x	( ∞,0)	(0,+ ∞)
y'’		+
график

7. Точка х = 0 не входит в область определения. Поэтому график не пересекает ось OY.

Уравнение у = 0 не имеет решений, так как е^х > 0 при всех х. Следовательно, ось ОХ график тоже не пересекает. Функция отрица­тельна при х < 0 и положительна при х > 0. Найдем несколько до­полнительных точек для построения графика.

x	3	 2	 1	2	3	0,5	 0,5
y	 0,02	 0,07	 0,37	3,69	6,66	 1,21	3,30