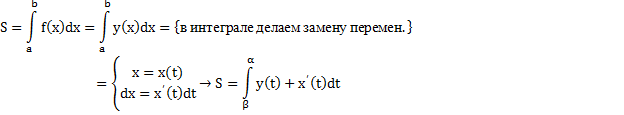6. Определенный интегрл,приложение. Несобственный интеграл.
6.1 Интегральная сумма. Определенный интеграл.
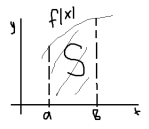
Рисс.1) На отрез [а,в]задана неприр. ф-я Разобьем отрез. [а,в]произвольным образом на n частей:
а=хо; х1,х2,…….хn-1,хn, при этом хo<х1<х2<…<хn
Обозначим ∆х1=х1-х0; ∆х2=х2-х1

,….., ∆xn=xn-xn-1 –длины типичных отрезков
На каждом из частичн. отр. [xi-1;xi], где i=1,2,….,n
Произвольным образом выбираем точку Сi
В каждой из этих точек вычислим значение ф-ии f(c1),f(c2)….,f(cn) и составим сумму :
??n=f(c1)*
∆x1+f(c2)*
∆x0+…..+f(cn)*
∆xn![]() (6.1.1)
(6.1.1)
Опред.: эта сумма назыв. Интегральной суммой для ф-ии f(x) yf jnh [a;b]
Гео метрический смысл интегральной суммы
Интегр.сумма зависит от способа разбиения отр. [a;b] на частичные отрезки [xi-1;xi] и выбора опорных точек Сi внутри частичных отрезков.
Обозначим ![]() наибольшую из длин отрезков при данном
разбиение.
наибольшую из длин отрезков при данном
разбиение.
Рассмотрим некоторые
последов разбиений, при котор((((( ![]() ))))и при этом n→∞
))))и при этом n→∞
Опред.: если при любых разбиениях отрезка [a;b] : (((((()))))) и при любом выборе точке Сi интегральная сумма 6.1.1 стремиться к одному и тому же пределу S:
![]()
То этот предел
назыв. определ. интегралом от ф-ии f(x)
на отр [a;b]
и обозначается ![]()
Числа a и b соответств. назыв. нижним и верхним пределами интегрирования
Отрезок [a;b] называв.отрезком интегрирования; х-переменная интегриров-я
По определению:
![]() (6.1.2)
(6.1.2)
Опред.: если предел для 6.1.2 существ, то ф-ю называют ИНТЕГРИРУЕМОЙ на отрезке [a;b]
Геометрич-ки опред. Интеграл
От ф-ии f(x) при a<b и f(x)>=0 равен площади криволинейной трапеции ограниченной графиком ф-ии y=f(x), осью OX и прямыми х=а и х=b
![]()
Пример:![]()
ТЕОРЕМА СУЩЕСТВОВАНИЯ
Т.1 если ф-я y=f(x) непрерывна на отр. [a;b] то она интегрируема на этих отрезках
Y=f(x)€C[a;b]
=> &&&
![]()
Т.2 если ф-я y=f(x) ограничена на отр [a;b] и непрерывна на этом отрез. Всюду за искл. Конечного числа точки разрыва, то она интегрир. на этом отрезке.
Привер: ф-я Дирихле
![]()
Ф-я на отр [0;1] неинтегрируема
6.2 Свойства определен. Интегр.
1. a=b
=>![]()
2. a<b
????
![]() => ????
=> ????
![]() и
и ![]()
3. Свойство аддитвности
![]() =>
=>![]()
4. ![]() =>
=>
![]()
5. определ. интеграл от алгебраич суммы нескольких ф-й равен алгебраич .сумме интеграл-ов от слагаемых
![]() =>
=>
![]()
Свойства 4 и 5 назыв. Линейными свойствами опред интеграла
6. f(x)>=0
![]() =>
=>
![]()
7. если ![]() выполняется f(x)<=g(x),
f(x)
выполняется f(x)<=g(x),
f(x)![]() и g(x)
и g(x)![]() =>
=> ![]()
Свойство монотонности
8. если m
и M
наименьш. И наиб. Знач ф-ии f(x)
на отр [a,b],
где a<=b
и ![]() =>
справедливо равенство:
=>
справедливо равенство: ![]()
Доказательство:
![]() =>(по
свойст 7)=
=>(по
свойст 7)=![]() =>
=>
(по свойст 4)=> ![]()
Геометрический смысл доказанных неравенств.

Если f(x)>=0,то S кривол.трак. то SaA1B1b =<SaABb=<SAA2B2b
9. если существует
интеграл ![]() и
выполнятся неравенство:
и
выполнятся неравенство:
![]() Модуль интеграла не превосходит интеграла
модуля
Док-во:
Модуль интеграла не превосходит интеграла
модуля
Док-во: ![]() справедливо соотношение
справедливо соотношение ![]()
если а) f(x)>0 б)f(x)<0 по свойст. 7 получим:
=>![]() (
(![]()
![]() )
=>
)
=>
=>![]()
10. если сущ.интегр.
![]() (проверь
так ли, у оли не понятно),
и
для всех х
(проверь
так ли, у оли не понятно),
и
для всех х![]() [a,b],
[a,b],![]() ,
k-const
, a<b
,
k-const
, a<b
![]()
![]() и
и ![]()
Это сво-во следует из сво-ва 9 с учетом сво-ва 4 и 7 .
11. Т.о среднем
Если ф-ия y=f(x) непрерывна на отр. [a,b] тогда на этом отрезке найдется точка С: выполняется равенство:

Док-во:
Из св-ва 8 =>
m(b-a)![]() => m
=> m![]() =>
=>
![]()
причем ![]()
по усл. f(x)
неприрыв. ф-ия и обязательно принимает
хотя бы 1 раз значение зключительное
между m
и M
=> C
![]() [a,b]
,
[a,b]
, ![]() =>
(((((((()))))))))
=>
(((((((()))))))))
![]() =>
=>
![]() -
формула среднего значения а f(c)-среднее
знач. Ф-ии на отр. [a,b]
-
формула среднего значения а f(c)-среднее
знач. Ф-ии на отр. [a,b]
Геометрич. Смысл:
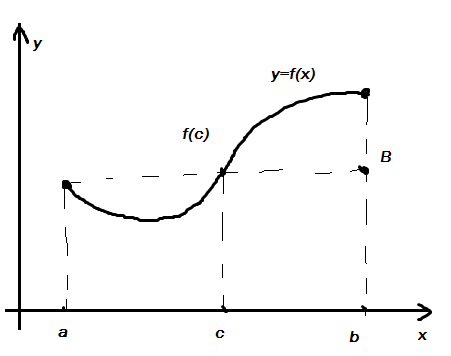
Площадь ограниченная криволин-й трапецией, осью ОХ, прямыми х=а, х=b площадь равнове???????? Площади прямоугольн. Высотой f(c) и основанием длиной (b-a)
12. Определенный интеграл зависит только от подъинтегральной функции f(x) и отрезка интегрирования [a;b] и не зависит от переменной интегрирования, которую можно обозначать любой буквой.
Определенный интеграл по симметричному отрезку.
13. Если f(x) – четная функция
f(-x)=f(x)
![]() из этого следует что
из этого следует что
![]()
14. Если f(x) – нечетная функция
f(-x)=-f(x)
![]() из этого следует что
из этого следует что
![]()
Свойства 13, 14 будут доказаны, когда будет «замена переменной в определенном интеграле».
6.3 Производная от интеграла по его верхнему пределу.
Теорема Барроу.
Пусть в определенном интеграле нижний предел постоянный, а верхний изменяется, тогда будет изменяться значение интеграла, т.е. при рассмотренном условии интеграл есть функция своего верхнего предела.
![]()

![]()
При постоянной а, этот интеграл будет собой представлять функцию верхнего предела
![]()
Теорема Барроу: Если f(x)
– непрерывная функция на [a;b]
и
![]() - функция верхнего предела, то тогда от
x
- функция верхнего предела, то тогда от
x
![]() {производная от функции верхнего предела
равна подынтегральной функции}.
{производная от функции верхнего предела
равна подынтегральной функции}.
Доказательство: Пусть
![]() -приращение
аргумента
-приращение
аргумента
![]() ,тогда
приращение функции Ф(х) будет равно:
,тогда
приращение функции Ф(х) будет равно:
![]() {по
условию}=
{по
условию}=![]() {для
первого слагаемого в алгебраической
сумме применим св-во 3}=
{для
первого слагаемого в алгебраической
сумме применим св-во 3}=![]() {св-во
11(т. О среднем)}=
{св-во
11(т. О среднем)}=![]()
![]() {с
учетом
{с
учетом
![]() }=
}=![]() {по условию f(x)
– непрерывная функция}.
{по условию f(x)
– непрерывная функция}.
Из теоремы Барроу следует что
![]()
![]()
6.4 Формула Ньютона – Лейбница
Теорема: Если
![]()
Если F(х) – есть какая-либо первообразная от функции f(х), которая непрерывна на [a,b], тогда справедлива формула Н.-Л.
Доказательство: Пусть F(x)
– некоторая первообразная от функции
f(x), то по
теореме Барроу
![]()
Две любые первообразные от данной функции отличаются на постоянное слагаемое – С.
![]()
![]()
![]()
![]()
Воспользуемся
![]() {
{![]() знак
двойной подстановки}
знак
двойной подстановки}
По св-ву 12 (![]() )
и получим формулу Н. – Л.
)
и получим формулу Н. – Л.
![]()
Вывод: формула Н.- Л. позволяет вычислить определенный интеграл в том случае, когда известна первообразная подынтегральной функции.
Примеры:
1)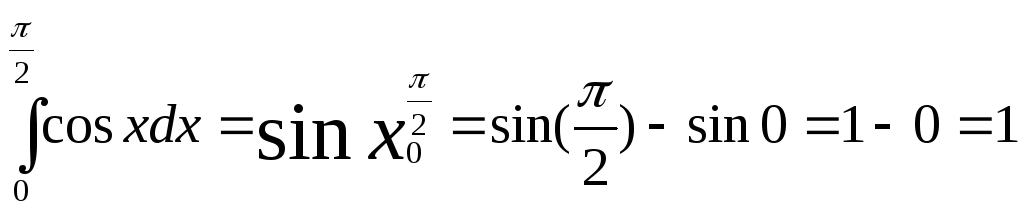
2)Вычислить среднее значение функции: f(x)=x на отрезке [0,n/2]

6.5 Замена переменной в определенном интеграле
Пусть функция y=f(x) определена и непрерывна на отрезке [a,b], t - новая переменная, такая что x=g(t).
Пусть функция g(t)
– непрерывна на отрезке [![]() ],
имеет
],
имеет
1)
![]() -
непрерывную производную на этом отрезке.
-
непрерывную производную на этом отрезке.
2)![]()
3)![]() тогда
справедлива формула замены переменой
в определенном интеграле.
тогда
справедлива формула замены переменой
в определенном интеграле.
![]() 6.5.1
6.5.1
Доказательство: Пусть F(x) первообразная для f(x) по определению первообр.

Интегрируя оба равенства в пределах от a до b получаем
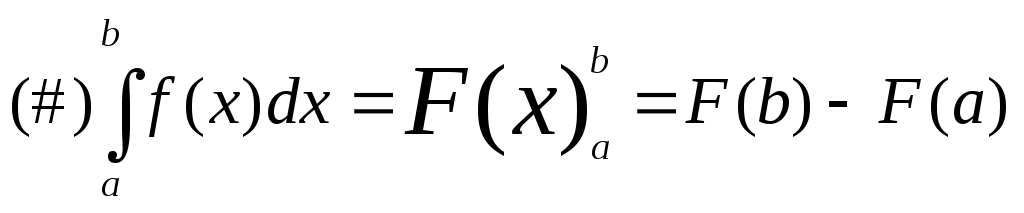 по формуле Н. – Л.
по формуле Н. – Л.
![]()
По условию 2 теоремы: Правые части последующих выражений равны, то равны и левые—что и доп. формулу замены переменной в определенном интеграле.
Замечание: при вычислении определенного интеграла по 6.5.1 к старой переменной не возвращаемся.
Примеры:
1)
=![]()
2) Формула дл интеграла по симметричному отрезку от -а до а
![]() =
=
![]()

![]() четная
функция
четная
функция
![]() нечетная
функция
нечетная
функция
3)![]()
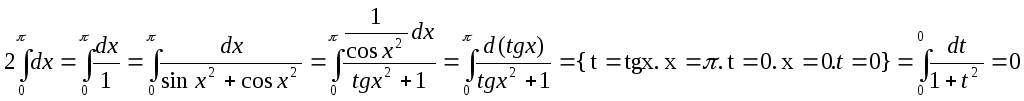
6.6 Интегрирование по частям в определенном интеграле.
Пусть U(x),
V(x)
![]()
Докажем формулу интегрирования по частям в определенном интеграле
![]()
![]() -
формула интегрирования по частям.
-
формула интегрирования по частям.
![]()
Пример:
![]()
=![]()
6.7 Несобственные интегралы
В определенном интеграле
![]()
1)[a,b]
2)
![]()
Возникает необходимость распространить определенный интеграл на случай:
1)бесконечного промежутка интегрирования
2)разрывной подынтегральной функции
Признаки сходимости несобст-ых Интег-ов с бесконечн. Предел.
Т.1 Если для ![]() x
x![]()
![]() ;
;
Т.2 Для случая ф-ии ![]() х
х![]() выполняется неравенство 0
выполняется неравенство 0![]()
![]() и
и
![]() -расходятся.
-расходятся.
Т.3 для случая ф-ия f(x) имеющий знак в бесконечном промежутке,
Если ![]() dx
dx![]() ,
, ![]() этот
этот
![]() абсолютно
сходящийся .
абсолютно
сходящийся .
6.7.2 ![]() от
неограниченных ф-ий. Несобственный
от
неограниченных ф-ий. Несобственный
![]() 2-го
рода.
2-го
рода.
Сущ-ет у=f(x) определена и непрерывна для всех х принадлежащих на [a,b) в (.) х=b либо определена, либо имеет бесконечный разрыв.
Определение ![]() ф-ии f(x) в
(.) по определению равен:
ф-ии f(x) в
(.) по определению равен:
![]() (6.7.2.1)
(6.7.2.1)
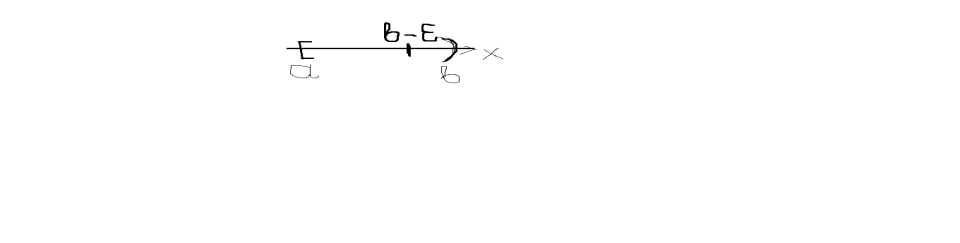
Если предел в правой части сущ-ет и
конечен, то несобственный ![]() наз-ся Сходящимся, в противном случае
(предел не сущ-ет или =
наз-ся Сходящимся, в противном случае
(предел не сущ-ет или =![]() ,
, ![]() наз-ся Расходящимся.
наз-ся Расходящимся.
Пусть ф-ия у=f(х) не прерывна
на ![]() [a,b] в (.) х=с
ф-ия или неопределенно либо имеет
бесконечн разрыв , то по определению
[a,b] в (.) х=с
ф-ия или неопределенно либо имеет
бесконечн разрыв , то по определению![]() ,
,![]() , то ,
, то ,
![]() (6.7.2.2)
(6.7.2.2)

Если предел в правой части сущ-ет и конечен , то Интег-ал назыв-ся Сходящимся, в противном случае Расходящимся!
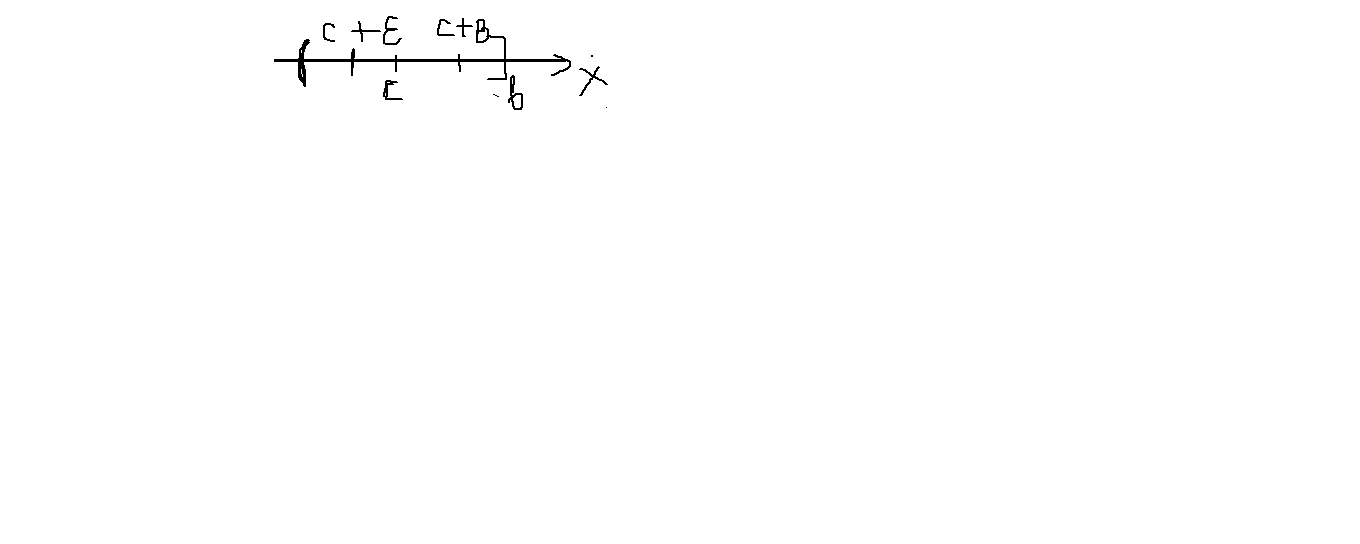
Если ф-ия у=f(x)
имеет бесконечный разрыв в (.) х=с или
неопределена, где а![]() с
с![]() b
, тогда
b
, тогда
![]() (6.7.2.30)
(6.7.2.30)
Если сходится одновременно оба Интег-ла в Прав. Части , то сходится Интег-л и в левой части. Если хотя бы один из Интег-лов в Прав-й части расходится, то расходится и Интег-л в левой части.

Если функция у=f(x)
на отрезке [a,b],
где она определена и непрерывна, и имеет
конечное число (.) разрыва ![]()
![]() тогда
несобственный Интеграл определяется
следующим образом:
тогда
несобственный Интеграл определяется
следующим образом: ![]()
Если каждый из несобственных ![]() в
правой части равенства сходится, то
сходятся
в
правой части равенства сходится, то
сходятся ![]() в левой части, если хотя бы один из них
расходится, то расходится и исходный
в левой части, если хотя бы один из них
расходится, то расходится и исходный
![]() .
.
Признаки сходимости несобственных
![]() от
разрывных фун-ий.
от
разрывных фун-ий.
Т.1 Если на промежутке [a,b)
ф-я у=f(x) и
g(x) определены
и непрерывны в (.) x=b
эти ф=ии имеют разрыв для всех ![]()
![]() ,
, ![]()
И з
геометрич. смысла определённого интеграла
для областей задаваемых соотношениями
a
з
геометрич. смысла определённого интеграла
для областей задаваемых соотношениями
a![]() x
x
![]() b,
y1(x)
b,
y1(x)![]() y
y![]() y2(x)
справедлива формула для вычисления S
области , ограниченной графиками ф-ий
y1(x),
y2(x)
и прямыми x=a,
x=b.
y2(x)
справедлива формула для вычисления S
области , ограниченной графиками ф-ий
y1(x),
y2(x)
и прямыми x=a,
x=b.
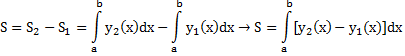
Е сли
область задана с соотношениями c
сли
область задана с соотношениями c![]() y
y![]() d
, g1(y)
d
, g1(y)![]() x
x![]() g2(y),
то
g2(y),
то
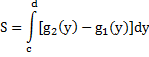
Если прямая линия
задана параметрически ![]() ,x(t),
y(t)
,x(t),
y(t)
![]() ,
непрерывн. диф. на отрезке
,
непрерывн. диф. на отрезке ![]() .
x(
.
x(![]() =a;
x(
=a;
x(![]() )=b
)=b