
6.9 Вычисление площади плоской фигуры в полярной системе координат.
Пусть линия огранич. плоскую фигуру задана в полярной системе координат.
Пример: Вычислить длину окружности: x2+y2=R2
Вычислить длину 4-ой части окружности, расположенной в I квадранте(х≥0, y≥0):


Если
уравнение кривой задано в параметр-ой
форме:
 , функции x(t),
y(t) определены
и непрерывны вместе со своими производными
на отрезке [α,β]. Производная
, функции x(t),
y(t) определены
и непрерывны вместе со своими производными
на отрезке [α,β]. Производная
![]() ,
тогда сделав подстановку
,
тогда сделав подстановку
![]() в
формулу:
в
формулу:
![]() и учитывая что
и учитывая что
![]()
получим
 внесем множитель
внесем множитель
![]() под
знак корня и получим окончательно
под
знак корня и получим окончательно
![]()
Замечание:
Задана плоская кривая , можно также
рассматривать функцию, заданную
параметр-ки в пространстве, тогда
добавится функция z=z(t)
и формула
![]()
Пример: Вычислить длину астроиды, которая задаётся уравнением: x=a*cos3(t), y=a*sin3(t), a>0

Вычислить длину 4-ой части:
![]() по
формуле
по
формуле![]()
 Длина
дуги плоской кривой, заданной в полярной
системе координат:
Длина
дуги плоской кривой, заданной в полярной
системе координат:
Пусть
в полярной системе координат задано
уравнение кривой:
![]() -
непрерывная функция, вместе со своей
производной на отрезке [α,β].
-
непрерывная функция, вместе со своей
производной на отрезке [α,β].
Формулы перехода от полярных координат:
рассматривать как параметрические:
![]()
ϕ -
параметр, по ф-ле
![]()
2
Пр:
Вычислить длину кривой :
![]() >0
>0


З -ние: вычислим половину длины окружности:
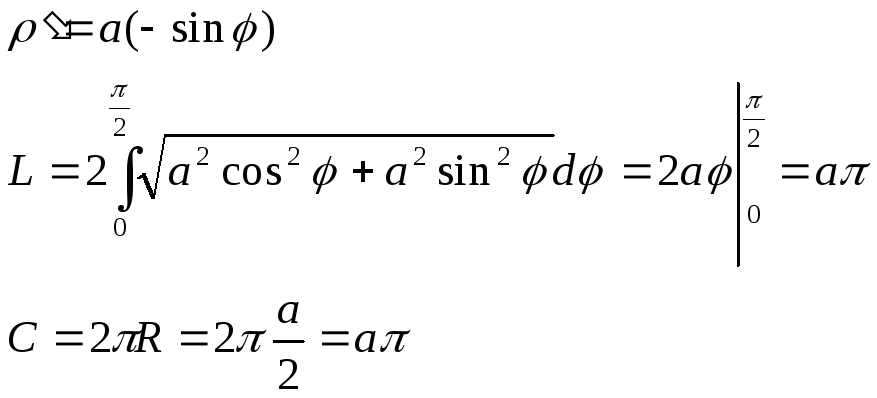
Объём тела, вычисляемый по площади поперечного сечения тела.
Пусть задано тело, ограниченное замкнутой поверхностью и пусть известна площадь любого сечения этого тела плоскостью, перпендикулярной к оси Ох. Эта площадь будет зависеть от положения секущей плоскости.
![]() пусть
все тело заключено между 2-мя
перпендикулярными к оси Ох плоскостями,
пересекающими её в точках х=а, х=b
(a<b)
пусть
все тело заключено между 2-мя
перпендикулярными к оси Ох плоскостями,
пересекающими её в точках х=а, х=b
(a<b)

Для
определения объёма такого тела разобьём
его на слои с помощью секущих плоскостей,
перпендикулярных к оси Ох и пересекающих
её в точках
![]() .
В каждом частичном промежутке
.
В каждом частичном промежутке
![]() .
Выберем
.
Выберем
![]() и для каждого значения i=1,….,n
построим цилиндрическое тело, образующая
которого параллельна Ох, а направляющая
представляет собой контур сечения тела
плоскостью х=Сi ,
объем такого элементарного цилиндра с
площадью основания S=Ci
и высотой ∆хi .
Vi=S(Ci)∆xi
. Объём всех таких элементарных цилиндров
будет
и для каждого значения i=1,….,n
построим цилиндрическое тело, образующая
которого параллельна Ох, а направляющая
представляет собой контур сечения тела
плоскостью х=Сi ,
объем такого элементарного цилиндра с
площадью основания S=Ci
и высотой ∆хi .
Vi=S(Ci)∆xi
. Объём всех таких элементарных цилиндров
будет
![]() .
Предел этой суммы, если он существует
и конечен при max ∆х
0 называется объёмом данного тела.
.
Предел этой суммы, если он существует
и конечен при max ∆х
0 называется объёмом данного тела.
 .
Так как Vn
интегральная сумма для непрерывной на
отрезке [a,b]
функции S(x)
то указанный предел существует (т-ма
существования) и выражается опр.
Интегралом.
.
Так как Vn
интегральная сумма для непрерывной на
отрезке [a,b]
функции S(x)
то указанный предел существует (т-ма
существования) и выражается опр.
Интегралом.
![]() - объём тела, вычисляемый по площади
поперечного сечения.
- объём тела, вычисляемый по площади
поперечного сечения.
Объём тела вращения:
Пусть тело образовано вращением вокруг оси Ох криволинейной трапеции, ограниченной графиком функции y=f(x), осью Ох и прямыми x=a, x=b.

Пусть
функция y=f(x)
определена и непрерывна на отрезке
[a,b] и
неотрицательна на нем, тогда сечение
этого тела плоскостью, перпендикулярной
Ох есть круг, радиусом R=y(x)=f(x)
. Площадью круга S(x)=Пy2(x)=П[f(x)]2.Подставляя
формулу
![]() получим формулу для вычисления объёма
тела вращения вокруг оси Ох:
получим формулу для вычисления объёма
тела вращения вокруг оси Ох:
![]()
Если
же вокруг оси Оу вращается криволинейная
трапеция, ограниченная графиком
непрерывной на [c,d]
функцией
![]() ,
то объём такого тела вращения:
,
то объём такого тела вращения:

![]()
Этот
же объём может быть вычислен по формуле:
![]() .
Если линия задана параметрическими
уравнениями :
.
Если линия задана параметрическими
уравнениями :
Делая замену переменной получим:
![]()
Если
линия задана параметрическими уравнениями
:
y(α)=c, y(β)=d. Делая замену y=y(t) получим:
![]()
Вычислить ![]() тела
вращения вокруг оси ОУ параболы
тела
вращения вокруг оси ОУ параболы ![]() ,
,![]()
![]() .
.
1способ:


2способ:


2)Вычислить V тела вращения
вокруг оси ОХ криволинейной трапеции,
ограниченной прямой у=0, дугой ![]() ( с центом в точке(1;0), и радиусом=1), при
( с центом в точке(1;0), и радиусом=1), при
![]() .
.

Площадь поверхности тела вращения
Пусть заданна поверхность образованная
вращением кривой у =f(х)вокруг
оси Ох. Необходимо определить S
этой поверхности при ![]() .
.
Пусть функция у =f(х) определенна и непрерывна, имеет неприр.и неотрицательна во всех точках отрезка [а;в]
Проведем хорды длины которых обозначим соответственно (n-хорд)
![]()

по теореме Лагранжа:
![]()
Тогда:
![]()
Площадь поверхности всей описанной ломанной будет равна
![]()
Определение: предел этой суммы, если он
![]() и конечен, когда наибольшее звено ломаной
max
и конечен, когда наибольшее звено ломаной
max![]() ,
, ![]() называется площадью рассматриваемой
поверхности вращения.
называется площадью рассматриваемой
поверхности вращения.
Можно доказать, сто предел суммы равен
приделу интегрированной суммы для р-ий
![]()

![]() формула для S поверхности
тела вращения =
формула для S поверхности
тела вращения = ![]()
S поверхности образованной
Вращением дуги кривой х=g(x)
вокруг оси Оу при![]()
Непрерывна со своей производной ![]()

Если кривая заданна параметрически
ур-ми x=x(t) , y=t(t)
![]() ф-ии x’(t),
y’(t),x(t),y(t)
определенны на отрезке [a;b],x(a)=a,
x(b)=b
то сделав замену переменой x=x(t)
ф-ии x’(t),
y’(t),x(t),y(t)
определенны на отрезке [a;b],x(a)=a,
x(b)=b
то сделав замену переменой x=x(t)

Если кривая заданна параметрически сделав замену в формуле получим:

Если уравнение кривой заданно в
полярной системе координат ![]()
S поверхности вращения
вокруг оси будет равно

