3.6.3.Ячеечная модель

Передаточная функция ячеечной модели имеет следующий вид:

(3.6.23)

После дифференцирования и нахождения пределов производных, можно найти следующие соотношения между моментами кривой распределения и параметрами модели:

(3.6.24)

Из выражения для дисперсии видно, что при n дисперсия ²0. Это свидетельствует о том, что ячеечная модель при этом стремится к модели идеального вытеснения. Третий центральный момент является величиной положительной, следовательно функция распределения будет иметь правостороннюю асимметрию

(затянутый переходный процесс). На основании полученных формул для М₁ и М₂ обычно рассчитывают параметры модели (иn) а третий момент используют для проверки адекватности модели.

3.6.4.Диффузионная однопараметрическая модель

Передаточная функция для аппарата больших размеров, описываемого диффузионной моделью имеет вид:

(3.6.25)

После дифференцирования передаточной функции и выражения моментов кривой распределения через соответствующие производные получим следующие уравнения связи:

(3.6.26)

Сопоставим значения второго момента для диффузионной и ячеечной модели:

Из предыдущего выражения, разрешая его относительно М₂, получим:

(3.6.27)

Критерий Пекле равен удвоенному числу ячеек.

С помощью такой процедуры можно получить уравнения связи моментов кривых распределения с параметрами для любых моделей, включая комбинированные. Однако для сложных комбинированных моделей уравнения связи не всегда могут быть выражены в явном виде через моменты кривых распределения.

3.6.5.Вычисление моментов по экспериментальным данным.

Экспериментальная С(t) кривая получается при подаче на вход аппарата импульсного возмущения в виде -функции и представляет собой изменение концентрации трассера во времени (рис. 3.6.1)

Рис.3.6.1. Экспериментальная С_э(t) кривая . S_o площадь, ограниченная кривой и осью абсцисс

Для того, чтобы воспользоваться приведенными выше формулами , необходимо найти соответствие между теоретической С(t) кривой и экспериментальной кривой. Это соответствие устанавливается введением масштабного множителя М таким образом, чтобы выполнялось условие нормировки: т.е.

(3.6.28)

где М₀ начальный момент нулевого порядка. Отсюда находим:

(3.6.29)

Таким образом, масштабный множитель М есть площадь, ограниченная С_э(t) –и осью абсцисс, т.е. S₀.

Учитывая полученные выражения, можем записать формулы для расчета моментов по экспериментальной С_э(t) – кривой. Для начального момента 1-го порядка получим выражение:

(3.6.30)

Для момента любого порядка можно записать:

(3.6.31)

Для нахождения численного значения определенных интегралов используют два метода аппроксимации интегралов – ступенчатый, когда площадь под кривой аппроксимируется суммой площадей прямоугольников (см. рис.3.6.2),

Рис…3.6.2. Метод ступенчатой аппроксимации площади.

или кусочно-линейной аппроксимации, когда площадь под кривой

аппроксимируется суммой площадей соответствующих трапеций, вписанных под кривой (рис.3.6.3).

Рис.3.6.3. Метод линейно - кусочной аппроксимации интеграла

При использовании ступенчатой аппроксимации площадь под кривой вычисляется следующим образом:

(3.6.32)

где n – число интервалов t. Для начального момента 1-го порядка формула принимает вид:

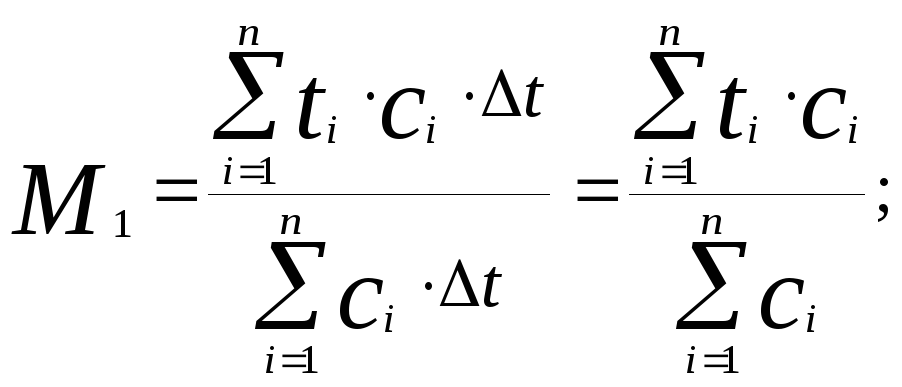(3.6.33)

Для момента порядка s получим выражение:

(3.6.34)

При ступенчатой аппроксимации С_э(t) ошибка нарастает по мере возрастания порядка момента, особенно для несимметричных кривых, как это видно из Рис. 3.6.2. Для увеличения точности вычислений применяют кусочно-линейную аппроксимацию, как это показано на Рис.3.6.3. При этом суммарная площадь вычисляется как сумма площадей трапеций, вписанных под экспериментальной С_э(t) кривой. В этом случае начальный момент нулевого порядка может быть вычислен по формуле:

(3.6.35)

Для нахождения начального момента порядка s воспользуемся соотношением:

(3.6.36)

Тогда для начального момента порядка s получается соотношение:

(3.6.37)

Из полученной общей формулы найдем для момента первого порядка выражение:

; (3.6.38)

После аналогичных преобразований, учитывая формулу для разности кубов, найдем выражение для второго начального момента С(t) –кривой:

(3.6.39)

Таким образом, используя полученные соотношения можно по экспериментально полученным С_э(t) – кривым рассчитать начальные моменты функции распределения, а по ним рассчитать параметры моделей потоков, описывающих перенос вещества движущейся средой в данном аппарате.

С помощью описанной методики были определены параметры моделей потоков для многих аппаратов. Эти результаты были обобщены в виде критериальных уравнений. Например, для течения в круглых трубах в ламинарном режиме была получена следующая обобщающая зависимость:

(3.6.40)

Для течения в трубе при турбулентном режиме зависимость имеет следующий вид:

(3.6.41)

где  - коэффициент трения, зависящий от числа Re и от шероховатости внутренней поверхности трубопровода.

Однако описанная методика определения параметров моделей по экспериментальным кривым отклика, хотя и является общепринятой, имеет некоторые принципиальные недостатки:

1. Связь моментов кривой распределения с производными от передаточной функции получена в предположении, что входной возмущающий сигнал подается в форме единичного импульса, или -функции. На практике такой входной сигнал реализовать невозможно, а, следовательно, необходимо производить дифференцирование передаточной функции с учетом реального входного сигнала. Это приводит к большим математическим трудностям.

2. Выходная функция C_э(t) должна измеряться и интегрироваться при t, так как только при этом условии выполняется предел производной передаточной функции р0 и имеют место полученные уравнения связи между моментами кривой распределения и параметрами гидродинамических моделей. Это условие также трудно реализовать экспериментально, поскольку эксперимент всегда проходит за конечное время, и малые количества трассера трудно регестрировать экспериментально.

Поэтому в последнее время получил распространение другой подход к определению параметров моделей структуры потоков по экспериментальным данным, основанный на общем подходе к задаче идентификации математических моделей на основе методов нелинейного программирования.