Лекция 3

СИМПЛЕКС-МЕТОД РЕШЕНИЯ ЗАДАЧ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ

УЧЕБНЫЕВОПРОСЫ:

1.Задача о распределении ресурсов.

2.Каноническийвид задачи линейного программирования.

3.Алгоритм симплекс-метода.

4.Алгоритм симплекс-методас искусственным базисом.

1

ЗАДАЧА ОБ ИСПОЛЬЗОВАНИИ РЕСУРСОВ (ПЛАНИРОВАНИЯ ПРОИЗВОДСТВА)

Для изготовления двух видов продукцииP1 и P2 используют 4 вида ресурсов:S1, S2, S3 и S4. Запасы ресурсов, затратыресурсов на производствокаждоговида продукции

		Запас	Количестворесурсов на
	Вид ресурса		одну единицупродукции
		ресурса
			P1	P2
	S1	18	1	3
	S2	16	2	1
	S3	5	-	1
	S4	21	3	-

Прибыльот производстваединицы продукции P1 и P2 равны, соответственно,2 и 3 руб.

Необходимосоставитьтакой план производствапродукции, при

которомприбыль от реализации ее будет максимальной.

2

ФОРМАЛИЗОВАННОЕ ОПИСАНИЕ ЗАДАЧИ:

Целевая функция:

…Прибыль от производства единицы продукции P1 и P2 равны, соответственно, 2 и 3 руб. … и должна стремиться к максимуму.

План производства– количество единиц продукции P1 и P2 , которыеобозначим x1 и x2. С учетомцены с1 = 2 и с2 = 3, целевая функция приметследующий вид: F 2 x1 3 x2 max

Неравенства составляются по каждомуресурсу с подстановкойпланируемого количества производстваизделий каждоготипа:

Не указанные явно в условии задачи, но очевидныеусловия на неотрицательность количестваизделий каждоготипа:

x1 3 x2 18

2 x1 x2 16x2 5

3 x1 21

x1 0	x2 0
	3

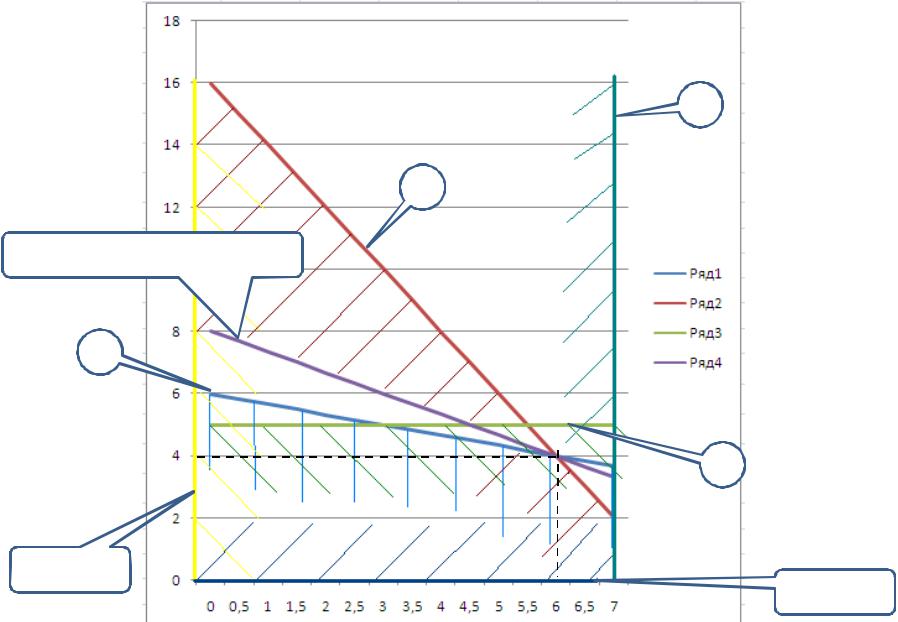
ГРАФИЧЕСКОЕ РЕШЕНИЕЗАДАЧИ ОБ

ИСПОЛЬЗОВАНИИ РЕСУРСОВ

4

2

F 2 x	3 x	2	max	x1	3 x2	18
1						16
				2 x1 x2
1				x2	5

3 x1 21

3

x2 0

x1 0 4

ЗАДАЧИ ОБ ИСПОЛЬЗОВАНИИ РЕСУРСОВ В ОБЩЕМ ВИДЕ:

Найти план выпуска n видовпродукции с использованием m видовресурсов. где: xj (j=1..n) – число единиц продукции каждого типа,запланированного к производству.

bi (i=1..m) – запас каждоговида ресурса;

aij – число единиц ресурса Si, затрачиваемогона изготовление единицы продукции Pj (технологическиекоэффициенты);

cj – прибыль отреализации единицы продукции вида Pj, удовлетворяющийусловиям:

прикоторомцелевая функция принимаетмаксимальное значение:

a11x1 a12x2 ...						a1nxn b1
						a2nxn b2
a21x1 a22x2
............................................
a	x a	m2	x	2	...	a	mn	x	n	b
	m1 1									m

x1 0 x2 0

xn 0

F c1x1 c2x2 ... cnxn max

5

КАНОНИЧЕСКИЙ ВИД ЗАДАЧИ ЛП

Fc1x1 c2x2 cnxn max

a11 x1 a12 x2 a1n xn b1

	a21 x1 a22 x2 a2n xn b2
	am1 x1 am2 x2 amn xn bm

xj 0,

j 1,2...n

1. Если исходная задача былазадачей на минимум, товведением новойцелевой функции

F1 =-F

мы преобразуем нашу задачуна минимум функции Fв задачу на максимум функции F1.

2. Если в исходной задаче некотораяпеременная не подчинена условию неотрицательности, тоее заменяют (в целевой функции и вовсех ограничениях) разностью неотрицательных переменных

где: Xk>=0,Xl>=0	Xk=Xk-Xl
l - свободный индекс	6

КАНОНИЧЕСКИЙ ВИД ЗАДАЧИ ЛП

3. Еслив исходнойзадаче некотороеограничение(например,первое) былонеравенством,то онопреобразуетсяв равенство,введением в

левуючасть некоторойнеотрицательнойпеременной, причем в неравенства«≤» вводитсядополнительнаянеотрицательнаяпеременная сознаком«+»; в случаи неравенства«≥» - со знаком«-»:

a11x1+a12x2+...+a1nxn<=b1

Вводимпеременную:

xn+1=b1-a11x1-a12x2+...+a1nxn.

Тогданеравенствозапишетсяв виде:

a11x1+a12x2+...+a1nxn+xn+1=b1

В каждоеиз неравенстввводитсясвоя"уравнивающая”переменная, послечего системаограниченийстановитсясистемойуравнений.

4. Еслив ограниченияхправаячасть отрицательна,тоследуетумножить этоограничениена (-1)

Таким образом,всякую задачу линейного программирования

можносформулироватьв канонической форме.

7

АЛГОРИТМ СИМПЛЕКС-МЕТОДА

1.	Способопределенияпервоначального	x1 3 x2			x3	18
	допустимогобазисногорешения.
				x2	x4	16
2.	Правилопереходак лучшему (не худшему)	2 x1
	решению.	x	x 5
3.	Критерийпроверкиоптимальности	2		5
	найденногорешения.			x6	21
		3 x1

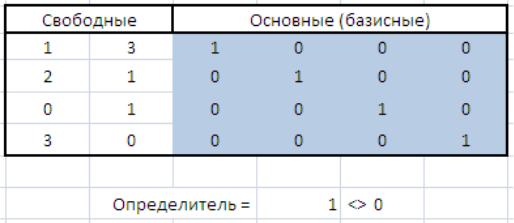
Любые m переменных системыm линейныхуравненийс nпеременными (m< n) называютсяосновными (базисными) еслиопределитель матрицы коэффициентовпри них отличенот нуля.

Тогдаостальныеn– m переменных называютсянеосновными (свободными).

Основнымимогутбыть разные группы из n переменных.

8

Полагаем неосновные переменные (x1 и x2) равными 0, получаем базисное решение: X1 = (0, 0, 18, 16, 5, 21),

которое является допустимым и соответствует вершине 0, 0 области допустимых решений

9

ТЕОРЕМА О РАЗРЕШИМОСТИ ЗАДАЧИ ЛП

Если для системы m линейных уравнений с n переменными (m < n) ранг матрицы коэффициентов при переменных равен m, т.е. существуетхотя бы одна группа основных переменных , тоэта система называетсянеопределенной, причем каждому произвольномунабору значений неосновных переменных соответствуетодно решение системы.

Базиснымрешением системы m линейных уравнений с n переменными называется решение, в которомвсе n-m неосновных переменных равны нулю. Число базисных решений являетсяконечным,т.к. оно равно числу групп основных переменных, не превосходящее Cnm

10