И.Ф. Шишкин. ТЕОРЕТИЧЕСКАЯ МЕТРОЛОГИЯ

________________________________________________________________

4.5. МАТЕМАТИЧЕСКИЕ ДЕЙСТВИЯ С РЕЗУЛЬТАТАМИ ИЗМЕРЕНИЙ

4.5.1. Математические действия с одним результатом измерения

При математических действиях над результатами измерений нужно учитывать, что последние являются случайными значениями измеренных величин. Обращение с

результатами измерений как с неслучайными значениями приводит к ошибкам.

Некоторые из них будут рассмотрены на конкретных примерах.

Начнем с умножения результата измерения на постоянный множитель.

Пример 39. Удвоить результат измерения r, эмпирическое распределение вероятности числового значения которого представлено табл. 10.

		Таблица 10
	r	m		Р
	3	20		0,2
	4	50		0,5
	5	30		0,3
Решение.	Результатом умножения случайного числа r на 2 будет новое случайное число 2r,
распределение вероятности которого:		2r	P
		6	0,2
		8	0,5
		10	0,3
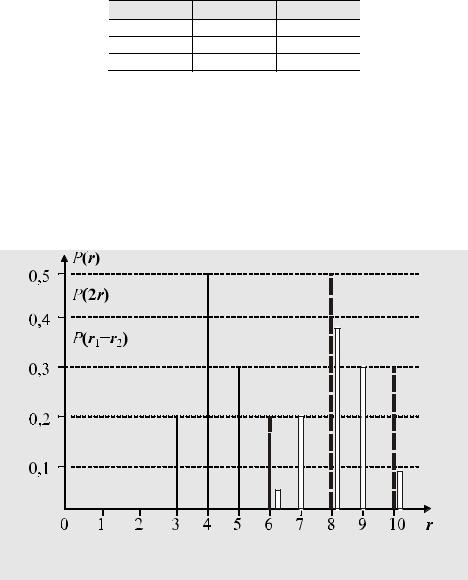
Графически оно показано на рис. 36. Вероятность			удвоенных	по сравнению с r значений остается
прежней.
		Рис. 36.
	Распределение вероятностей P(r), P(2r) и P(r+r) в примерах 39 и 43

76

Часть I. ОБЩАЯ ТЕОРИЯ ИЗМЕРЕНИЙ

___________________________________________________________________________

Оценки числовых характеристик теоретической модели эмпирического распределения вероятности, представленного табл. 10,

ˆ

1

n

3× 20 + 4 ×50 + 5 ×30

r

=

ri

=

= 4,1;

n

100

∑i=1

2

1

n

2

ˆ

2

9×20 +16×50 + 25×30

∑ri

Sr

=

−r

=

16,8

= 0,5 .

n

100

i=1

Оценки числовых характеристик теоретической модели нового случайного числа

		2r		= 8 ; S22r = 2 ,
следовательно,
				ˆ	2	2
2r = 2r ; S2r						= 4Sr .

Таким образом, для оценок справедливы свойства самих числовых характери-

стик (см. п. 4.3.2): среднее арифметическое произведение постоянного множителя а

и результата измерения А равно произведению постоянного множителя и среднего арифметического значения результата измерения, то есть, если

Q = a A ,

то

ˆ = ˆ Q aA.

В равной мере стандартное отклонение произведения постоянного множителя а и результата измерения А равно произведению модуля постоянного множителя и стандартного отклонения результата измерения:

SQ = a SA .

Теперь рассмотрим операцию возведения результата измерения в квадрат. Под квадратом результата измерения А понимается случайная величина

Q = A2 ,

которая с вероятностями Pi , соответствующими значениям Ai , принимает значения, равные Qi .

77

И.Ф. Шишкин. ТЕОРЕТИЧЕСКАЯ МЕТРОЛОГИЯ

________________________________________________________________

Пример 40. Возвести в квадрат результат измерения, рассмотренный в предыдущем примере. Решение. Распределение вероятности числовых значений r2 выглядит следующим образом:

r2	Р
9	0,2
16	0,5
25	0,3

Оценки числовых характеристик теоретической модели этого распределения вероятности

r 2 =17,3 ; Sr2 = 5,7.

Рассмотренные примеры показывают, что при функциональном преобразовании результата измерения

Q = f(A)

(14)

происходит трансформация его эмпирического закона распределения вероятности в соответствии с правилом

P(Qi ) = P(Ai ).

Если результат измерения А задан теоретической моделью эмпирического закона распределения вероятности, то используется то, что интегральная функция распределения вероятности F(Q) представляет собой вероятность того, что

f(A) < Q.

Решение этого неравенства относительно А устанавливает пределы, в которых находится А с вероятностью F(Q). Последняя равна интегралу от плотности вероятности pA

(A) в установленных пределах.

Пример 41. Определить трансформацию плотности вероятности pA (A) результата измерения A после линейного преобразования Q = а А + b.

Решение. 1. F(Q) = P{aA + b < Q}.

2. С вероятностью F(Q) результат измерения

A <	Q − b			при	а > 0;
	a
A >	Q − b			при	а < 0. Отсюда
	a
		Q−b
F(Q)=		∫a pA (A)d A				при	а > 0 ,
		−∞
		∞∫pA (A)d A
F(Q)=						при	а < 0.
	Q−b
		a

78

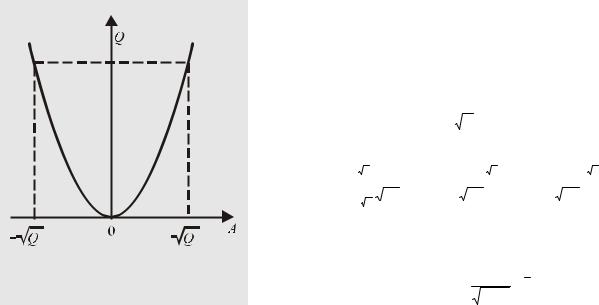
Часть I. ОБЩАЯ ТЕОРИЯ ИЗМЕРЕНИЙ

___________________________________________________________________________

3. После перестановки пределов в последнем интеграле и дифференцирования получаем:

p(Q)=		1			Q − b
				p			.
		a				a
					A

Таким образом, как это можно было заметить еще на примере 39, при линейном преобразовании результата измерения распределение вероятности не меняется, а

происходит только его смещение по оси абсцисс и компрессия либо декомпрессия.

Результат, полученный в примере 41, применительно к любой монотонной функции (14) обобщается следующим образом:

p(Q)=		df −1(Q)		pA [f −1(Q)],
		d Q

	где f -1 — функция, обратная функции f. В примере 41 f −1 =	Q − b	. Если f -1	— много-
		a

значная функция, то это отражается на пределах, в которых находится А с вероятностью F(Q).

Пример 42. Определить трансформацию нормированного нормального закона распределений вероятности, которому подчиняется результат измерения A, после нелинейного преобразования Q = А 2 .

Решение.

Рис.37.

Графическое решение уравнения, обратного возведению A в квадрат

1.F (Q) = Р {А2 < Q}.

2.Пределы, в которых выполняется неравенство,

устанавливаются функцией A = ± Q , обратной возведению A в квадрат (рис. 37). Поэтому

Q

1

e−

A2

1

Q

e−

A2

1

−

Q

A2

F(Q)= ∫

d A =

∫

d A −

∫

e

d A .

2

2

2

2 π

2 π

2 π

− Q

0

0

3. После дифференцирования получаем:

p(Q)= 21πQ e−Q2 .

Для сравнения графики плотности исходного и преобразованного распределения вероятности показаны на рис. 38.

На практике преобразованиями законов распределения вероятности результатов измерений интересуются сравнительно редко. Обычно ограничиваются расчетами на уровне оценок числовых характеристик законов распределений.

79