Часть I. ОБЩАЯ ТЕОРИЯ ИЗМЕРЕНИЙ

________________________________________________________________

где ζ =

1

, в чем нетрудно убедиться, выбрав f (σ

t , σ

t

)= ln

σX t2

= ln

t2

. Не зависящий

1

+ e2ln z

X 1

X

2

σ

X

t

t

1

1

от мощности помех порог обнаружения

zln = ln zп .

7.2. КАЧЕСТВО ИЗМЕРЕНИЙ ПО ГРАДУИРОВАННЫМ ШКАЛАМ

Номенклатура показателей качества при измерении по градуированным шкалам все время претерпевает изменения и окончательно еще не сложилась. Наиболее информативными являются:

-сходимость;

-воспроизводимость;

-неопределенность;

-точность;

-правильность;

-достоверность.

Сходимость

Показатель качества, характеризующий близость результатов измерений одной и той же измеряемой величины, выполненных в одинаковых условиях.

Количественной характеристикой (мерой) сходимости могут быть параметры, характеризующие рассеяние (дисперсию) этих результатов измерений.

Воспроизводимость

Показатель качества, характеризующий близость результатов измерений одной и той же измеряемой величины, выполненных в разных условиях.

Количественной характеристикой (мерой) воспроизводимости могут быть параметры, характеризующие рассеяние (дисперсию) этих результатов измерений.

Неопределенность

Параметр, характеризующий диапазон возможных значений величины.

Количественными характеристиками (мерами) неопределенности могут быть стандартная (определяемая способом А, или способом В), суммарная или расширенная неопределенности.

173

И.Ф. Шишкин. ТЕОРЕТИЧЕСКАЯ МЕТРОЛОГИЯ

________________________________________________________________

Точность

Точность характеризует рассеяние результата измерения

Q = X + θ

около среднего значения, отождествляемого со значением измеряемой величины.

Аддитивная поправка θ является неслучайной величиной, даже если ее значение точно не известно. Поэтому рассеяние результата измерения обусловлено рассеянием показания X , и мерой точности результата измерения служит среднее квадратиче-

ское отклонение показания. На практике вместо него используется оценка среднего квадратического отклонения – стандартное отклонение или стандартная неопределенность показания, определяемая способом А.

Точность многократного измерения с равноточными значениями отсчета в n

раз выше точности однократного (см. формулы (31), (32), где SQ = S X ; S	ˆ	= S	ˆ	). Соот-
	Q		X

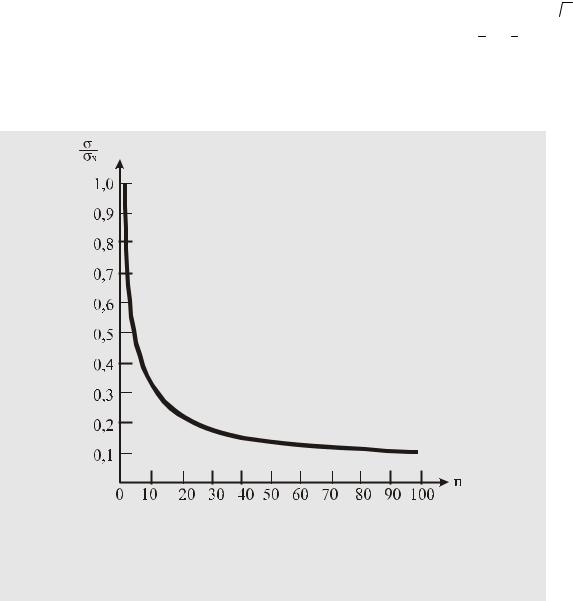
ношение между средними квадратическими отклонениями многократного и однократного измерений в зависимости от объема экспериментальных данных представлено на рис. 80.

Рис. 80.

Соотношение между средними квадратическими отклонениями многократного и однократного измерений

174

Часть I. ОБЩАЯ ТЕОРИЯ ИЗМЕРЕНИЙ

________________________________________________________________

Как следует из графика на рис. 80, увеличивая количество эксперименталь-

ных данных, можно повышать точность результата многократного измерения

вплоть до заданного уровня. Однако, уже при n > 20…30 дальнейшее повышение точности таким путем сопряжено с существенными затратами на выполнение большого количества измерений и малоэффективно.

Другим ограничением на пути повышения точности является правило округлений. Если при многократном измерении с равноточными значениями отсчета во все значения показания вносится одна и та же поправка, точное значение которой неиз-

вестно, то суммарная неопределенность результата многократного измерения

u	ˆ	= u 2ˆ	+ uθ2	,
Q		X

где u ˆ - стандартная неопределенность среднего арифметического значения показания,

X

а uθ - стандартная неопределенность поправки, определяемые способом В. Точность результата многократного измерения имеет смысл повышать путем увеличения количе-

ства экспериментальных данных только до тех пор, пока u	ˆ		1 u	ˆ	. При u	ˆ	≤	1 u	ˆ	пер-
X			3 Q		X			3 Q

вым слагаемым в выражении для суммарной неопределенности результата многократного измерения в соответствии с правилом округления можно уже пренебречь (см. формулу (30).

Повышение точности измерения метрологических характеристик средств измерений рабочими эталонами за счет многократного повторения измерительной процедуры позволяет обеспечить требуемое качество поверочных работ. Если требования к качеству поверки сформулированы в виде заданных значений α и βmax , то может оказаться, что система уравнений (см. п. 5.1)

+ δ

+ δ

−δ

−δ

1

σΞ

−

( −δ)2

−

( +δ)2

2

2

α =1−

+

+

2 σΞ

−e

2 σΞ

;

L

L

2 π

e

σΞ

σΞ

βmax = L σ+Ξδ − L σ−Ξδ

не имеет решения. Тогда следует перейти к многократному измерению метрологической характеристики рабочим эталоном. Совместное решение уравнений

175

И.Ф. Шишкин. ТЕОРЕТИЧЕСКАЯ МЕТРОЛОГИЯ

________________________________________________________________

(

−δ)2

( +δ)2

+δ

+

δ

−δ

−δ

1

σΞ

−

n −

n

2

2

α =1−

+

+

2 σΞ

−e

2 σΞ

;

L

σΞ

n

L

σΞ

n

2 πn

e

+ δ

−δ

βmax = L

σΞ

n

−L

σΞ

n

даст значения δ и n при заданных значениях α и βmax .

Правильность

Внесение в показание поправки направлено на достижение правильности результата измерения. Правильность обеспечивается при совпадении среднего значения результата измерения со значением измеряемой величины. Это возможно только в том случае, когда поправка известна точно. Если же точное значение поправки неизвестно, то это учитывается ее ситуационной моделью. В этом случае внесение в показание поправки осуществляется по правилу сложения случайных величин. Чем точнее значение поправки, тем правильнее результат измерения. Таким образом, правильность результата измерения определяется точностью поправки, а мерой правильности является ана-

лог среднего квадратического отклонения поправки или ее стандартная неопределен-

ность, определяемая способом В. Чем она меньше, тем правильнее результат измерения.

При многократном измерении с равноточными значениями отсчета, выполняемом одним и тем же средством измерений, одним и тем же оператором, в одних и тех же условиях во все случайные значения показания Xi вносится одна и та же поправка θi = θ. Поэтому результат многократного измерения при аддитивной поправке

ˆ

1

n

1

n

1

n

ˆ

∑i=1

∑i=1

∑i=1

Qn =

Qi =

X i +

θi = X n + θ.

n

n

n

Таким образом, если точность многократного измерения с равноточными значениями отсчета повышается в n раз:

S	ˆ	=	S X	,
X n			n

то правильность остается такой же, как при однократном измерении:

uθˆ = uθ .

176

Часть I. ОБЩАЯ ТЕОРИЯ ИЗМЕРЕНИЙ

________________________________________________________________

Повысить правильность результата однократного измерения можно, перейдя к многократному измерению с неравноточными значениями отсчета. В этом случае в Xj –е показание каждого из m средств измерений разной точности будет вноситься своя поправка θj . Каждую θj –ю поправку к случайному Xj –му значению показания можно будет рассматривать тоже как случайную величину и обращаться с ней соответствующим образом. Такой прием отнесения поправок к категории случайных величин называется рандомизацией (от англ. random - случайный). Дальнейшее зависит от характера априорной информации.

Если показатели точности и правильности каждого измерения известны,

т. е. известно среднеквадратическое отклонение показания каждого из средств измерений и пределы, в которых находится поправка к нему, то результат измерения определяется по формуле среднего арифметического взвешенного:

			1		X		+		1				X				+... +			1					X		+		1			θ		+	1		θ	2	+... +			1	θ	m
			σX2			1			σX2							2				σX2						m				uθ2				1	uθ2							uθ2
Q =																								m												2									.
			1						2																						1											m
									1			+				1			+.... +					1		+			1		+			1	+.... +					1
							σX2							σX2				2				σX2						uθ2					uθ2							uθ2
									1																m				1					2						m

В этом выражении можно выделить среднее арифметическое взвешенное показания и среднее арифметическое взвешенное поправки:

		ˆ		ˆ	ˆ
	Q = X				+ θ ,
которые, соответственно, равны:		ˆ		m
		X		= ∑g X j X j ;
				j=1
	θˆ			m
				= ∑gθj θj ,
				j=1

где нормированные веса каждого j-го значения показания и каждой j-й поправки

1

gX j

=

σ2X j

;

m

1

1

∑

+

2

2

σ

X j

u

j=1

θj

1

u2

gθj

=

θj

.

m

1

1

∑

+

2

2

=

σ

X j

u

θj

j 1

177

И.Ф. Шишкин. ТЕОРЕТИЧЕСКАЯ МЕТРОЛОГИЯ

________________________________________________________________

Среднее квадратическое отклонение средневзвешенного показания	ˆ	является
	X

мерой точности результата измерения, а аналог среднего квадратического отклонения

средневзвешенной поправки ˆθ - мерой правильности. Выражения для этих показателей качества результата многократного измерения с неравноточными значениями отсчета имеют вид:

m

σX = ∑g2X j σ2X j ; j=1

m

uθˆ = ∑gθ2 j uθ2 j .

j=1

Если точность показаний средств измерений неизвестна, но известны точно поправки, которые в эти показания нужно вносить, то формула среднего арифмети-

ческого взвешенного преобразуется следующим образом:

1

∑

1

∑

m

m

j=1 X j

+

j=1 θj

S

2

S

2

=

X

θ

,

Q

m

+

m

S X2

Sθ2

где

S X2 =

1

m

)2 ;

∑ ( X j −

X

m −

1 j=1

Sθ2 =

1

m

∑

(θj − θ)2 .

m −

1 j=1

Опять-таки можно выделить среднее арифметическое взвешенное показания и среднее арифметическое взвешенное поправки:

		ˆ		ˆ	ˆ
	Q =			X + θ ,
которые, соответственно, равны:
			m
		= ∑g X X j ;
	X
			mj=1
θ		= ∑gθθj ,

j=1

где нормированные веса каждого j-го значения показания и каждой j-й поправки

178

Часть I. ОБЩАЯ ТЕОРИЯ ИЗМЕРЕНИЙ

________________________________________________________________

1

g X

=

S X2

;

1

1

m

S X2

+

S θ2

1

g θ

=

S θ2

.

1

1

m

S X2

+

S θ2

Показателем точности результата измерения в данном случае служит

S

= mg2X S X2

=

S

ˆ

S 2

,

ˆ

X

θ

m

2

2

θ

S X

+ Sθ

показателем правильности -

S

= mg

θ2 Sθ2

=

S

θ

S 2

,

ˆ

X

m

2

2

θ

где

S X

+ Sθ

S 2

<1;

S

2

<1.

θ

X

SX2 + Sθ2

SX2

+ Sθ2

Благодаря рандомизации поправки, не только точность, но и правильность результата многократного измерения с неравноточными значениями отсчета по-

вышается, но не более чем в m раз.

Если в последнем случае в качестве результата измерения использовать не среднее арифметическое взвешенное, а среднее арифметическое

ˆ

1

m

1

m

ˆ

ˆ

∑ X j +

∑

Q m =

θ j = X m + θm ,

m

m

j=1

j=1

то показатели его точности и правильности

1

m

ˆ

2

S X

∑

S

=

X j − X m

=

;

m

m (m

− 1)

X

m

j=1

1

m

2

S θ

S

θˆ

=

∑j=1

(θ j − θm )

=

.

m (m − 1)

m

179