лекция 4

ЛЕКЦИЯ 4. Деформированное состояние материала в точке. Тензор деформаций. Обобщённый закон Гука

Для исследования деформаций мысленно вырежем вблизи произвольной точки тела элементарный параллелепипед (рис. 3.1). В результате различия перемещений точек параллелепипеда, его ребра удлиняются (укорачиваются), а первоначально прямые углы между ребрами искажаются. В соответствии с этим различают два вида деформаций – линейные и угловые . Деформации удлинения считаются положительными, а укорочения – отрицательными.

Угловые деформации или деформации сдвига , , представляют собой искажения прямых углов между ребрами элементарного параллелепипеда. При этом индексы указывают на то, в какой плоскости происходит угловая деформация. Деформации сдвига так же, как и касательные напряжения обладают свойством взаимности, то есть

, , . (4.1)

Объемная деформация равна сумме трех линейных деформаций

= . (4.2)

Деформированное состояние в точке характеризуется тремя деформациями в направлении осей x, y, z и тремя угловыми деформациями в плоскостях xy, yz и zx элементарного параллелепипеда, мысленно вырезанного в окрестности исследуемой точки (рис. 3.1). Деформации этого элемента в плоскости xy показаны на рис. 4.1 и соответственно равны ε_x, ε_y, γ_xy. При повороте координатных осей и граней параллелепипеда будут изменяться значения линейных деформаций ε и углов сдвига γ.

С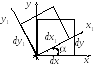овокупность линейных и угловых деформаций для всевозможных направлений осей, поведённых через исследуемую точку, определяет деформированное состояние в точке.

Рис. 4.1.

Подобно изменению напряжений на наклонной площадке меняются и деформации в новой системе координат, повёрнутой на угол α относительно начальной. Можно провести аналогию между выражениями для напряжений и деформаций, заменив в выражениях для напряжений нормальные напряжения линейными деформациями, а касательные – половинами углов сдвига получится выражение для деформаций (4.3).

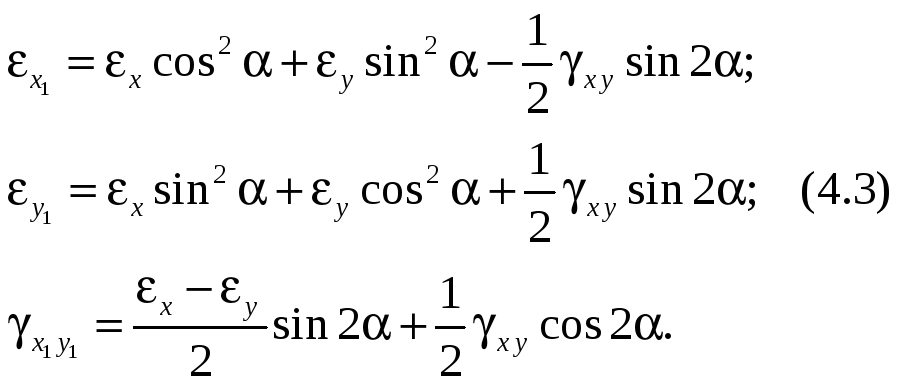
По этой аналогии можно указать такие три ортогональных направления 1, 2, 3, для которых отсутствуют углы сдвига, а линейные деформации ε₁, ε₃ приобретают максимальное и минимальное значения. Эти направления и деформации называются главными. Выражение по аналогии с формулами для плоского напряжённого состояния записаны ниже.

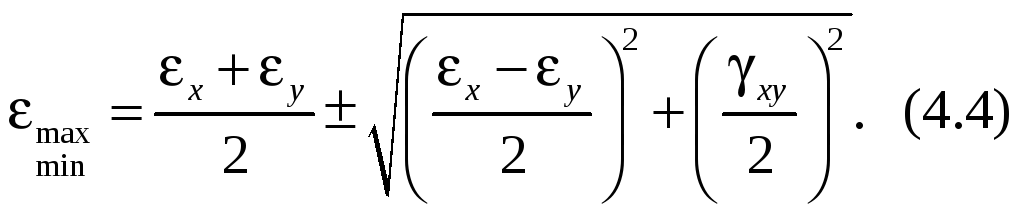
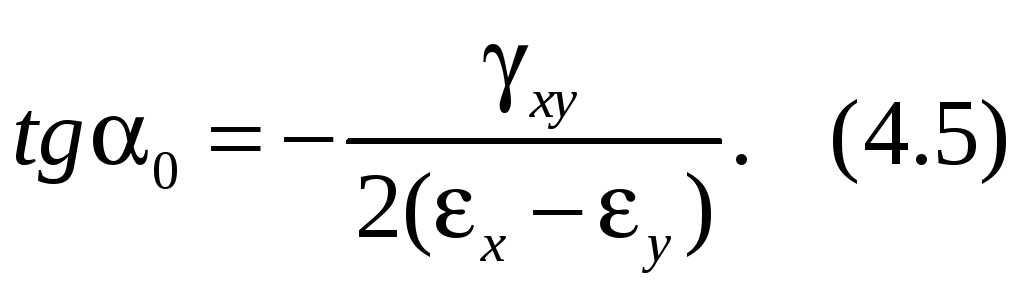
В точках изотропного упругого тела направления главных напряжений и главных деформаций всегда совпадают, в случае анизотропии и неупругости этого может и не быть.

Различают малые и большие деформации.

При малых деформациях деформированное состояние элементарного параллелепипеда определяется тензором деформаций, который, как и тензор напряжения является симметричным тензором второго ранга

Тензор деформаций так же, как и тензор напряжений можно представить в виде суммы шарового тензора и девиатора деформаций

= + . (4.7)

В матричной форме шаровой тензор и девиатор деформаций имеют следующий вид

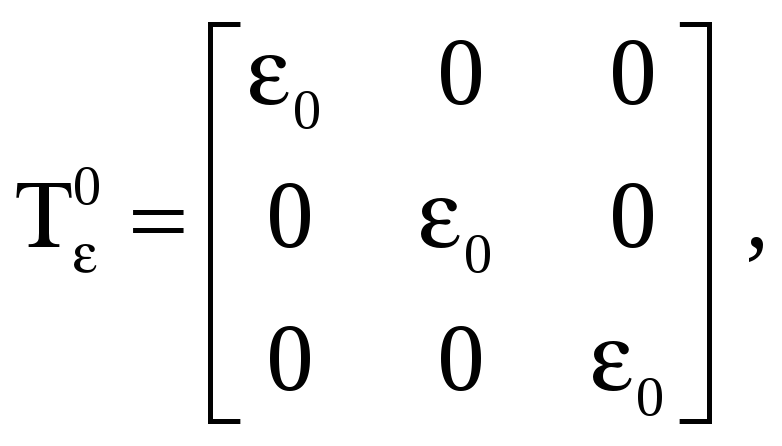
Величина называется средней деформацией и равна

. (4.9)

При суммировании компонент шарового тензора деформаций с учетом получим .

Шаровой тензор деформаций определяет объемную деформацию параллелепипеда без изменения его формы.

При сложении компонент девиатора деформаций, стоящих на его главной диагонали получим .

Таким образом, девиатор деформаций характеризует изменение формы элементарного параллелепипеда без изменения его объема.

Обобщённый закон Гука имеет вид (4.10).

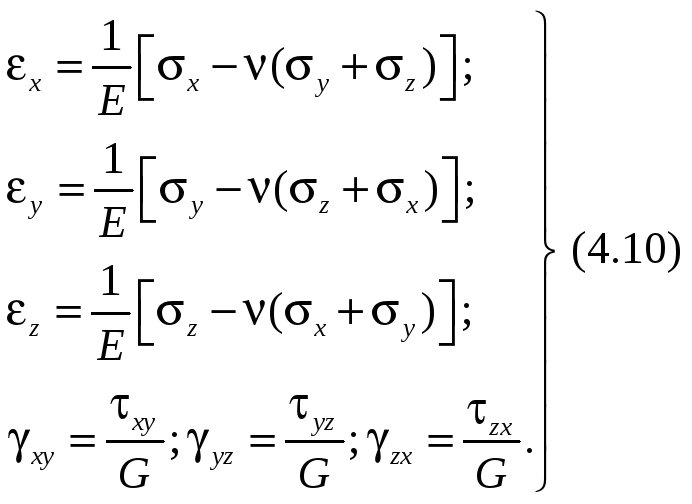
Для главных деформаций этот закон запишется через главные напряжения в виде (4.11).

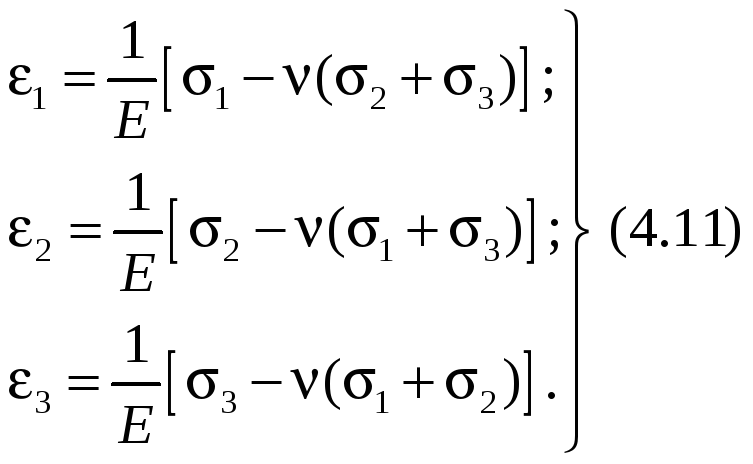
Здесь ν = ε_y/ε_x - коэффициент Пуассона, E – модуль Юнга, G = E/2(1+ν) – модуль сдвига.

3