Лекции по физике

Итак, доказана Теорема об изменении кинетической энергии системы:

Изменение кинетической энергии системы материальных точек равно работе всех сил, действующих на точки системы.

Aвсехсил = W		− W	(6.4)
12	K2	K1

Примечание: Следует отметить, что работу внутренних сил системы также следует учитывать, т.к. они изменяют кинетическую энергию системы.

6.2. Закон изменения и закон сохранения полной механической энергии

Рассмотрим систему из n материальных точек, на которые действуют и консервативные и неконсервативные силы. Согласно (6.4) работа всех сил

A12всехсил затрачивается на приращение кинетической энергии системы. Разобьём

эту работу на работу консервативных сил А12конс и работу неконсервативных сил

А12неконс.

		А12конс + А12неконс = WK2 – WK1
Но, в соответствии с (4.10), А				конс	= W	– W		- работа
				12	П1	П2
консервативных сил равна убыли потенциальной энергии.Отсюда:
(W	K2	+ W	) – (W		+ W	)= А	неконс
		П2		К1	П1		12
Сумму кинетической и потенциальной энергии системы называют полной
механической энергией системы и обозначают Е:
		Е = WK + WП						(6.5)

Итак, мы получили закон изменения полной механической энергии:

Приращение полной механической энергии системы материальных точек равно работе неконсервативных сил, действующих на точки системы:

Е – Е = А		неконс	(6.6)
2	1	12

Если неконсервативных сил нет, то механическая энергия системы остаётся постоянной, и мы получаем закон сохранения полной механической энергии:

В консервативных системах полная механическая энергия системы сохраняется.

Е ≡ WК + WП =const

(6.7)

6.3 Упругое и неупругое столкновения

Абсолютно неупругий удар – это удар, при котором после столкновения тела “слипаются” и далее движутся вместе.

При этом часть кинетической энергии переходит в тепло, поэтому полная механическая энергия при неупругом ударе не сохраняется. С другой стороны, выполняется закон сохранения

импульса: Pсистдоудара = Pсистпослеудара .

23

Для двух тел получим:
m V + m		2	V = (m		+ m	)V'	, где V и V скорости тел до удара, а V'						-
1	1		2	1	2			1		2
скорость слипшихся тел после удара. Из этого уравнения легко получить V' .
				V'	= (m V + m V )/(m + m						)	(6.8)
					1	1	2	2	1	2

Отметим, что если два тела сталкиваются неупруго, то в системе центра масс они двигаются вдоль одной прямой навстречу друг другу, а после удара – покоятся, рис. 6.1.

Абсолютно упругим называют удар, при котором потери механической энергии нет. (Выполняются закон сохранения энергии и закон сохранения импульса).

Следует отметить, что в природе ничего “абсолютного” не бывает, но некоторые удары с высокой точностью можно считать абсолютно упругими.

Рассмотрим абсолютно упругий удар в системе центра масс. Напомним, что

в ней VC = 0.

При механической деформации шары аналогичны сжатым пружинам, которые затем выпрямляются. После удара (в системе центра масс) шары как бы поменяют знак своей скорости.

Для произвольных начальных							скоростей V1 и			V2 скорости тел после
			′			′	описываются формулами:
абсолютно упругого удара V				и V
		1				2
		2m2	V2 +			(m1 − m2 )V1
V1′ =
					m1 + m2
										(6.9)
′	=	2m1 V1			+	(m2 − m1 )V2
V2
					m1 + m2

где m1 и m2 – массы соответствующих тел.

6.4. Общефизический закон сохранения энергии

Классическая механика учитывает лишь кинетическую энергию макроскопического движения тел и их потенциальную энергию, отвлекаясь от атомистического строения вещества.

На самом деле при трении, неупругом ударе и т.д. энергия не пропадает, а переходит в кинетическую и потенциальную энергию теплового движения атомов и молекул, (во внутреннюю энергию). Поэтому полное, с учётом энергии атомов, количество энергии в изолированной системе тел всегда остаётся постоянным.

24

Это общефизический закон сохранения энергии. Его нельзя вывести из уравнений механики, т.к. он имеет общую универсальность.

В основе закона сохранения энергии лежит однородность времени, т.е. тот факт, что замена момента времени t1 моментом времени t2 при сохранении координат и скорости тел не изменяет законов движения системы.

Лекция 7 Закон сохранения момента импульса

Ликбез. Напомним свойства векторного произведения.

Вектор c = a× b называют векторным произведением векторов a и b, если он обладает следующими 3-мя свойствами:

1) Модуль вектора c вычисляется по формуле:

		=				×				sinα , где α - угол между векторами
c				a				b

a и b. Направление вектора c определяется правилами 2 и 3.

2) Вектор c перпендикулярен и к первому вектору (a) и ко второму (b): c a ; c b следовательно, вектор c перпендикулярен плоскости, в которой лежат вектора a

и b. Но перпендикулярно плоскости будут два направления: и вверх, и вниз. Выбрать верное позволяет правило «буравчика»:

3) Ручку буравчика нужно поворачивать по кратчайшему пути от первого

вектора (a) ко второму (b), тогда перемещение самого буравчика укажет направление вектора c .

=

×

sin0o = 0.

Пример 1. Если вектор a

b , то

c

a

b

=

×

sin90o = a b.

Пример 2. Если вектор a b, то

c

a

b

В этом случае модуль вектора c принимает максимально возможное значение.

Пример 3. Если векторы a и b поменять местами см. рис. 7.1., то

изменяется знак векторного произведения: b× a = −a× b.

Примечание. Иногда векторное произведение обозначают квадратными

скобками.

a×b ≡ [a×b]

Конец ликбеза.

7.1 Момент силы и момент импульса относительно неподвижной точки

Введём следующее определение:

Моментом силы относительно неподвижной точки О называют векторное произведение радиуc-вектора r , идущего от точки О к точке приложения силы, на силу F .

25

L = r × p

Моментом импульса

M = r× F

(7.1)

Момент силы M это такая физическая величина, которая приводит к угловому ускорению вращающихся тел. Модулю момента силы можно дать

наглядное толкование:

M = F r sinα = F"плечо", где введено понятие «плечо».

По определению «плечо» = r sinα, соответствует кратчайшему расстоянию от точки О до линии, вдоль

которой действует силаF .(см. рис. 7.2). Если на материальную точку действуют N различных сил, то результирующий момент сил определяется как векторная сумма

моментов всех сил.

	N		N
Mрез	= ∑Mi		= ∑ri	× Fi (7.2)
	i=1		i=1

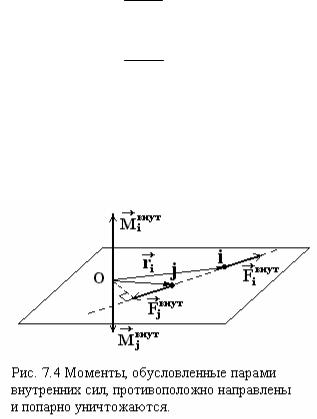
L материальной точки массой m относительно неподвижной

точки	О	называется векторное произведение
радиус-вектора r			на	импульс материальной
точки	p = m V .
		L = r× p = r× m V			(7.3)
Для		системы	из	N материальных	точек

суммарный момент импульса L равен векторной сумме моментов импульса всех точек.

N		N
L = ∑Li		= ∑ri×pi	(7.4)
i=1		i=1

7.2 Закон изменения момента импульса. (Уравнение моментов)

Пусть материальная точка массой m движется относительно неподвижной точки О со скоростью V . Продифференцируем её момент импульса

по времени:

Но dr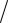dt = V ,

параллельные векторы мы получаем:

dL = dr × p+ r× dp dt dt dt

поэтому в первом произведении векторно умножаются

V и mV , что даёт ноль. В свою очередь dpdt = F, и

26

Miвнут

Mвнутj

	dL				dL
		= r	× F	или		= M	(7.5)
	dt				dt

Это закон изменения момента импульса (уравнение моментов) для одной материальной точки.

Для системы из N материальных точек уравнение (7.5) можно написать для каждой точки системы, а затем сложить: (при этом результирующие силы Fi представим в виде суммы внешних и внутренних сил: Fi = Fiвнут + Fiвнеш ).

dL1 = r1 (F1внут + F1внеш ) = r1 F1внут + r1 F1внеш

dt

dL2 = r2 (F2внут + F2внеш ) = r2 F2внут + r2 F2внеш

dt

dL	N
		= r	(Fвнут + Fвнеш ) = r			Fвнут	+ r		Fвнеш
dt		N	N	N	N	N	N		N
					Моменты			сил,		обусловленные
					внутренними силами Fiвнут , попарно
					уничтожатся.			Действительно,			по
					третьему закону					Ньютона	при
					взаимодействии точек системы между
					собой , например, точки i и j на
					рисунке 7.4, возникающие внутренние
					силы	равны	по	величине, действуют

вдоль одной прямой, следовательно, имеют одинаковое “плечо” и одинаковые по

модулю моменты сил. Но эти моменты и будут противоположно

направлены (рис. 7.4), т.к. Fiвнут и			Fjвнут имеют противоположные направления.
В результате для системы материальных точек получаем закон изменения
момента импульса:
		dLсист
			= Mвнеш	(7.7)
		dt	рез
	N
где Lсист	= ∑Li - момент импульса системы материальных точек,

i=1

27

	N
Mрезвнеш = ∑ri ×Fiвнеш			- результирующий момент	внешних сил,
	i=1
действующих на точки системы.
Полученное		уравнение	справедливо и для моментов,	вычисляемых не

относительно точки О, а относительно некоторой оси ОО’. При этом “плечо” силы или импульса – это расстояние от линии действия F или P до оси ОО’. Моменты Mz или Lz относительно оси равны проекции на эту ось моментов

M или L, рассчитанных относительно любой точки этой оси.

Если точка О, относительно которой производится расчет моментов, находится в начале координат x,y,z, то справедливы уравнения:

dL

x

= M

;

dLy

= M

;

dL

z

= M

(7.8)

x

y

z

dt

dt

dt

где Lx ,Ly ,Lz ,Mx ,My ,Mz рассчитываются относительно соответствующих

осей, или рассчитываются относительно точки О, а затем проектируются на оси x,y,z.

7.3 Закон сохранения момента импульса

Из закона изменения момента импульса для системы материальных точек:

dLсист = Mвнешрез

dt

следует, что в замкнутых системах, где внешних сил нет и Mвнешрез = 0, суммарный момент импульса Lрез = const , т.е. сохраняется, и мы получаем:

Закон сохранения момента импульса: В замкнутой системе материальных точек момент импульса сохраняется.

	N
	= ∑ri ×pi	= const
Lсист			(7.9)
	i=1
Примечание: Момент импульса сохраняется и			в незамкнутой системе

материальных точек, если результирующий момент внешних сил Mвнешрез равен

нулю.

Закон сохранения момента импульса справедлив не только в механике, но и во всём материальном мире. В основе закона сохранения момента импульса лежит изотропность пространства, т.е. неизменность законов движения при повороте системы в пространстве на любой угол.

7.4 Движение в поле центральных сил

Силы, действующие на материальную точку, называются центральными, если они определяются только расстоянием от материальной точки до некоторой неподвижной точки, называемой центром сил, и направлены всюду либо от центра сил либо к центру сил.

28

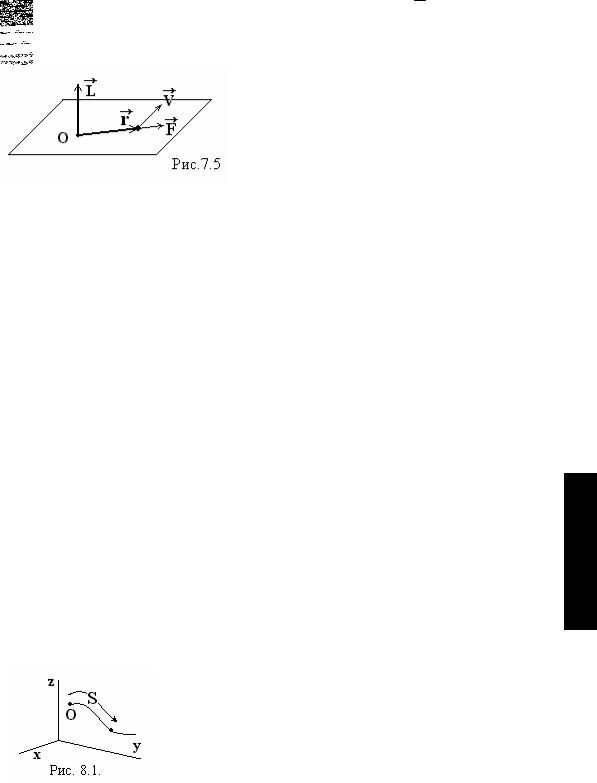
Если центр сил принять за начало координат О, то центральные силы можно описать зависимостью:

F = f(r) r		(7.10)

r

Пример: движение спутников в поле тяжести Земли.

В поле центральных сил вектор силы F направлен вдоль или навстречу радиус-вектору r .

Очевидно, что моменты сил, создаваемые центральными силами, равны нулю. Поэтому

момент импульса L в поле центральных сил сохраняется:

L = const

(7.11)

Постоянство момента импульса означает, что движение происходит в одной плоскости.

Можно показать, что поле центральных сил консервативно. Поэтому полная механическая энергия материальной точки в этом поле сохраняется.

E=Wк+Wп=const.

(в поле центральных сил)

(7.12)

Лекция 8 Твёрдое тело в механике 8.1. Степени свободы. Обобщённые координаты

Числом степеней свободы называется минимальное количество независимых переменных, которые полностью задают положение всех точек системы в пространстве.

Примеры:

1 точка – 3 степени свободы (x,y,z) или (r,ϕ,ψ),

2точки – 6 степеней свободы (x1,y1,z1, x2,y2,z2),

2связанные точки – 5 степеней свободы

(каждая связь уменьшает число степеней свободы на 1), 3 точки – 9 степеней свободы, 3 связанные точки – 6 степеней свободы (9-3связи=6)

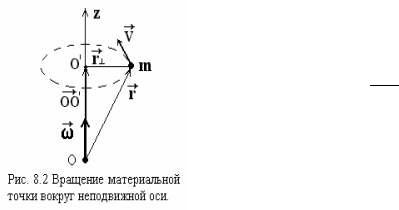
движение точки вдоль кривой – 1 степень свободы (S – расстояние от начала О) (Рис.8.1).

Твёрдое тело имеет 6 степеней свободы т.к. в качестве независимых параметров можно взять координаты 3-х любых точек тела, не лежащих на одной прямой.

Обобщёнными координатами называются любые переменные q1,q2…qn, число которых n равно числу степеней свободы системы и которые полностью задают положение всех точек системы.

Примеры: Для одной точки декартовы координаты x,y,z являются обобщёнными. Другой вариант – координаты точки в сферических координатах r,ϕ,ψ. Твёрдое тело, одна из точек которого закреплена, имеет 3 степени свободы (6-3=3). Твёрдое тело, у которого ось вращения фиксирована, имеет 1

29

степень свободы (3-2=1). При этом обобщённой координатой может служить угол поворота тела вокруг оси.

8.2 Уравнение движения и равновесия твёрдого тела

Т.к. твёрдое тело можно представить как систему материальных точек, то для него справедливо уравнение движения:

			dP		= F	внеш	(8.1)
			dt
и закон изменения момента импульса:
		dL		= Mвнеш			(8.2)
Здесь: P = ∑Pi			dt
	- суммарный импульс системы материальных точек,
Fвнеш = ∑Fвнеш	- результирующая внешних сил, действующих на систему,
i

L = ∑Li - суммарный момент импульса системы,

Mвнеш = ∑Miвнеш - результирующий момент внешних сил, действующих на систему.

Итак, для описания движения твёрдого тела, которое имеет 6 степеней свободы, т.е. 6 обобщённых координат, есть 2 векторных уравнения (или 6 скалярных). Эти 6 уравнений полностью определяют движение тела в пространстве, т.е. изменение 6-ти переменных (обобщённых координат).

Если твёрдое тело покоится, то получаем условия равновесия твёрдого тела:

Fвнеш = 0,

Mвнеш = 0

(8.3)

Это необходимые условия равновесия твёрдого тела. Но эти условия не являются достаточными, т.к. при их выполнении центр масс может двигаться

равномерно и прямолинейно, P = const , а само тело может дополнительно равномерно вращаться, имея L = const .

8.3 Вращение твёрдого тела

Пусть материальная точка массой m вращается вокруг неподвижной оси ОО´, вдоль которой направлена ось z, рис.8.2. Для нее справедливо уравнение вращательного движения:

dL = Mвнеш

dt

При этом L и Mвнеш рассчитаны относительно произвольной точки О, лежащей на оси. Проекции L и Mвнеш на ось z называют моментом импульса Lz относительно оси z и моментом силы Mz

относительно оси z.

30

Найдём, чему равно Lz для произвольной материальной точки массой m.

Сначала найдём L относительно точки О, рис. 8.2.

L = r× mV = (00′ + r )× mV = 00′ × mV+ r × mV

Здесь мы учли, что r = 00′ + r . Чтобы получить Lz, необходимо спроектировать L на ось z. Проекция вектора [00′ × mV] на ось z равна нулю, т.к. это векторное произведение перпендикулярно 00′. Второе векторное

произведение	r	× mV параллельно оси z, т.к. перпендикулярно плоскости, в
которой лежат вектора r				и V . Следовательно, с учётом того, что V = r ω,
получаем:				= r mV = r m(r ω) = mr2
		L	z					ω
По определению, величина					J = m r2	называется		моментом инерции

материальной точки относительно оси.

Здесь r - расстояние от точечной массы m до оси.

Итак, момент импульса Lz материальной точки относительно оси вращения Z равен:

Lz = Jz ω

(8.4)

где Jz – момент инерции относительно оси z, ω – угловая скорость.

Если у нас вращается не одна материальная точка, а твёрдое тело, то для него момент импульса относительно оси складывается из моментов импульса каждой точки тела:

Lz = ∑mi r2i ω = ω∑mi r2i = Jz ω

(8.4)

где Jz = ∑mi r2i - является моментом инерции всего тела относительно

оси z. Строго говоря, для сплошного твёрдого тела момент инерции является не суммой, а интегралом, но этот вопрос будет подробнее рассмотрен в следующем разделе.

Уравнение динамики тела, вращающегося относительно оси z, получается проектированием уравнения (8.2) на ось:

		dLz		= Mвнеш
		dt			z
	или	Jz	dω		= Mвнешz
			dt
Где Mвнеш	- проекция на ось Z результирующего момента внешних сил.
z

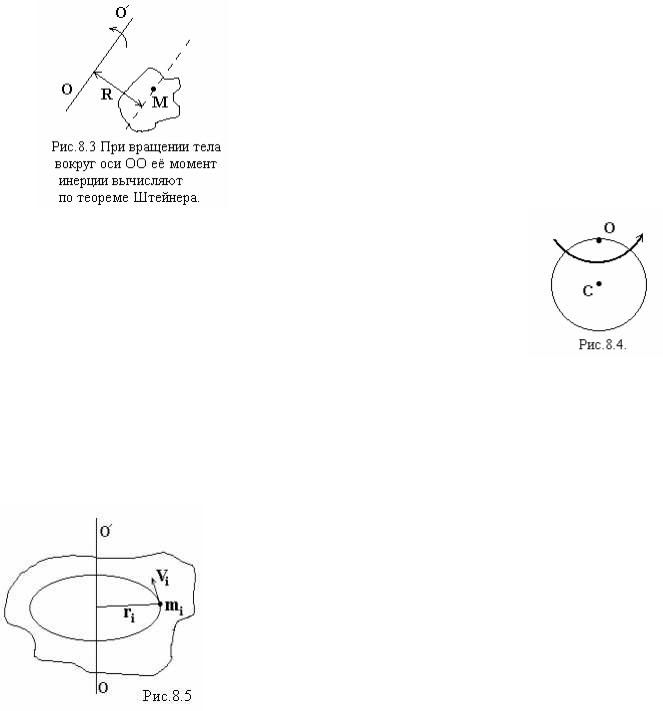
8.4 Момент инерции твёрдого тела. Теорема Штейнера

(8.5)

(8.6)

Для расчёта момента инерции твёрдого тела относительно оси, необходимо разбить тело на элементарные массы dm, для каждой рассчитать элементарный

31

J = ∫r2dm

dJ = r2dm

момент инерции и проинтегрировать все элементарные моменты инерции по всему объёму тела V:

(8.7)

Но dm = ρdV, где ρ - плотность тела,Vа dV - элементарный объём. Поэтому (8.7) можно выразить по-другому:

	2	(8.8)
	J = ∫r ρdV

V

При расчётах момента инерции тел, очень полезна теорема Штейнера, которая имеет следующий вид:

JОО´=JC + mR2

(8.9)

где JОО´ - момент инерции относительно оси ОО´; JC – момент инерции относительно оси параллельной ОО´ и проходящей через центр масс тела C; m – масса всего тела; R – расстояние между осями.

Пример: Рассчитаем момент инерции обруча, вращающегося на гвозде вокруг точки О. По теореме Штейнера, учитывая, что момент инерции обруча относительно центра масс С равен mR2, получим:

Jo=JC + mR2 = mR2 + mR2 = 2mR2

8.5 Кинетическая энергия при вращении тела вокруг оси

Полная кинетическая энергия любого тела складывается из кинетической энергии всех материальных точек тела:

∑

∑

2

∑

2

2

∑

2

W

=

W

=

miVi2

=

mi

ω2ri2

= ω2

m r2

=

Jzω2

K

Ki

i i

Итак, кинетическая энергия вращающегося тела

равна:

W =

J

ω2

z

(8.10)

K

2

где J – момент инерции тела относительно оси вращения Z;

ω- угловая скорость вращения тела.

8.6Кинетическая энергия тела при плоском движении

Плоским называют движение, при котором все материальные точки движутся, оставаясь в параллельных плоскостях.

Пример: Колесо при движении велосипеда.

32