Лекции по физике

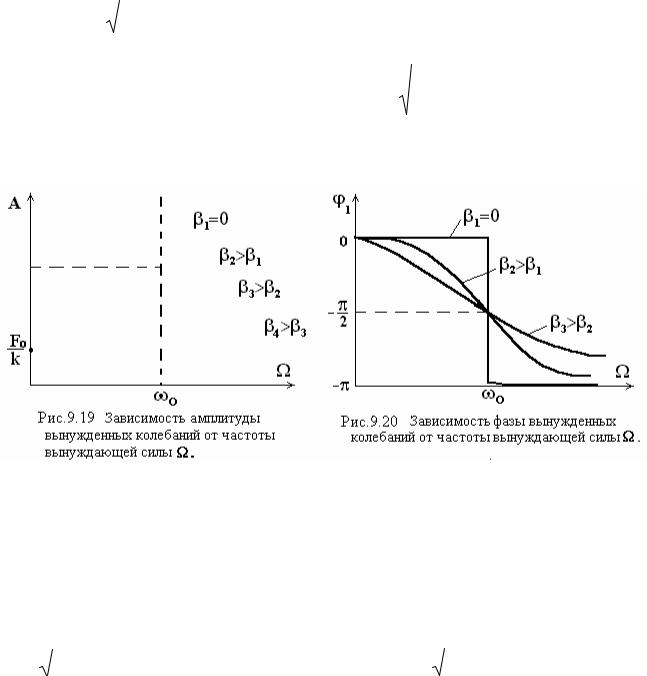
9.10 Вынужденные колебания. Резонанс

Если на колебательную систему действует периодическая внешняя вынуждающая сила F(t), то колебания называют вынужденными.

Наиболее часто встречается гармоническое возмущение F(t)=FocosΩt ,где Ω − частота возмущающей силы. Дифференциальное уравнение вынужденных колебаний имеет вид:

mɺxɺ+ rxɺ + kx = Fo cos Ωt

(9.23)

Его решением является гармоническое колебание, происходящее с частотой вынуждающей силы:

x =Acos(Ωt+ϕ1)

(9.24)

где A =

Fo

,

tgϕ1 =

2βΩ

m

ω2o − Ω2

(ω2o − Ω2 )2 + 4β2Ω2

(9.25)

β =

r

,

ω =

k

2m

o

m

На рисунках 9.19 и 9.20 приведены зависимости амплитуды А и фазы ϕ1 от частоты Ω внешней силы (резонансные кривые).

1.

При Ω << ωο амплитуда A ≈

Fo

=

Fo

имеем статическую деформацию под

mω2

k

действием постоянной силы Fo.

2.

При Ω >> ωο амплитуда A ≈

Fo

, т.е. амплитуда быстро уменьшается с

mΩ2

ростом частоты Ω.

3.

Максимальная

амплитуда

Amax

соответствует

частоте резонанса:

Fo

Ω

= ω2o − 2β2

при этом A

=

, где ω =

ω2o − β2 - собственная

рез

max

2βmω

43

циклическая частота колебаний системы. При малом коэффициенте затухания β резонанс наступает при частоте возмущений близкой к частоте собственных колебаний системы.

Отметим, что выражения (9.25) для амплитуды и фазы вынужденных колебаний относятся к установившимся колебаниям, которые получаются в результате длительного воздействия вынуждающей силы. В такое состояние колебательная система переходит не сразу, а в результате некоторого переходного процесса, изучение которого выходит за рамки нашего курса.

9.11 Параметрические колебания

Параметрическими называются колебания системы, возникающие при условии, что один или несколько параметров колебательной системы периодически изменяются.

Пример: Когда мы приседаем и встаём на качелях. При этом периодически меняется положение центра тяжести физического маятника, и колебания не затухают.

9.12Модулированные колебания

1.Амплитудная модуляция (рис. 9.21). В общем случае модулированные по амплитуде колебания имеют вид:

x=A(t)cos(ωt+ϕ) ω=const , ϕ=const Если A(t)=Ao( 1+δcos Ωt ), то

x=Ao(1+δcosΩt)cos(ωt+ϕ)=Aocos(ωt+ϕ)+ +(Aoδ/2)cos[(ω+Ω)t+ϕ]+(Aoδ/2)cos[(ω−Ω)t+ϕ]

При такой модуляции, сигнал состоит из трёх гармонических слагаемых. Это можно изобразить в виде спектра (рис. 9.22). Спектр - это изображение процесса в виде набора гармонических слагаемых.

2. Частотная модуляция (рис. 9.23), в общем случае описывается соотношением:

x=Aocos[ω(t)t+ϕ], где Ao=const , ϕ=const

44

3. Фазовая модуляция:

x=Aocos[ωοt+ϕ(t)],

где Ao=const , ωο= const

Лекция12. Элементы специальной теории относительности, (СТО) 12.1 Преобразования Галилея. Принцип относительности Галилея

Принцип относительности Галилея гласит, что во всех инерциальных системах законы классической механики одинаковы. Докажем его.

Пусть инерциальная система k неподвижна, а k´ движется с постоянной скоростью V относительно системы k . Тогда в классической механике:

			r = V t + r′	, t = t′
			o
Или в проекциях:		и обратно
x = x′ + V t		x′ = x − V t
	o		o
y = y′		y′ = y
z = z′		z′ = z
t = t′		t′ = t

Эти преобразования называют преобразованиями Галилея. Исходя из (12.1) найдём связь скоростей и ускорений:

dr

dr

′

dr

′

V =

= V

+

= V

+

= V

+ V′

dt′

dt

o

dt

o

o

Мы получим закон сложения скоростей в классической механике.

V′ = V− Vo

	Найдём связь ускорений:
	a =	d V	=	d V′		= a′	, a = a′
		dt		dt′

(12.1)

(12.2)

(12.3)

(12.4)

Мы доказали, что ускорения не изменяются в различных инерциальных системах отсчёта, т.е. инвариантны к преобразованиям Галилея. Кроме того, силы в классической механике зависят лишь от взаимного расположения тел

r	= r	− r	и относительных скоростей V		= V − V а эти величины также
12	1	2		12	1	2
инвариантны к преобразованиям Галилея. Следовательно:
			F′	= F		(12.5)
			ik	ik

45

Из (12.4) и (12.5), с учётом одинаковости масс в различных инерциальных системах, получаем, что второй и третий законы Ньютона инвариантны к преобразованиям Галилея.

в системе	k´		ma′ = F′	F′	= −F′
		ma = F		ik	ik
в системе	k		F = −F
			ik	ik

Принцип относительности Галилея доказан.

12.2 Постулаты СТО (постулаты Эйнштейна)

Опыт показывает, что нельзя выделить ”главную” инерциальную систему – все системы эквивалентны.

1-ый Постулат СТО. Принцип относительности: Все законы природы одинаковы во всех инерциальных системах отсчёта.

Никакими опытами не отличить, движется ли инерциальная система или нет. Опыт показывает, что взаимодействие между телами распространяется не мгновенно, а ограничено скоростью света в вакууме, которую обозначают буквой С. Майкельсон и Морли (с 1880 по 1887 г.г.) показали, что скорость света вдоль орбиты Земли и поперёк неё одинакова. Постоянство скорости света следовало и из уравнений Максвелла. Отсюда Эйнштейн сделал смелый вывод о том, что скорость света во всех инерциальных системах одинакова, что это фундаментальное свойство природы, которое нужно констатировать как опытный факт.

2-ой Постулат СТО: Скорость света во всех инерциальных системах отсчёта постоянна.

Эти два постулата сформулировал Эйнштейн в 1905 году.

Эти два простеньких с виду постулата приводят к удивительным выводам, которые произвели революцию в физике.

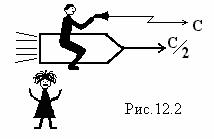
Рассмотрим простой пример. Пусть Вася летит на ракете со скоростью С/2 относительно Маши, и в её честь выпускает вперёд луч света. За 1 секунду свет должен убежать от Васи на расстояние С, но за эту секунду и сам Вася улетит от Маши на С/2. Значит свет за 1 секунду удалится от Маши на расстояние С+С/2. А это

противоречит требованию о том, что свет в Машиной системе отсчёта имеет скорость С.

Это противоречие приводит к выводу о том, что, либо размер движущихся тел сокращается, либо время в разных системах течёт по-разному. Рассмотрим этот вопрос более подробно.

12.3 Преобразования Лоренца

Рассмотрим пример: Поезд (система отсчёта k´) движется со скоростью V мимо стрелочника (система отсчёта k). В момент, когда последний вагон поравнялся со стрелочником, из него был послан световой сигнал машинисту.

46

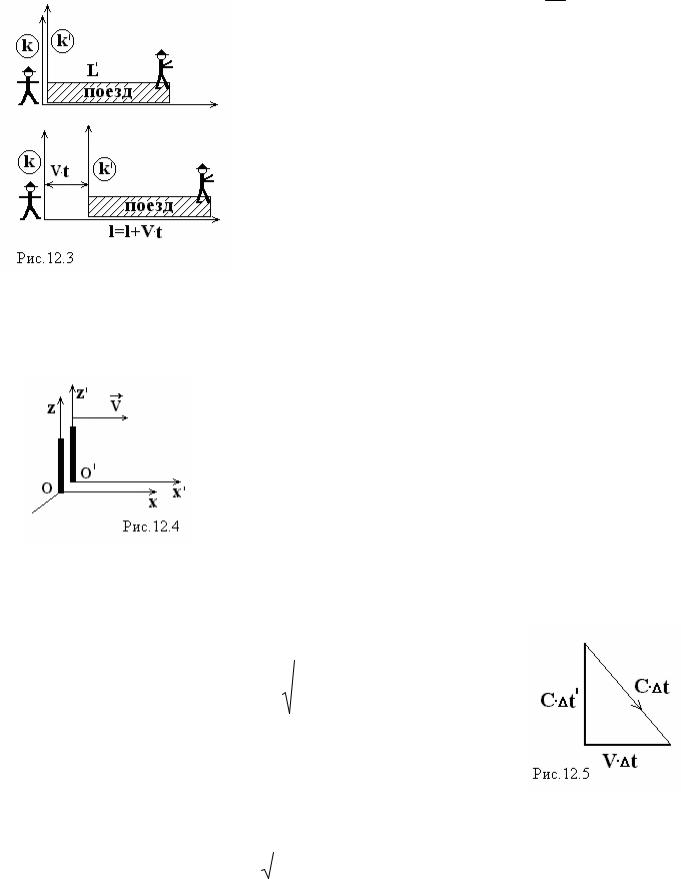
В системе k´ (машинист) C = L′ t′

L′ - длина поезда в k´,

t′ - время прохождения света к машинисту.

	В	системе			k	(стрелочник)
C =	L + Vt	=	L	+ V
	t		t				L′
	Очевидно, что				равенство:				=	L	+ V
							t′
										t

несовместимо

с условием L´ = L, t´ = t. Значит, либо L´ < L, т.е. поезд с точки зрения стрелочника короче, либо

t´ > t, время в движущейся системе идёт медленнее.

Оказывается, имеет место и то и другое: и сокращение длины и замедление времени.

Снабдим систему k и k´ универсальными часами: за единицу времени

	примем время, за которое свет проходит некоторый
	вертикально расположенный									эталонной длины
	стержень. В момент совпадения т. О и т. О´, стержни
	можно сравнить и взять одинаковой длины.
	Рассмотрим интервал времени между событиями,
	когда свет проходит стержень в системе k´ сверху
	вниз. С точки зрения наблюдателя k´ это происходит
	за t´ и длина стержня С t´! С точки зрения
наблюдателя k свет распространяется наклонно в течение										t и будет снесён на
расстояние V	t.
Из теоремы Пифагора (C		t´ )2 + (V					t)2 = (C t)2
Откуда:
	t′ =	t 1−			V2
					C2
Итак,	t´ длительность	события измеренного в k´
неподвижными в k´ часами (собственная длительность
события) всегда меньше, чем		t его длительность, измеренная
в системе k. Имеем замедление времени в движущейся (k´) системе.
	t =		t′				, где β2 =	V2		(12.6)
		1− β2						C2

Аналогично можно показать, что размеры движущихся тел в направлении движения сокращаются

47

	L = L′ 1−	V2	(12.7),
		C2

где L’- собственная длина тела, измеренная неподвижной относительно тела линейкой.

Исходя из двух постулатов, Эйнштейн вывел в 1905 году правила перехода из

одной инерциальной системы в другую:

x′ =

2

x = x′ + Vt′

x

− Vt

1− β

1− β2

y' = y

y = y′

и обратно:

(12.8)

z = z′

z' = z

t′ +

V

x′

t −

V

x

C2

C2

t =

t′ =

1

− β

2

1

− β

2

где β2 = V2 .

C2

Эти преобразования носят имя Лоренца, он вывел их в 1904 году из уравнений Максвелла, но не смог их правильно интерпретировать.

Для медленных движений (V<<C) β2 = V2 → 0, преобразования Лоренца

C2

переходят в преобразования Галилея (релятивистская механика переходит в классическую механику).

12.4 Преобразование и сложение скоростей

Пусть в системе k´ тело движется со скоростью V ′, имея следующие составляющие:

VX′ = dx′′ ,VY′ = dy′′ ,VZ′ = dz′′ dt dt dt

Найдём скорость тела V в системе k.

	По определению: V =					dx
					X	dt
			′ + Vt′						dx′ + Vdt		′
	но x =	x			, поэтому			dx =
			1− β2						1− β2

t′ +

V

x′

dt′ +

V

dx′

t =

C2

, соответственно dt =

C2

1− β2

1

− β2

48

Подставляя dx и dt в определение скорости VX , получим:

dx′ + Vdt′

dx′

+ V

V =

= dt′

=

X

V′ + V

X

V

V

dx′

V V′

dt′ +

dx′

1+

1+

X

C2

C2

dt′

C2

В результате мы получили релятивистский закон сложения скоростей:

	=	V′	+ V
VX		X		(12.9)
		V V′

	1+	X
		C2

Поскольку в поперечных направлениях размеры не меняются, то dy´= dy и для VY и VZ получаем:

′

′

V = dy = dy

1

−β

2

1−β

2

= VY

Y

dt

′

+

V

′

1+

V V′

X

dt

dx

C2

C2

Аналогично V =	V′			1− β2
		Z
			V V′
Z	1	+
				X
				C2

Возвратимся к примеру с Васей и Машей. Если частица (свет, выпущенный Васей) движется в системе k´ со скоростью света VX´ =C, то в k ( с точки зрения Маши) ее скорость:

	V =	C + V	=	(C + V)	C = C
		V C		(C + V)
	X

1+

C2

т.е. постулат Эйнштейна не нарушается.

12.5 Интервал

Из преобразований Лоренца видно, что при переходе из одной инерциальной системы в другую меняются не только координаты событий, но и соответствующие им моменты времени.

Расстояние при преобразованиях Лоренца сокращается вдоль движения и сохраняется поперёк, следовательно l12 ≠l12´

l	=	(x		1	− x	2	)2	+ (y	1	− y	2	)2	+ (z	1	− z	2	)2
12
	′ =
l			(x′		− x′ )2			+ (y′		− y′ )2			+ (z′		− z′ )2
12				1		2			1		2			1		2

Неизменным (инвариантным) при преобразованиях Лоренца остаётся так называемый интервал между событиями.

S =	C2 (t	1	− t	2	)2 − l 2	(12.10)
12					12

49

где t1 и t2 – время первого и второго события, а l12 – расстояние между точками, в которых эти события произошли.

12.6.Понятие о релятивистской динамике

Вклассической механике масса тел m не зависит от скорости тела. Однако в конце 19 века в опытах по разгону электронов в электрических полях выяснилось, что с ростом электрического поля электроны разгонялись медленнее, чем это следовало из формул классической механики. На основе этих

идругих экспериментов был сделан вывод о том, что масса частиц растет с увеличением скорости частиц.

Теория о зависимости массы m движущегося тела от его скорости держалась более 100 лет вплоть до наших дней.

Однако более глубокие исследования показали, что масса тела m не зависит от его скорости и остается постоянной (инвариантной) при переходе от одной инерционной системы отсчета к другой.

Всовременной специальной теории относительности (СТО) справедливы следующие положения:

1.Масса тела m определяется энергией покоя тела Ео и не зависит от скорости тела.

mc2 = Eo

(12.11)

2.Движущееся тело, кроме энергии покоя Eo обладает и кинетической энергией Wk, а полная энергия тела равна:

Е = Eo + Wk

(12.12)

Полная энергия Е и импульс р движущегося тела определяется следующими формулами:

(12.13)

Из (12.13) можно получить соотношение для полной энергии частицы с её импульсом и массой:

(12.14)

Безмассовые частицы, например квант электромагнитного излучения, движутся всегда со скоростью света V=c, а их импульс:

p = E/С	(12.15)
Основное уравнение релятивистской механики имеет вид:

	dP
F =		или			(12.16)
	dt
Отсюда следует и закон сохранения импульса:
		Pсист		= const

В замкнутой системе релятивистский импульс сохраняется.

50

В заключение отметим, что все формулы релятивистской механики переходят в формулы классической механики при скоростях V<<c.

												1
W = E − E		= mC2 − m		C2	= m			C2									−1			(12.16)
K	0		0				0					1−			2
														β
				2			1			2					1					2
При малых скоростях V<<С W			≈ m	C	1	+			β		−1 =						m		V
		K	O				2								2			O

т.е. при малых скоростях релятивистская механика переходит в классическую.

Ликбез: При малых значениях x справедливо приближённое равенство:

(1+ x)

α

≈1

+ αx поэтому

−

1

1

(1− β

2

≈ 1+

β

2

) 2

2

Конец ликбеза.

Справедливы также некоторые другие соотношения:

Из (12.15) и (12.12) следует:

E2 = m2C4

= m

2C4 + р2С2

(12.17)

O

P = m V =

E

V

(12.18)

C2

Все уравнения релятивистской динамики инвариантны к преобразованиям Лоренца.

12.7.Выводы по специальной теории относительности

1.Понятия время, расстояние, масса не являются абсолютными, а зависят от скорости тел.

2.Масса и энергия эквивалентны.

3.Пространство и время взаимосвязаны и образуют единое четырёхмерное пространство-время. Изменяются понятия одновременности и другие.

Мы рассмотрели частную (специальную) теорию относительности. Существует и общая теория относительности, в которой учитывается влияние гравитационного поля. Оказывается, гравитационное поле приводит к искривлению пространства.

51

Основные формулы

Название

Формула

Комментарии

dr

r - радиус-вектор,

Мгновенная скорость

V =

t – время

dt

2

d

а – численно равен

Мгновенное ускорение

dV

r

изменению скорости за

a

= dt

= dt2

единицу времени

aτ = dV dt -

тангенциальная

составляющая ускорения

Разложение ускорения

a = aτ + an

an = V2 R - нормальная

на составляющие

a =

2

+ a

2

an

τ

составляющая ускорения

R – радиус кривизны

траектории

ω = dϕ

Угловая скорость

dt

dϕ - вектор угла

Угловое ускорение

d

d

2

поворота

=

щ

=

ϕ

е

dt

dt

2

Связь между

S = R ϕ;V = R ω

S – длина дуги, ϕ - угол

поворота,

линейными

aτ = R ε;an

= ω

2

R

R – радиус окружности,

и угловыми величинами

dp

ε - угловое ускорение

F - результирующая

Второй Закон Ньютона

F =

= m a

сила,

dt

(основное уравнение

p = m V - импульс,

динамики)

m – масса материальной

точки

F12 = −F21

СилыF12 и F21

Третий Закон Ньютона

приложены к телам 1 и 2

соответственно

Закон изменения

d Pсист

Справедлив для любых

импульса для системы

= Fрезвнеш

систем материальных

материальных точек

dt

точек

n

Справедлив для

Закон сохранения

= const

замкнутых систем, (на

Рсист = ∑mi Vi

импульса

i=1

которые не действуют

внешние тела)

Элементарная работа

δA =

= FdrCosα

F - сила, dr -

перемещение,

силы

(Fdr)

α − угол между F и dr

52