Лекции по физике

Плоское движение можно представить как сумму поступательного и вращательного движения.

Можно показать, что кинетическая энергия при плоском движении равна сумме кинетических энергий поступательного движения тела со скоростью центра масс плюс кинетическая энергия вращения вокруг оси, проходящей через

центр масс:
W	=	mVC2	+	JCω2
Kллос	2		2		(8.11)

Где m – масса тела, VC – скорость центра масс, JC – момент инерции тела

относительно оси, проходящей через центр масс, ω – угловая скорость вращения тела.

Пример: Найдём кинетическую энергию обруча, массой m, катящегося без проскальзывания со скоростью V.

W	= mV 2	+ J 2ω2		= mV 2	+ mR 2V2	= mV2
K		2		2	2 R2
	2
	Кинетическая		энергия		катящегося обруча

mV2

оказалась больше, чем		.

2

Таблицу сравнения поступательного и вращательного движения смотри в конце конспекта.

Лекция 9-11. Колебательные процессы 9.1 Единый подход к колебаниям различной физической природы

Точное определение колебаний дать сложно. Объединяющим для колебаний является периодичность или приблизительная периодичность процессов.

Строго периодичным называется процесс бесконечный во времени, для которого справедливо f(t)=f(t+T), здесь Т – период.

Очевидно, что таких процессов в природе не существует, хотя бы потому, что любой процесс ограничен по времени. Поэтому в определении колебаний говорится о приблизительной периодичности процесса.

Примеры колебаний: маятник часов, приливы-отливы, переменный ток, звук, электромагнитные волны. При этом периодически изменяются различные физические величины: координаты, ток, плотность, напряжённость электрического и магнитного поля.

Самое удивительное в том, что совершенно различные с виду колебательные явления описываются одинаковыми математическими

33

уравнениями и поэтому обладают одинаковыми свойствами. Изучая колебания в механике, можно понять некоторые оптические явления и наоборот.

Советский физик А.И. Мандельштам с полным основанием утверждал, что главные открытия в физике по существу были колебательными.

Хотя мы будем рассматривать только временные колебания, повторяющиеся во времени, следует знать, что понятие колебаний распространяют и на процессы, повторяющиеся в пространстве. Это т.н. пространственные колебания.

9.2 Гармонические колебания

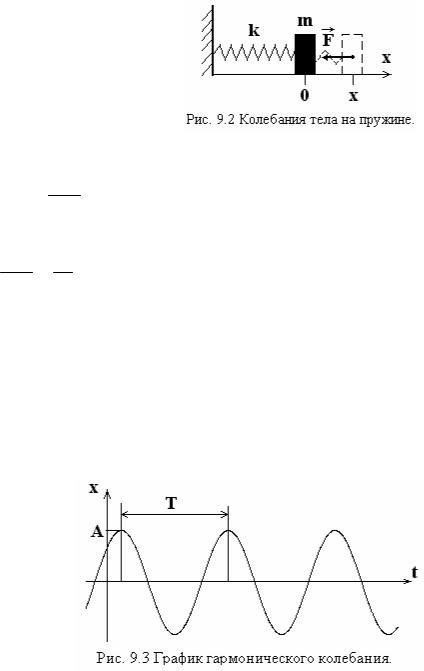
Рассмотрим колебания тела на пружине в отсутствие трения; m – масса тела, k – жёсткость пружины. На тело действует упругая возвращающая сила F=−k x, где x – смещение из положения равновесия.

Из уравнения движения m a=F получаем дифференциальное уравнение для гармонических колебаний:

m d2x = −k x
dt2
Или
d2x + k x = 0	(9.1)
dt2 m

Это обыкновенное однородное линейное дифференциальное уравнение 2- ого порядка с постоянными коэффициентами. Его решением является

гармоническое колебание, (по определению, колебания, описываемые

уравнением вида (9.2), называют гармоническими):
x=Αcos(ωt+ϕ)	(9.2)

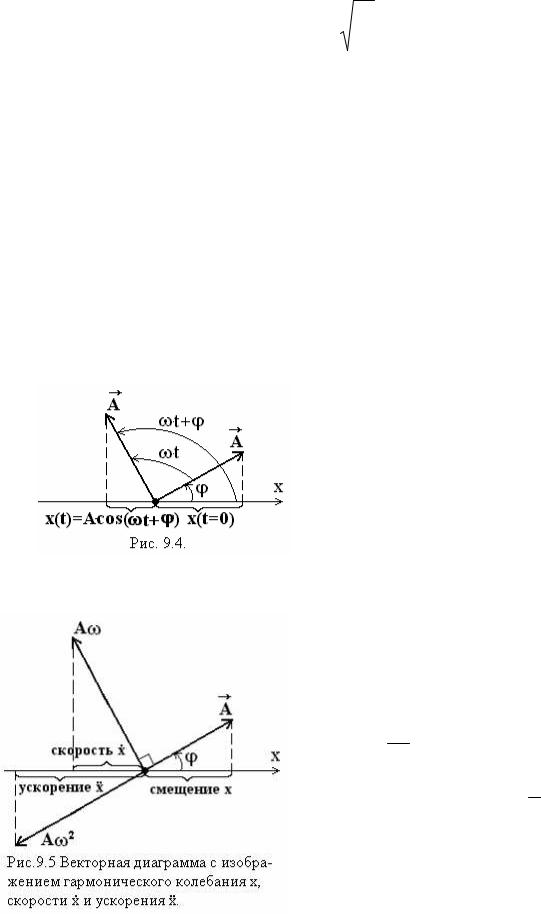
где А – амплитуда колебания, (амплитуда соответствует максимальному отклонению от положения равновесия), ω - круговая частота, (ωt+ϕ) – фаза колебания, ϕ - начальная фаза,

соответствует фазе при t=0. Далее мы убедимся, что такое же дифференциальное уравнение (9.1) и такое же решение (9.2) будет описывать огромное число колебательных процессов. Отличие будет заключаться только в коэффициенте перед переменной x. (Вместо k/m будут другие параметры

соответствующей колебательной системы).

Величины А и ϕ в (9.2) определяются начальными или граничными условиями, ω - круговая частота, определяется параметрами колебательной

34

системы: оказывается , что всегда ω2 равна коэффициенту перед x в уравнении (9.1):

	ω =	k		(9.3)
		m
	Периодом колебаний T=2π /ω	- называют отрезок		времени,
	затрачиваемый на одно полное колебание.
	Частота ν=1/Τ это число колебаний за единицу времени.
	Частота связана с круговой частотой соотношением:
	ω=2πν			(9.4)

Единица измерения [ ν ] = Гц.

Уравнение гармонических колебаний описывает бесконечное число различных физических явлений;

звук: ρ = ρocos(ωt + ϕ) - изменение плотности в точке,

свет: E = Eo cos(ωt + ϕ) - напряженность электрического поля в точке экрана.

9.3 Векторные диаграммы. Кинематика гармонических колебаний

Гармоническое колебание x=A cos(ωt+ϕ) можно представить на

векторной диаграмме в виде проекции на ось x вектора длиной А, вращающегося против часовой стрелки с угловой скоростью ω.

В момент времени t=0, фаза равна ϕ и

вектор A отклонён на угол ϕ. В моментвремени t угол увеличивается на ωt иA полный угол поворота вектора A составляет (ωt+ϕ).

Рассмотрим на векторной диаграмме смещение, скорость и ускорение гармонически колеблющейся точки.

Пусть смещение: x=Acos(ωt+ϕ), тогда скорость точки:

V = dx = −A ω sin(ω t +ϕ) = dt

= A ω cos(ω t +ϕ + π) 2

Скорость также является гармоническим колебанием с амплитудой Аω, а начальная фаза скорости равна ϕ + π/2, т.е. на π/2 больше, чем начальная фаза смещения ϕ. На векторной диаграмме

35

скорость также изображается проекцией вращающегося вектора длиной Аω, начальное положение которого дополнительно сдвинуто против часовой стрелки

на			π/2,	рис.9.5.
Ускорение точки	a =	d2x	= −Aω2cos(ωt + ϕ) = Aω2cos(ωt + ϕ + π)является
		dt2

колебанием, которое происходит в противофазе (сдвинуто по фазе на π). Амплитуда ускорения равна Аω2.

На векторной диаграмме вся тройка векторов x,V и a вращается против часовой стрелки с угловой скоростью ω (Рис. 9.5).

9.4 Комплексное представление колебаний

Колебание можно представить в комплексной форме:

x = Acos(ωt +ϕ) = Re{A ei(ωt+ϕ )}= Re{xˆ}

где комплексное колебание x€ имеет вид:

ˆ

i(ωt+ϕ )

= Ae

iϕ

e

iωt

ˆ

iωt

x = A e

= A e

Вектор

ˆ

iϕ

= Acosϕ + iAsinϕ

-

называется

комплексной

A = Ae

амплитудой.

В комплексной плоскости он изображён

вектором A под углом ϕ к действительной

оси Re. Умножение на eiωt эквивалентно

дополнительному повороту вектора A на

угол ωt. (Рис.

9.6).

Комплексная форма

эквивалентна векторной диаграмме. Обычно все операции делают в

комплексной форме с величинами типа x€ и только в конце берут действительную

часть результата (проекцию на ось Re).

9.5 Сложение (суперпозиция) скалярных колебаний и векторных колебаний одного направления

Если периодически изменяется скалярная величина, то колебание называется скалярным. Если периодически изменяется векторная величина – колебание называются векторным.

Пример скалярных колебаний - звук. При этом колебание плотности имеют

вид:

Δρ1=Acos(ωt+ϕ1) и Δρ2=Acos(ωt+ϕ2) – при сложении двух звуковых волн

Δρ= Δρ1+ Δρ2.

Пример векторных колебаний – электромагнитные волны, например свет. Напряжённость электрического поля в некоторой точке экрана можно выразить гармоническими колебаниями:

E1 = Eo1 cos(ωt + ϕ1 ) и E2 = Eo2 cos(ωt + ϕ2 )

36

При сложении двух световых волн в данной точке экрана они складываются

скалярно Е=Е1+Е2 только при условии, что колебания имеют одинаковое

направление, т.е. E1 E2 , (иначе колебания должны складываться векторно

E = E1 + E2 ).

Пусть складываются векторные колебания одного направления (или скалярные колебания), имеющие одинаковую круговую частоту (важна одинаковость частот ω1=ω2=ω):

x1=A1cos(ωt+ϕ1) и x2=A2cos(ωt+ϕ2) Тогда их суперпозиция также даёт гармоническое

колебание с некоторой амплитудой А и фазой ϕ: x=x1+x2=A1cos(ωt+ϕ1)+ A2cos(ωt+ϕ2)=Acos(ωt+ϕ)

где амплитуда и фаза результирующего колебания определяются соотношениями:

	2	2	2	+2A1A2 cos(ϕ1-ϕ2) ,	tgϕ =	A1sinϕ1	+ A	2sinϕ2
	A	=A1	+A2						(9.5)
						A1cosϕ1	+ A	2cosϕ2

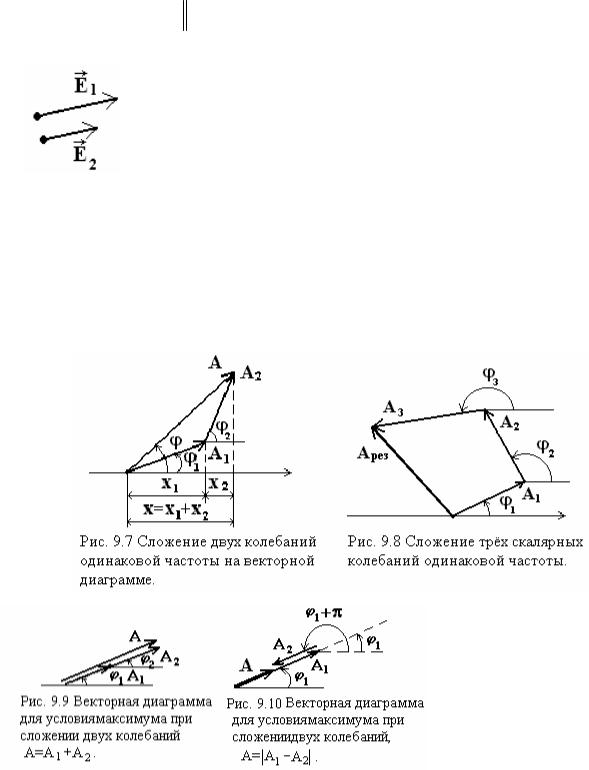
Геометрическое сложение колебаний одного направления и одинаковой частоты эквивалентно сложению векторов на векторной диаграмме, рис. 9.7. При этом результирующий

вектор А и весь треугольник вращается с частотой ω против часовой стрелки. Если складываются колебания от многих источников, то последовательно складываются все векторы. (рис. 9.8).

Частные случаи: Условия max и min при сложении колебаний: Условие max амплитуды реализуется, если ϕ1=ϕ2 (точнее ϕ1-ϕ2=2πn, n-целое). В этом случае А=А1+А2 – получим в сумме максимальную амплитуду результирующего колебания. Поэтому условие максимума имеет вид:

ϕ1-ϕ2=2πn ,

n = 0,±1,±2... (условие max) (9.6)

37

1. Условие min амплитуды реализуется, если ϕ2=ϕ1+π (точнее ϕ1-ϕ2=π+2πn, n-целое). В этом случае А=А1-А2 – получим в сумме минимальную амплитуду результирующего колебания. Поэтому условие минимума имеет вид:

ϕ1-ϕ2=π + 2πn, n = 0,±1,±2... (условие min) (9.7)

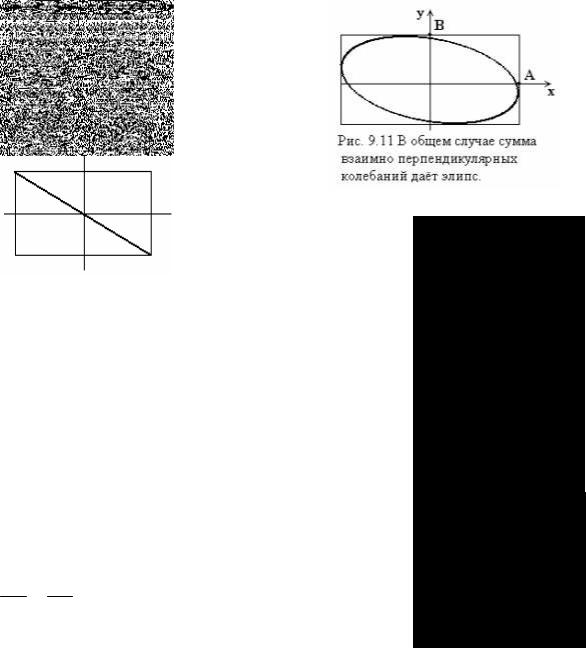
9.6 Сложение взаимно перпендикулярных колебаний, имеющих одинаковую частоту

Пусть точка смещается по оси x по закону: x=Acos(ωt+ϕ1), и одновременно по оси y по закону: y=Acos(ωt+ϕ2), т.е. происходит сложение (суперпозиция) взаимно перпендикулярных колебаний.

Исключая время t, из этих выражений можно получить уравнение траектории:

x2	+	y2	− 2	x y	cos(ϕ − ϕ			) = sin2 (ϕ − ϕ		)
A2		B2		A B		1	2	1	2

Это уравнение эллипса. Рассмотрим частные случаи:

1. Если ϕ1−ϕ2 = 0, ±2π, ±4π, …, ±2πn - то эллипс превращается в прямую, проходящую через 1 и 3 четверти;

x			y		2	y =	B	x
		−			= 0
A			B				A

2. Если ϕ1−ϕ2 = π + 2πn, где n = 0, ±1, ±2 …– прямая проходит через 2 и 4 четверти;

x			y		2	y = −	B	x
		+			= 0
A			B				A

3. При условии ϕ1−ϕ2 = π/2 + πn – эллипс, где n = 0, ±1, ±2 … главные оси эллипса совпадают с осями x и y:

x2 + y2 =1 A2 B2

3.а. Если дополнительно выполняется условие: А=В, то эллипс переходит в окружность

9.7 Фазовая плоскость, фазовые диаграммы

	ɺ		1		dx
Плоскость с абсциссой x и ординатой	x	=				называют фазовой.
	ω		ω dt

38

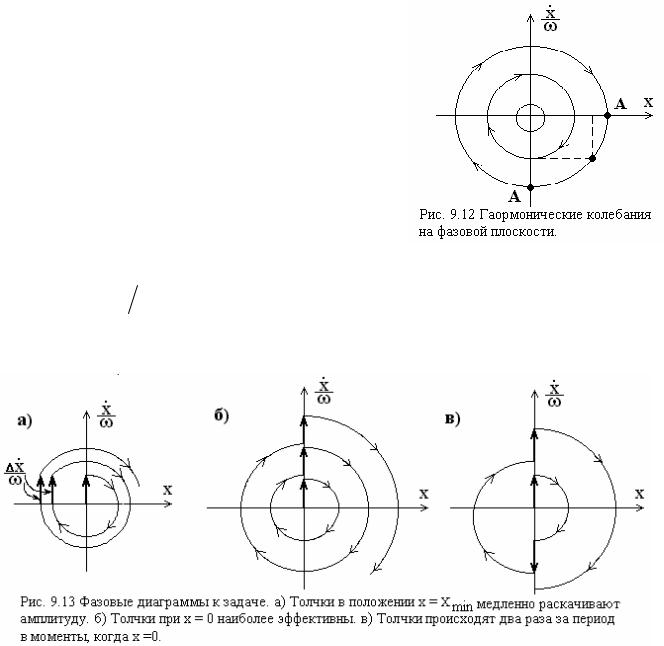
Гармоническое колебание на фазовой плоскости имеет вид точки движущейся по окружности по часовой стрелке, рис.9.12.

	x = Acos(ωt + ϕ)
		xɺ
	y =			= −Asin(ωt + ϕ)
		ω

Положение точки на фазовой диаграмме полностью характеризует состояние колебательной системы.

Задача: Как короткими толчками лучше раскачать качели?

Решение: Толчок эквивалентен тому, что тело получает дополнительный импульс и скачок скорости V ≡ xɺ .

		ɺ
На фазовой плоскости скачок скорости x приводит к сдвигу точки по оси
ординат на	ɺ	ω. Лучший результат по раскачке амплитуды получается,
	x

если точки соответствуют моменту прохождения качелей через положение равновесия x=0, рис. 9.13.

9.8Гармонические осцилляторы

9.8.1Математический маятник

Математический маятник это точечная масса на невесомой нерастяжимой нити.

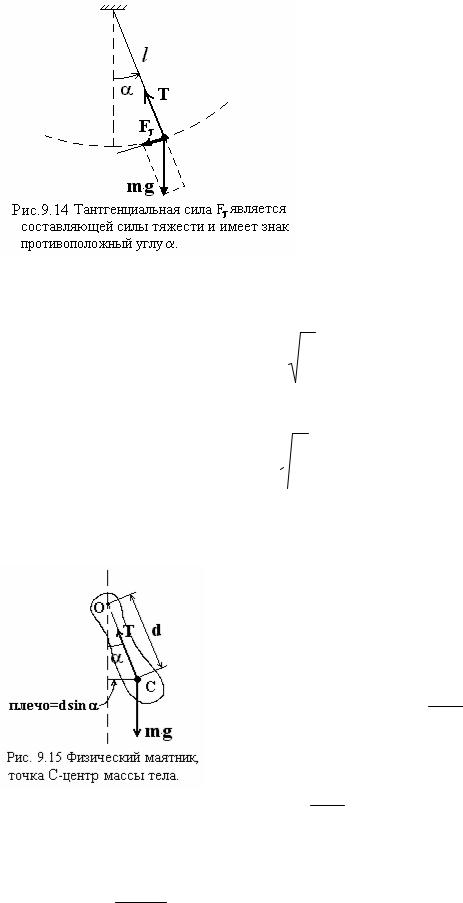
Тангенциальное ускорение аτ возникает под действием тангенциальной силы Fτ =−m g sinα ≈-m g α, рис. 9.14. (Напомним, что при малых α sinα ≈ α). С

другой стороны, аτ связано с угловым ускорением ε = d2α/dt2 соотношением:

	aτ = l ε = l	d2α	где l – длина нити.
		dt2

39

Из второго закона Ньютона m аτ = Fτ , получаем:

			m l	d2α	= −mgα	или
				dt2
d2α	+	g	α = 0			(9.10)
dt2
		l

Полученное дифференциальное уравнение аналогично уравнению (9.1). Его решением также является гармоническое колебание

α=αocos(ωt+ϕ)

(9.11)

Где квадрат круговой частоты ω2 равен коэффициенту перед переменной α в дифференциальном уравнении (9.10).

	ω =	g	(9.12)
		l

Соответственно, период колебаний математического маятника описывается формулой:

T = 2π	l	(9.13)

g

9.8.2. Физический маятник

Физический маятник это тело, колеблющееся вокруг фиксированной точки.

Момент силы М, действующий на тело, равен

F ”плечо”:

М =−m g d sinα ≈-m g d α.

Сила T, проходящая через ось вращения, момента не создаёт.

Уравнение движения: J d2α = M,

dt2

где J – момент инерции тела относительно оси,

проходящей через точку подвеса О.
J d2α + mg d α = 0	(9.14)

dt2

Данное дифференциальное уравнение имеет следующее решение:α=αocos(ωt+ϕ),

ω2 = mg d

где . Итак, для физического маятника:

J

40

ω =

mg d

,

T =

2π

= 2π

J

(9.15)

ω

mg d

J

физ

Период

физического

маятника

совпадает

с периодом математического

маятника

T

= 2π

l

, если длину математического маятника взять равной

мат

g

l =

J

.

Эта

величина

называется приведённой

длиной физического

m d

маятника.

9.8.3Пружинный маятник

Вразделе 9.2 мы получили выражение для круговой частоты и периода колебаний пружинного маятника:

	ω =			k	(9.17)
				m
T	= 2π			m	(9.18)
пруж				k

9.8.4 Колебательный контур

Простейший колебательный контур состоит из индуктивности L и параллельно подключённой ёмкости С. (Рис. 9.17).

U

=

q

-

разность

потенциалов

на

C

C

конденсаторе,

U

= −L

dI

= −L

d2q

- разность

L

dt

dt2

потенциалов на катушке.

При параллельном соединении: Uc=UL и мы

получаем: d2q + 1 q = 0

dt2 CL

Его решение: q=qocos(ωt+ϕ). Коэффициент перед переменной q равен ω2 , поэтому для колебательного контура:

	ω =		1			T =	2π	= 2π
				,					LC	(9.19)
							ω
			LC			конт

9.9 Свободные затухающие колебания. Логарифмический декремент и добротность

Часто на тело действует не только упругая сила F=-kx, но и сила сопротивления или трения FТР = −r dx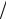dt , пропорциональная скорости тела (противоположно ей направлена).

41

Уравнение движения приобретает вид ma = −kx − r dx , или

dt

m

d2x

+ r

dx

+ kx = 0

(9.20)

dt2

dt

1. При

r

<

k

, (β<ωo), решение этого дифференциального уравнения имеет

2m

m

вид:

x = A

o

e−β tcos(ωt + ϕ)

(9.21)

Это

уравнение

свободных

затухающих

колебаний.

Здесь

параметры

А

и

ϕ определяются

начальными

условиями.

По

определению величина

β = r 2m –

называют

коэффициентом

ωo =

затухания,

k m

является

частотой свободных незатухающих

колебаний,

а

частота затухающих

колебаний определяется формулой:

				k		r		2
2		2
ω = ω o − β			=		−			(9.22)
				m		2m

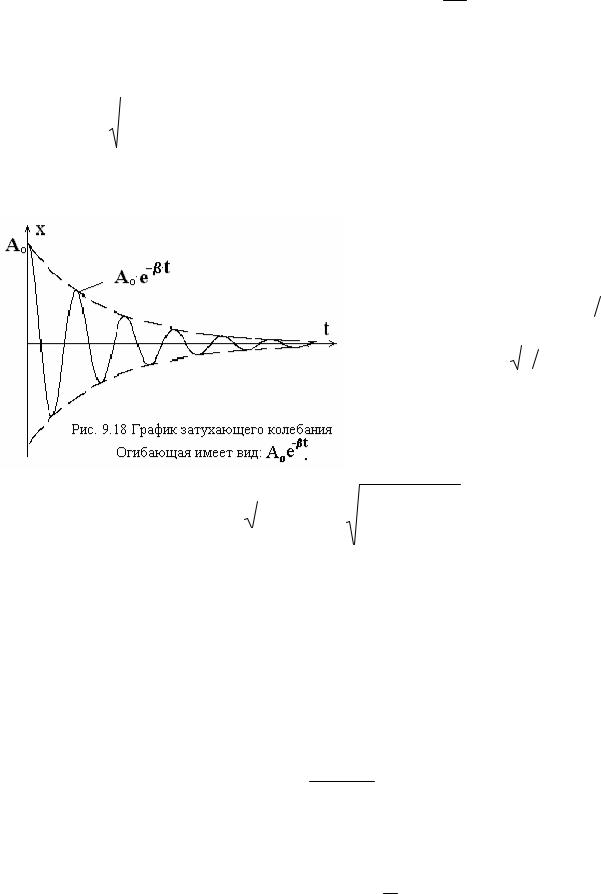
График затухающего колебания представлен на рис. 9.18. Амплитуда такого колебания убывает по закону Aoe−βt . Затухающее колебание не периодическая функция, но для него можно ввести условный период T=2π/ω.

2. При β>ωo имеем апериодическое колебание. При этом амплитуда без колебаний быстро спадает до нуля.

Логарифмическим декрементом затухания называется натуральный логарифм отношение отклонения системы в моменты времени t и t+T:

ϑ = ln x(t) = β x(t + T)

Величина 1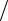ϑ равна числу колебаний (числу периодов) за которое амплитуда уменьшается в е раз.

Добротностью Q называется величина Q = ϑπ .

Чем выше добротность колебательной системы, тем медленнее затухают колебания.

42