9.4.2. Поверхностный интеграл iIрода.

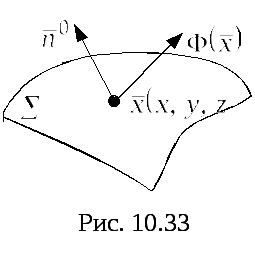
Определение 4. Пусть – гладкая ориентированная поверхность в пространстве, ориентация которой определяется единичным вектором(рис. 25). Пусть также в каждой точкеопределена векторная функция=. Поверхностный интеграл первого рода, когда подынтегральной функцией является скалярное произведение, называетсяповерхностным интегралом второго рода

.

И

ногда используется другое обозначение. Есливектор, совпадающий си по длине равный площади, то

.

П

Рис.25

оверхностный интеграл второго рода обладает всеми свойствами поверхностного интеграла первого рода: линейности, аддитивности, монотонности, а также следующим свойством. При изменении ориентации поверхности, поверхностный интеграл второго рода изменяет знак на противоположный. Действительно, пустьимеет, аимеет ориентацию, тогда

.

Запишем развернутое представление интеграла. Так как , а, где,,– углы, которые образует векторс осями координат, то

.

Согласно лемме, величины ,,– есть «приближённые» площади проекции элемента поверхностина координатные плоскостиyOz, xOz, xOy соответственно, то есть ,,, тогда

.

В

ычисление интеграла. Пусть – гладкая поверхность, заданная векторным представлением, где,. Нормаль копределяется векторным произведением касательных векторов (рис.34):

.

В

Рис.34

ыберем в областиG в качестве элементарный площадки параллелограмм со сторонами и. Тогда на поверхностиему будет соответствовать параллелограмм со сторонамии(если пренебречь кривизной поверхности). Тогда площадь элементарной площадки на поверхности будет:.

Получаем

,

где – смешанное произведение векторов. В координатной форме

. (22)

Таким образом,

. (23)

В правой части (23) стоит двойной интеграл по области G плоскости , а подынтегральная функция определена формулой (22).

Рассмотрим частный случай. Пусть область имеет явное представление. Обозначим,ии подставим в (22) и (23).

.

Если ина, то получаем

,

где – проекция нахОу.

Аналогично получаются следующие формулы. Если поверхность задана

функцией и, то

.

Если поверхность задана явно уравнением и, то

.

Пример 11. Вычислить интеграл , где – внешняя сторона параболоида , отсечённая плоскостью . (рис.35)

Решение. Заметим, что . Найдём нормаль к поверхности:

Рис.26

Рис.27

Рис.27

.

Ясно, что для единичного вектора выполняется условие:приипри. Поэтому разбиваем поверхность на две частии, описываемые уравнениямиприиприсоответственно (рис. 26).

Каждая из этих частей проектируется на плоскость в одну областьG, граница которой состоит из параболы и прямой. Сведём поверхностные интегралы поик двойным интегралам:

Используя подстановку , при, получаем

Укажем ещё один способ вычисления поверхностного интеграла второго рода через поверхность, заданную в неявном виде уравнением . Её можно рассматривать как поверхность уровняв скалярном поле, нормалькоторого направлена по градиенту в сторону возрастания С. Так как , тогда

. (24) (29)

Эта формула представляет собой поверхностный интеграл первого рода. Знак выбирается в зависимости ориентации поверхности.

П

Рис.28

ример 12. Вычислить поверхностный интеграл второго рода, если , а Σ есть внешняя поверхность параболоида, отсечённого плоскостью(рис.28).

Решение. Рассмотрим скалярное поле ,. Направление градиентаF совпадает с направлением нормали :

.

.

По формуле (24) получим

. <